位于不同高度的特殊点的高程测量方法研究
龚德书,蒋 华
(⒈南通大学建筑工程学院,江苏南通226019;2.南通大学电子信息学院,江苏南通226019)
位于不同高度的特殊点的高程测量方法研究
龚德书1,蒋 华2
(⒈南通大学建筑工程学院,江苏南通226019;2.南通大学电子信息学院,江苏南通226019)
介绍一种位于不同高度的特殊点的高程测量方法及计算公式,并推导误差分析公式,模拟位于不同高度的特殊点和不同观测角度、距离对高程测量精度的影响,从而得出一些结论。实例结果表明,该方法具有较强的实用性和可操作性,能较好地测量位于不同高度的特殊点的高程,可以满足工程测量的需要。
特殊点;高程测量;前方交会;误差分析
一、引 言
在工程测量中,常常需要测量高差较大的位于不同高度的特殊点的高程,即在其上或其铅垂线下方不能安置棱镜的点,如架空线、桥梁、烟囱、高楼大厦、高耸天线等建(构)筑物的顶端或其他特殊位置。对于特殊点的高程测量,通常需要借助于各种基线间接确定测站到特殊点的距离,如文献[1]提出了在测站上变动仪器高度的方法,但其精度有待商讨;文献[2-5]介绍了在竖直面内建立水平基线,采用竖直角前方交会的方法,但主要适用于架空线等线状地物,对其他情况适用条件有待进一步探讨;文献[5-8]介绍了在水平面内建立水平基线,采用水平角前方交会的方法,但文中给出的误差分析公式均存在不同程度的错误,还需要仔细推敲,部分结论有待商榷。基于上述情况,本文在水平面内建立水平基线,采用水平角前方交会的方法,对位于不同高度的特殊点的高程测量进行研究。主要研究了位于不同高度的特殊点的高程测量方法及计算公式,并推导了误差分析公式,模拟了位于不同高度的特殊点和不同观测角度、距离对高程测量精度的影响。最后选用实例数据验证了本文测量方法的正确性。
二、测量方法及计算公式
1.测量方法
如图1所示,设特殊点P为高程待求点,其在水平面上的投影为P',在P的一侧选择互为通视的A、B两点作为测站点,以A、B两点建立水平基线。在A、B两点上分别安置全站仪,观测水平角α=∠P'AB、β=∠ABP';竖直角 αAP、αBP;水平距离DAB;量取仪器高iA、iB。根据附近的已知水准点,用水准测量方法测量A、B两点的高程HA、HB。

图1 前方交会高程测量示意图
2.计算公式
A、B、P 3点在水平面上投影所组成的平面三角形中,应用正弦定理得

式中,γ=180°-α-β;DAP'、DBP'分别为A点、B点到P'点的距离。
利用三角高程测量计算公式,分别由A点、B点计算P点的高程

以上两式取平均值得特殊点P的高程

在使用式(3)、式(4)计算P点的高程时,因测量误差的影响,其高程不可能相等,但两式高程之差应不大于允许误差(如取3倍的高程中误差),否则应分析原因后重新观测。
三、精度分析
1.误差公式
聪明的人,要做的就是通过不断思考,慢慢地把失误降到最少 ;而愚笨的人,只要努力学习、勤于思考,收获也会越来越多。
设测量特殊点P的高程中误差为mH;水平距离DAB的距离中误差为mD;水平角α、β的测角中误差为mβ;竖直角αAP、αBP的测角中误差为mα;仪器高iA、iB的量取中误差为mi。假定高程HA、HB的测量中误差为零,根据误差传播定律,对式(5)进行全微分可得
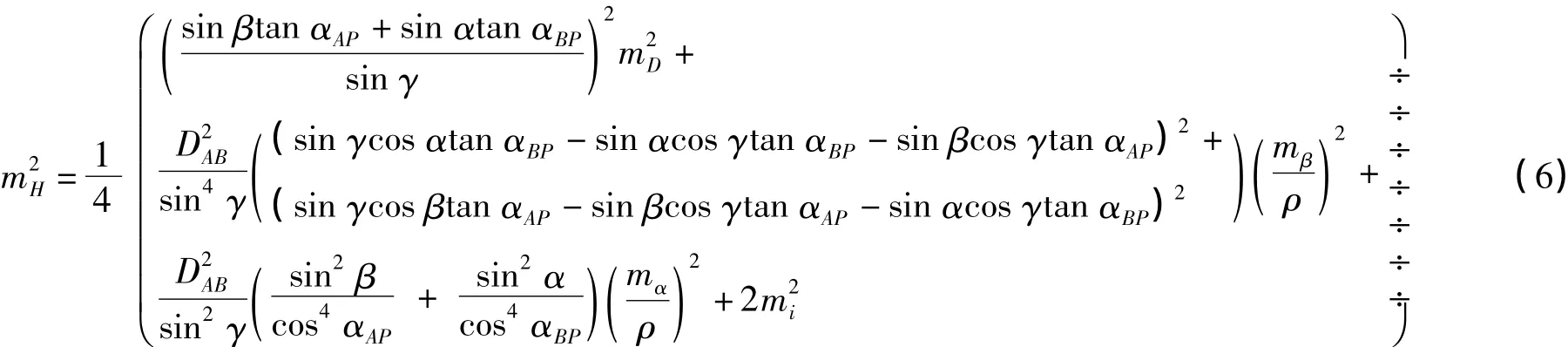
由式(6)可得出以下结论:
1)当mD、mα、mβ及mi为一定值时,mH主要取决于特殊点P的高度和P、A、B 3点所组成的立体几何图形,即hAP、hBP、DAB、α、β、αAP、αBP的大小。
2)当γ=90°时,mH受水平距离和水平角测量误差的影响较小。
3)当hAP≅hBP且α≅β≅55°、γ≅70°时,mH受水平角测量误差的影响最小。
4)当αAP=αBP=45°时,mH受竖直角测量误差的影响最小。
2.精度分析
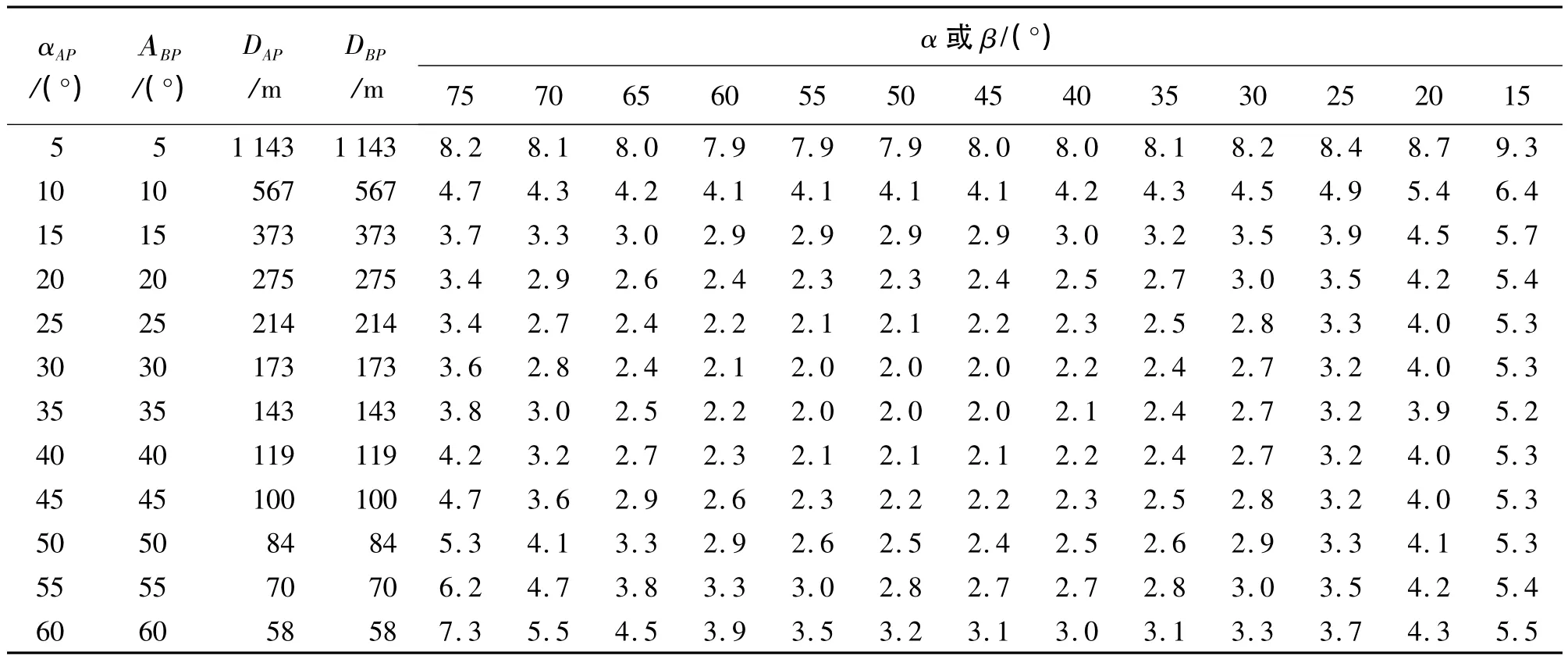
表1 高度为100 m的高程测量精度 mm
从表1中可得出以下结论:
1)当竖直角在30°~40°时,高程中误差最小为±2.0 mm。
2)当竖直角在25°以下或40°以上时,高程中误差逐渐增大。
3)当水平角为45°~60°(交会角为60°~90°)时,高程中误差较小。
4)当水平角为25°~40°或65°~75°(交会角为100°~130°或30°~50°)时,高程中误差其次。
5)当水平角为15°~20°(交会角为140°~150°)时,高程中误差较大。
另对模拟计算结果分析还可以得到:
1)当高度增大时,适当增大竖直角但不大于45°,将减小竖直角观测误差对高程中误差的影响。
2)当高度增大时,任意减小竖直角,将明显增大竖直角观测误差对高程中误差的影响。
综上所述,实际测量时应估计特殊点的高度及周围地形情况,尽可能选择竖直角为30°~45°、水平角为45°~60°(交会角为60°~90°)、水平距离为高度的1.0~1.5倍的立体几何图形,以提高高程测量的精度。
四、实例分析
为了验证本测量方法的正确性,使用尼康(Nikon DTM-352C)全站仪,仪器标称精度为一测回方向观测中误差为±2″,距离测量精度为±(2 mm +2×10-6D)。首先,选择有代表性的高度约为50 m、100 m、200 m的3幢建筑物,在上面选择观测目标点P,在目标点上直接安置棱镜,并参考表1选择对应的竖直角以提高测量精度;其次,在地面上根据地形条件概略选择水平基线方向,用全站仪照准目标点P并读取竖直角,大致测量目标点与水平基线方向的水平夹角,移动全站仪尽可能使竖直角不小于选择的竖直角,水平夹角在45°~60°之间,确定A点;再次,用与A点相同的方法确定B点,并使A、B两点与P点距离大致相等,使A、B两点距离接近并大于目标高度;最后,按照本测量方法对角度、水平距离各观测6个测回,不同方向量取仪器高3次,如表2所示。同时在A、B两测站上,用光电测距三角高程测量方法测量P点的斜距6个测回并计算高差,计算结果如表3所示。

表2 观测成果表

表3 计算结果比较表
五、结束语
1)对位于不同高度的特殊点进行高程测量时,应根据文中精度分析的结论和地形情况,选择有利的立体几何图形,尽可能使A、B两点与P点构成等腰三角形,以提高高程测量的精度。
2)当特殊点的高度增减时,视高程测量的精度要求,宜适当增减测量角度和水平距离的测回数,以提高测量工作效率,确保测量成果的质量。
3)在测站观测结束时,应及时进行测站检查,避免各种不必要的测量错误的发生。检查时,根据高程测量的精度要求,各测回角度、水平距离之差应不大于2倍或3倍的测角、测距中误差,若超限应分析原因及时重测。
4)若要对特殊点进行悬高测量,可按本文测量方法先求得特殊点的高程,再求其对应的铅垂线与地面的交点高程、或求建(构)筑物的室内地平标高,两高程之差就是特殊点的悬高。
[1] 徐汉涛.精确悬高测量方法的探讨[J].测绘通报,2004(6):65-66.
[2] 郭宗河.悬高测量及其改进[J].测绘工程,1999,8(2):62-64.
[3] 谭旭.特殊情况下悬高测量方法的探讨[J].城市勘察,2002(3):1-4.
[4] 郑定让.精确悬高测量[J].测绘通报,2002(6): 37-38.
[5] 奚毓敏.不可到达点高程测量方法研究[J].电力勘测设计,2006(6):25-28.
[6] 刘庆金.特殊悬高之测量方法[J].测绘通报,2006 (3):43-45.
[7] 梁建昌,何娟霞,杨国范.前方交会高程测量[J].铁道勘察,2005,31(2):1-2.
[8] 杜文举.关于建筑物塔顶悬高测量的研究[J].四川建筑科学研究,2010(1):277-280.
[9] 顾孝烈,鲍峰,程效军.测量学[M].上海:同济大学出版社,2006:136-158.
Study on Elevation Measurement Method of Paticular Points in Different Height
GONG Deshu,JIANG Hua
0494-0911(2011)06-0008-03
P216
B
2010-08-27
江苏省南通市应用研究计划资助项目(K2008015)
龚德书(1962—),男,江苏常州人,硕士,高级工程师,主要研究方向为工程测量。

