基于VaR模型的证券投资组合风险管理
□文/张 利 胡 铂
基于VaR模型的证券投资组合风险管理
□文/张 利 胡 铂
本文在介绍VaR基本概念的基础上,着重分析VaR的三种获取方法,并以沪深300指数为样本,对VaR方法在我国证券市场上的应用进行实证研究。
证券市场;风险管理;VaR
20世纪七十年代以来,随着全球经济活动的日趋国际化,金融创新尤其是金融衍生工具的迅猛发展,使得金融市场的波动性日益加剧,金融风险不断加大。日趋严重的金融风险不仅影响了微观经济主体的正常运营,而且还对整个金融与经济体系的稳定性构成了威胁。为了有效地控制和降低金融风险,各种风险管理方法相继出现。20世纪八十年代末,JP摩根的风险管理人员研发出一种能够度量不同交易、不同业务部门的市场风险,并将这些风险体现为一个数值的风险度量方法,这就是VaR方法。随着VaR技术的日渐成熟,VaR方法得到了世界各金融机构及金融监管机构的广泛认可和支持,巴塞尔委员会允许金融机构采用标准化方法和内部模型法来度量市场风险,其中就是以VaR作为内部模型的核心技术。
一、VaR概述
(一)VaR的定义。VaR(Value at Risk),中文可译为受险价值、在险价值、风险价值等,它是指在一定置信水平和一定持有期内,某一金融资产或组合在正常的市场条件下所面临的最大损失额。更严格地说,VaR描述了在一定的持有期内收益和损失的预期分布的分位数。用数学公式可以表示为:
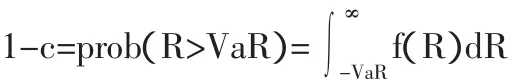
其中,1-c代表所选举的置信水平,R代表损益。
假设某公司交易的有价证券某日置信度为95%的日VaR值为100万元,根据VaR的定义,它是指在未来24小时内该有价证券在正常的市场条件下,发生大于100万元亏损的可能性为5%。
(二)VaR方法的优点
1、VaR方法是建立在概率论和数理统计的基础之上的,为全面综合地度量市场风险提供了规范的计量技术,它摒弃了主观判断的随意性,能够更加准确地计量金融机构所面临的风险状况,不仅具有很强的科学性,同时又表现出方法操作上的简便性。
2、VaR方法为人们提供了研究和管理金融风险的统一框架,VaR适用于衡量包括利率风险、汇率风险、股票价格风险以及商品价格风险、衍生金融风险在内的各种市场风险,金融机构可以定期地计算VaR值以概括反映整个金融机构的风险状况,这有利于金融机构对风险进行统一的管理,也使得风险度量的结果具有可比性,对金融市场的稳定和现代金融风险管理的发展具有重要意义。
3、VaR方法不像以往的风险管理方法只是在事后衡量投资组合风险的大小,它可以在事前计算投资组合的风险,这样投资者就可以运用VaR的方法,动态地评估和计量所持有的资产组合的风险,选择在相同的风险条件下能够带来最大收益的组合,以分散和规避风险,提高运作效率和资产收益。
(三)VaR方法的缺陷
1、VaR方法没有考虑尾部风险。本质上,VaR只是告诉我们在特定分布中对应一定置信水平的分位数是多少,并不能告诉我们分位数左侧的分布状况,即所谓的左尾损失,这就是VaR尾部损失测量的非充分性。例如,假设对应99%置信水平下的日VaR为1,000万元,即未来还有1%的可能性会出现最大损失超过1,000万元的情况,如果这种情况发生,具体会损失多少,这可能是人们更为关注的问题,因为这种小概率事件一旦发生,将会带来灾难性的后果。
2、VaR方法可能存在数据不充分或者失真的风险。VaR分析方法是依赖于历史数据的。但是,许多市场由于历史较短、市场有效性不高等原因,可能不存在充分、真实的可用数据。
3、VaR方法还可能存在模型风险。
VaR方法的运用建立在大量的模型基础之上,因此模型的选择、操作及参数估计方面如果出现错误,将给VaR的计算带来风险,也使得VaR不能很好地度量金融风险。
二、VaR的获取方法
计算VaR的关键在于确定证券或组合的未来损益的统计分布或概率密度函数,但是直接获取未来损益的分布是几乎不可能的事,因此,VaR的获取通常要经过下述分解过程:第一步,识别市场风险的因子,将资产表示为市场因子的函数,这一过程通常称为映射;第二步,预测市场因子的波动性;第三步,根据市场因子的波动估计资产的价值变化及其概率分布,这一过程也成为盯市;第四步,根据给定的置信水平和持有期,计算得出VaR。
根据对风险因子及其与资产价值之间关系的不同处理方法,可以将VaR的获取方法分为三类:
(一)历史模拟法。历史模拟法是建立在历史可以复制未来、历史数据可获得且完整有效的隐含前提下,利用历史数据集,将过去已经实现的收益率分布或市场变量分布应用于目前的投资或组合,据此模拟下一个时期该投资或组合可能面临的收益分布,给定置信水平和持有期,就可以计算出VaR。
例如,将100万元投资于工商银行的股票,根据以下步骤可以求出99%置信水平下1天的VaR值。第一步:获取收益的时间序列。样本数据选择2008~2009年每个交易日的收盘价,共482个数据,然后根据公式R=(Pt-Pt-1)/Pt-1计算出每日简单收益率,生成一个新的时间序列。第二步:在EXCEL中将序列中的数据按照升序排列,找到对应的第482×1%=4.82个数据(谨慎起见,使用第4个数据),即-8.29%,于是可得,VaR=100×8.29%=8.29万元。
(二)蒙特卡罗模拟法。蒙特卡罗模拟法的基本思路是假设资产价格或市场变量的变化服从于某个随机过程,通过模拟该随机过程,就可以得出在给定时间点上投资组合的价格或市场变量的估计值。不断重复该模拟过程,就可以得到一系列估计值。如果重复的次数足够多,模拟出的估计值最终将会收敛于“真实的”组合价值。以此为基础,就可以进一步估计出组合“真实的”风险价值。
蒙特卡罗模拟法的主要步骤是:第一步,为变量选择一个随机模型,确定模型参数,以模拟价格变化的时间路径。第二步,产生一个虚拟的随机变量系列εi,i=1,2,…,n,由此计算出价格序列。第三步,根据特定的价格序列计算目标期末的资产价值,尽可能多地重复第二、第三步,如10,000次,就可以得到一个价值分布。第四步,给定置信水平1-C,通过分位数就可以计算出VaR。
(三)方差-协方差法。方差-协方差法的基本思路是:首先假定要考察的随机变量服从于某种参数分布,如正态分布、泊松分布等,然后借助于分布参数,如均值、方差等直接计算出VaR。
以正态分布为例,方差-协方差法的基本步骤是:假设资产收益率服从于一般正态分布R=f(r)~N(μ,σ2),然后借助于正态化转换,转换成标准正态分布Φ(ε)~N(0,1):
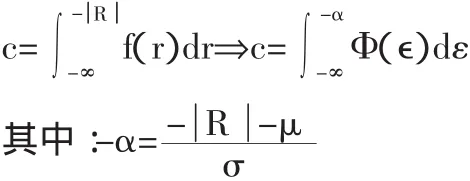
三、VaR方法在我国证券市场风险管理中的实证分析
沪深300指数选取了沪深两市300只A股作为样本,其中沪市179只,深市121只。沪深300指数样本覆盖了沪深市场60%左右的市值,具有良好的市场代表性,能够反映我国证券市场的概貌和运行状况,是反映沪深两个市场整体走势的“晴雨表”。因此,本文选取沪深300指数作为本文的研究对象。本文选取了2008年12月1日至2010年12月1日的沪深300指数每日的收盘价作为样本,样本数为484。下面,分别运用历史模拟法、蒙特卡罗模拟法和方差—协方差法计算价值为100万元的沪深300指数投资在99%的置信水平下的单日VaR值。
(一)历史模拟法。根据历史模拟法的基本原理,进行以下的计算步骤:
1、由原始样本数据计算出每日的简单收益率,公式为:简单收益率=(Pt-Pt-1)/Pt-1。
2、在 EXCEL 中将生成的简单收益率按照升序排列。
3、找到对应的第 484×1%=4.84个数据(谨慎起见,用第4个数据),即-5.51%。
4、计算可得:VaR=100×5.51%=5.51万元。
(二)蒙特卡罗模拟法
1、利用EVIEWS软件中的单位根检验(ADF检验)来判断股票价格序列的平稳性,由结果可知DF=-1.860199,大于10%水平下的临界值,因此可知该序列是非平稳的。
2、利用EVIEWS软件中的相关性检验来判断序列的自相关性。选择价格序列的一阶差分(△P=Pt-Pt-1)和30天的滞后期。由结果可知,沪深300指数收盘价的一阶差分序列不具有相关性,即其分布具有独立性。我们可以得出如下结论,沪深300指数的收盘价格服从随机游走,即Pt=Pt-1+εt。
3、利用EXCEL软件做蒙特卡罗模拟,模拟次数为10,000次,首先产生10,000个随机数,考虑到股市涨跌停板的限制,以样本期最后一天价格3136.99为起点,即价格在下一天的波动范围为(-313699313699),故随机数的函数式为:Randbetween(-313699313699),生成的数即为我们需要的股价随机变动数εt。然后获取模拟价格序列:模拟价格=P0+随机数/1000。再将模拟后的价格按照升序重新排列,找出对应99%的分位数,即10000×1%=100个交易日所对应的数值:2,829.944,于是可计算出 VaR=100×(3136.99-2829.944)÷3136.99=9.79万元。
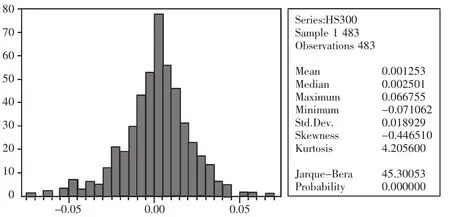
图1 简单收益率分布
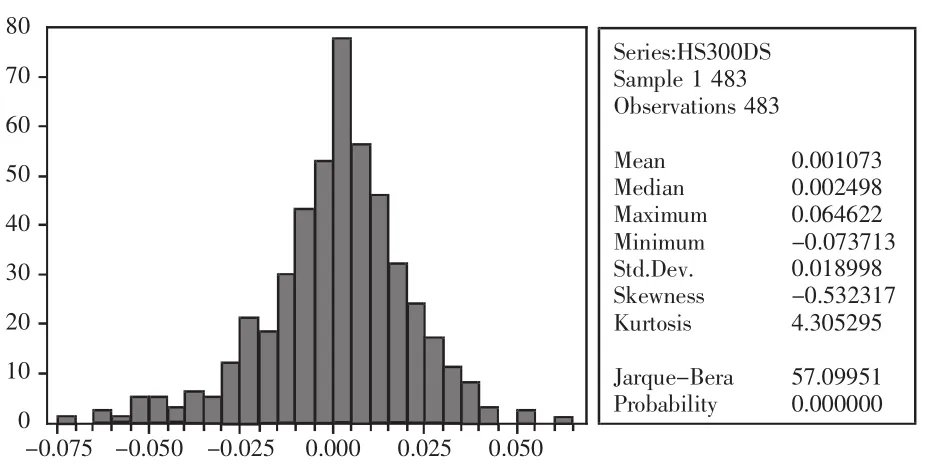
图2 对数收益率分布
(三)方差-协方差法
1、利用EVIEWS软件对样本数据进行处理,分别获取简单收益率和对数收益率的分布图。(图1、图2)标准正态分布的偏度为0,峰度为3,所有偏度非0的分布曲线都是偏斜的,峰度大于3的分布曲线则是厚尾的。由输出结果可知,二者均呈现出“尖峰厚尾”的特征。相对而言,对数收益率更接近于正态分布。
2、根据VaR的计算公式,可求得VaR=2.33×0.018998×100=4.43 万元。
四、结束语
我国的金融市场还是一个处于发展中的新兴市场,在我国金融市场和金融机构快速融入金融自由化和全球化趋势的过程中,随着金融创新的蓬勃发展,市场风险必将随着金融市场的发展而逐渐加大。将VaR的方法引入我国,不仅能够为金融机构和投资者提供一种有效的市场风险管理工具,而且能够为中央银行、证监会等金融监管部门提供一个风险管理的标准,有助于我国金融机构内部风险管理和外部监管技术跟上世界金融发展的潮流,对于我国的金融风险管理技术来说,具有重要的意义。
[1]陈燕玲.金融风险管理[M].安徽大学出版社,2008.
[2]王春峰.金融市场风险管理[M].天津大学出版社,2001.
[3]陈忠阳.金融风险分析与管理研究[M].中国人民大学出版社,2002.
[4]刘宏攀.VaR方法在我国金融风险管理中的应用研究 [D].安徽农业大学,2009.
F83
A
(作者单位:安徽大学经济学院)

