来流条件对热流组分扩散项影响效应分析

苗文博，程晓丽，艾邦成

(中国航天空气动力技术研究院，北京 100074)

0 引言

未来高超声速飞行器普遍具有高空以及高飞行马赫数的特点，此时流动的热非平衡特性也非常突出。非平衡效应会对流动产生较大的影响，它会改变激波后和壁面附近的温度以及组分分布。高马赫数状态时，激波后温度可达6000K～10000K，甚至10000K以上，氧分子、氮分子开始离解并伴随置换反应和电离反应进行，流场中原子和离子在到达壁面时会发生表面催化复合反应释放热量，这部分热量是由组分浓度梯度决定的，一般也称之为热流的组分扩散项。当流场中原子在壁面处的复合比例比较高时，壁面的催化复合放热不可忽略，称之为壁面催化效应。Sebo D.E.［1］发现多级再入轨道器要比普通再入受到更高的热流加热，认为壁面催化条件是产生这种热流差异的重要因素。Papadopoulos P.［2］，N.E.Afonina［3］通过数值模拟火星再入飞行发现不同壁面催化条件热流相差1倍还多。

壁面催化的概念很早就为人们所关注，Goulard R.J.［4］首先对比了几种典型金属和氧化物材料的壁面催化复合系数并通过试验给出了这几种材料对于氧原子的复合催化系数的大致数值。Inger G.R.［5－6］发现除了受材料的表面物理化学特性影响外，壁面温度是影响壁面催化能力的一个重要因素，并给出了关于某碳基材料的壁面催化复合系数随温度的拟合关系式。一般认为原子在壁面上主要发生以下两种类型的复合过程［7］:1)自由原子撞上吸附原子复合成气体分子(Eley-Rideal复合模型);2)壁面上吸附原子相遇复合成气体分子(Langmuir-Hinshelwood复合模型)。

在数值模拟研究中，通常建立以下三种壁面催化条件来模拟原子在壁面处的复合，分别是完全催化壁、完全非催化壁和有限催化壁，并使用壁面分子复合系数来表征催化能力的强弱。这一参数只能通过材料表面复合试验来获得，存在较高的实现成本和难度。因此，简化的壁面催化模型——完全催化壁和非催化壁是最常用的壁面催化条件。一般的存在以下共识，壁面完全催化壁所得热流要大于有限催化壁所得热流，有限催化壁所得热流大于非催化壁所得热流。在实际应用中，这种不同壁面催化模型之间的差异受诸多因素影响，需要选取适当的参数来表征这种差异。基于这一认识，本文通过分析典型来流状态下完全催化壁与非催化壁的热流差异来研究壁面催化条件的影响效应。并通过对比不同高度和马赫数的飞行状态，研究了来流条件与热流组分扩散项的相关性。

化学动力学模型和多温度模型的建立是非平衡流研究的一个重要内容，Park［8－9］、Dunn ＆ Kang［10］基于理论和试验研究提出了各自的化学动力学模型，能够准确地描述高温条件下的化学反应过程。7组分模型较多应用于近空间飞行条件，11组分模型或者23组分模型主要应用于再入飞行器研究［11］。本文选取了Park的7组分反应模型，利用精度较高的 AUSM+-up格式［12］求解了简单球锥外形的非平衡流场。来流状态选取RAM-CII［13］飞行试验状态，外形为头部半径为0.1524m，半锥角9°的球锥外形。

1 控制方程

以三维情形为例，在所研究的控制体积内，将含化学反应源项的基本方程以积分形式表示如下:

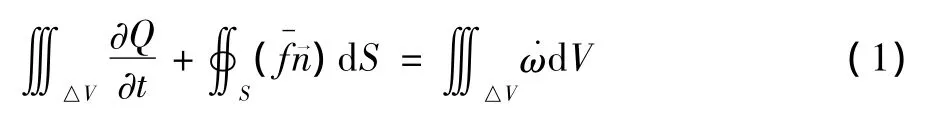
此处Q是基本守恒量，六面体控制体△V的体积为Ω。假设控制体中心标为(I，J，K)，左面中心标为(i，J，K)，右面中心标为(i+1，J，K)，以此类推。其中大写字母I表征单元体中心信息，小写字母i表征控制体面元中心信息。积分方程离散如下:

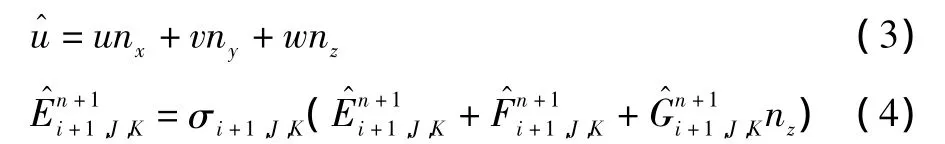
E，F，G 为原始通量表达式，σi+1，J，K为所在面面积，(nx，ny，nz)为该面法向量。

2 数值格式

AUSM格式的主要思想是认为流场在传播中存在对流影响与声波影响，为了分别考虑两个过程，将无粘项分为对流项和压力项进行处理，基于马赫数对两者分别进行特征分裂，是适用于化学反应流求解的一类高精度格式。AUSM+-up是该类格式的最新改进型，它在构造界面马赫数时引入压力耗散机制，在构造界面压力时引入速度耗散机制，在低速流动区域抑制数值震荡。下面给出其通量表达式。仅以项为例说明。

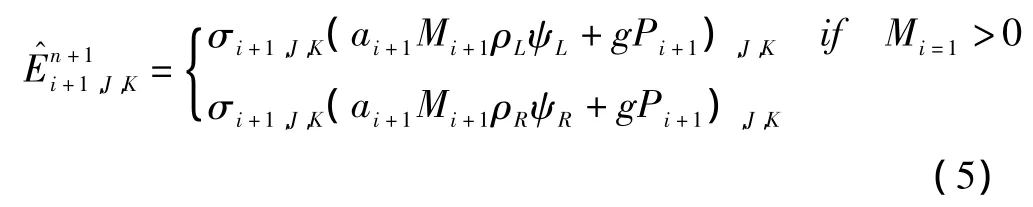
其中，ψ =(ci，u，v，w，H，eV)，g=(ci，nx，ny，nz，0，0)，界面马赫数以及压力定义见文献［12］。

3 定解条件

本文使用了Park的有限速率7组元6反应模型，各组分为 N，O，N2，O2，NO，NO+，e。选用Park的双温度模型，使用平动温度T表征平动以及转动能，使用振动温度Tv表征分子振动能以及粒子电子激发能。化学反应特征温度按照C.Park的设置给定［14］。

本文对三种壁面催化条件进行了数值模拟。根据Fick定律，有限催化壁条件满足公式(kiρCi)w=［ρDi是各组分催化复合速率，α是各组分的壁面复合系数，定义为壁面复合原子数与到达壁面原子数之比。对于有限催化壁，本文仅考虑了O和N在壁面处的复合，并且认为O和N具有相同的壁面复合系数α=0.03。

4 算例验证

为验证算法可靠性，选取J.Muylaret(1992)文献［15］引用的飞行试验数据为验证对象。几何外形为头部半径175mm，半锥角4.6°长约2m的尖锥。来流马赫数13，来流温度T=265K，来流压力P=53Pa，壁面温度取飞行试验驻点温度Tw=343K。进行了完全催化壁、非催化壁的热流与飞行试验热流的对比。图1给出了本文完全催化壁、非催化壁热流结果与飞行试验数据的对比，在驻点高热流区完全催化壁热流比非催化壁热流大30%左右，后部低热流区完全催化壁热流比非催化壁热流大30%－40%，飞行试验数据基本介于两者之间。证明本程序具有较好的非平衡数值模拟能力，可以满足热环境模拟要求。

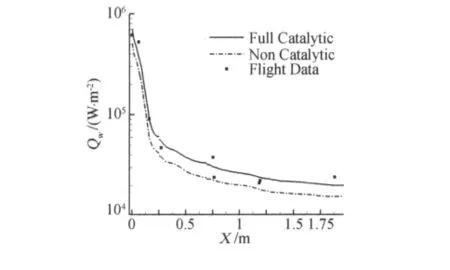
图1 热流对比Fig.1 Heat-flux along the axial direction

5 结果及分析

本文选择RAM-CII的外形为研究对象，研究了不同壁面催化条件时的热流预测差异，分析了不同壁面催化条件对热环境预测的影响，研究了来流参数对热流组分扩散项的影响。计算模型为球头半径r=0.1524m，半锥角9°，后部长度0.3m的球锥。

首先针对 M=25.9，H=71km，Tw=1500K 的典型飞行状态对比分析了三种壁面催化条件对热流预测的影响。此时的自由流速度约为7650km/s，流动的非平衡特性非常强。图2给出了三种壁面催化条件下的表面热流对比以及热流的组分扩散项对比和热传导项对比，由图可以看出不同壁面催化条件之间的差异主要体现在热流的组分扩散项部分，不同壁面催化条件时热流的热传导项贡献相差不大，在2%之内。由此可知，在固定壁温的前提下，原子的壁面催化复合过程对流场的影响非常微弱，主要影响壁面热流分布。

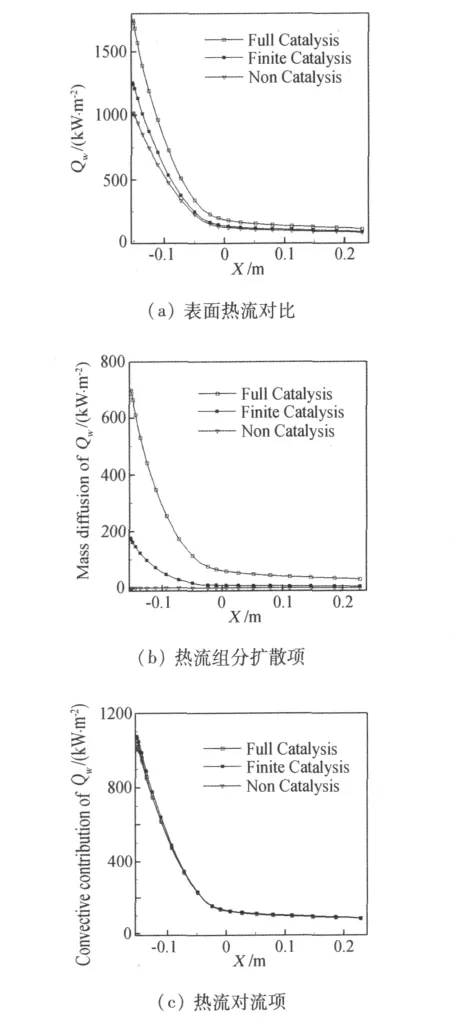
图2 不同壁面催化条件下热流对比Fig.2 Heat-flux of different catalytic conditions

因此，可以通过评估完全催化壁条件下组分扩散项热流部分所占比例来初步估计真实热流值的大小。从而避免需要通过试验获得真实条件下壁面催化复合系数的困难。图3给出了同样高度条件H=71km，马赫数分别为15、20、25.9时的热流组分扩散项与总热流的对比。可以看出在当前高度下，随着马赫数增大，热流组分扩散项在总热流中所占比例越来越高。图4给出了马赫数M=20，高度分别为71、61、51km时的热流组分扩散项与总热流的对比。可以看出当马赫数不变，随着高度增高热流组分扩散项在总热流中所占比例也越来越高。表1给出了马赫数以及高度参数对于热流组分扩散项比例的影响关系。对于高超声速流动来说，马赫数越高激波后温度就越高，分子振动离解就越容易，气体化学反应进行的越剧烈，同时随着高度增高，空气密度降低，这又减弱了气体分子通过碰撞完成能量交换的可能性，化学反应相应变弱。

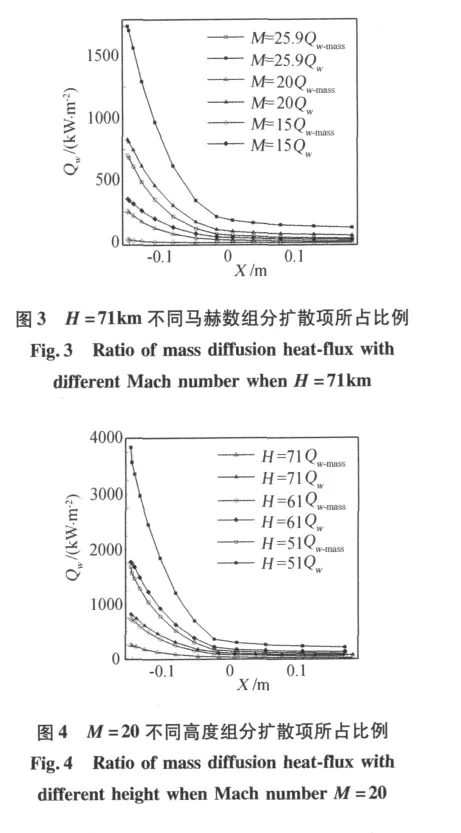
表1 马赫数和高度对热流组分扩散项的影响(单位:kW/m2)Table 1 Effects of height and Mach number on mass diffusion heat-flux(unit:kW/m2)

6 结论

针对高超声速热化学非平衡热环境预测问题，以RAM-CII飞行试验模型为参考，本文研究了壁面催化条件对热环境预测的影响以及来流条件与热流组分扩散项的关系。研究发现:完全催化壁时组分扩散项热流所占比率表征了壁面催化效应的强弱;在同一高度下，随着马赫数升高热流组分扩散项越来越显著，而马赫数相同时，随着高度增高热流组分扩散项所占比例越来越小，主要原因在于当地化学反应进行程度不同。

［1］SEBO D E.Heating effects of multiple skip reentry trajectories［R］.The Aerospace Corporation，Report No.ATR －9 I(6822)－ l，El Segundo，California，May 1991.

［2］PAPADOPOULOS P.Aero-thermal heating simulations with surface catalysis for the Mars 2001 aerospace mission［R］.AIAA 97－0473.

［3］AFONINA N E，GROMOV V G ＆ KOVALEV V L.Catalysis modeling for thermal protection systems of vehicles entering into martian atmosphere［R］.AIAA01 －2832.

［4］GOULARD R J.On catalytic recombination rates in hypersonic stagnation on heat transfer［J］.Jet Propulsion，1958，28(11):737－745.

［5］INGER G R.Correlation of surface temperature effect on nonequilibrium heat transfer［J］.ARS Jour.1962，32:1743－44.

［6］INGER G R.Non-equilibrium hypersonic stagnation flow with arbitrary surface catalycity including low Reynolds number effects［J］.Int.Jour.of Heat and Mass Transfer，1966，9:755－772.

［7］KUROTAKI T.Construction of catalytic model on SiO2-based surface and application to real trajectory［A］.34th AIAA Thermophysics conference［C］.19 －22 June 2000/Denver CO，2000－2366.

［8］PARK，CHUH.Assessment of two-temperature kinetic model for ionizing air［R］.AIAA －87－1574，June 1987.

［9］PARK CHUL.Two-temperature interpretation of dissociation rate data for N2and O2［R］.AIAA －88－0458，Jan.1988.

［10］DUNN，MICHAEL G and KANG SANG-WOOK.Theoretical and experimental studies of reentry plasmas［R］.NASACR－2232，1973.

［11］ROOP N GUPTA，JERROLD M YOS.A review of reaction rates and thermodynamic and transport properties for the 11-species air model for chemical and thermal non-equilibrium calculations to 30000K［R］.NASA-TM-101528，February 1989.

［12］MENG-SING LIOU.A further development of the AUSM+scheme towards robust and accurate solutions for all speeds［R］.AIAA Paper 2003－4116.

［13］CANDLER G V，MACCORMACK R W.The computation of hypersonic ionized flows in chemical and thermal non-equilibrium［R］.AIAA 1988－0511.

［14］PETER A GNOFFO，ROOP N GUPTA ＆ JUDY L SHINN.Conservation equations and physical models for hypersonic air flows in thermal and chemical equilibrium［R］.NASA TP－2867.

［15］MUYLARET J，WALPOT L，HAUSER J.Standard model testing in the European high enthalpy facility F4 and extrapolation to flight［R］.AIAA 92 －3905.