国际油价波动与中国成品油价格风险研究

沈沛龙,邢通政

(山西财经大学 a.财政金融学院;b.应用经济研究院,山西太原 030006)

国际油价波动与中国成品油价格风险研究

沈沛龙a,b,邢通政a

(山西财经大学 a.财政金融学院;b.应用经济研究院,山西太原 030006)

文章以扰动项为正态分布的 GARCH模型研究了Brent、Dubai和Minas原油市场的价格波动风险,以Kupiec的失败频率检验法检验模型的有效性,结果表明,模型能够刻画考察期的原油收益率波动特征,也能较好地度量上述 3个原油市场的价格风险。由于中国成品油定价过程中参照 Brent、Dubai和Minas原油市场,文章对 3个原油市场的历史数据拟合结果进行了相关性分析,通过组合波动最小原理得出 3地市场的权重比为 0.238 9∶0.575 9∶0.185 2时,中国成品油用油成本的波动率达到最小值。通过蒙特卡罗模拟验证了这一结果,实证表明在 75美元/桶的国际油价水平下,置信水平取 95%,使用最优权重能够减少用油成本波动 0.16～0.17美元/桶。

成品油;国际油价;GARCH模型;价格风险

随着经济社会的快速发展,中国的石油消耗量日益增加,且对外依存度不断提高,2008年依存度攀升到 47.95%,导致国内用油成本与国际原油价格越来越密切相关,国际油价的剧烈波动加剧了中国经济的运行风险。出于维护国内经济、政治稳定的考虑,国家政策性地屏蔽了国际油价波动对国内油价的影响,使中国成品油价格长期与国际油价脱节,也使得成品油的定价成为一个备受社会各界关注的问题。2008年 12月以前国内成品油定价采用“市场化指导、政府定夺”的原则,国家发改委参照新加坡、鹿特丹、纽约三地市场成品油价格调整国内成品油价格。但在实际操作中,油价调整过于僵化,造成了价格扭曲,成品油价格不能真实反映中国成品油的成本和需求,这不仅给国家财政带来了沉重的负担,而且影响到油品消费负担的公平性以及经济的健康发展。长远来看,中国成品油价格困境的解决必须建立与国际市场接轨的市场化定价机制。2008年12月以后,国家发改委按照“成本定价”的原则,开始参照国际市场上原油价格加权确定国内成品油价格,只要国际油价波动的上限不长时间高于 80美元/桶,国内成品油价格就紧跟国际原油价格的波动调整,而且油价调整趋于常态化,这就是所谓的“间接接轨”方式。显然,这种定价方式是一种向市场化过渡的机制,这样的定价模式将直接导致国际原油价格的波动对中国成品油价格的影响,因此通过对国际石油价格风险的刻画,研究中国成品油价格风险管理问题,以减轻国际油价波动对国内成品油市场的冲击就有着特别重要的意义。由于目前中国采用 Brent、Dubai、Minas3地原油市场价格加权确定成品油价格,笔者主要研究这 3个市场的原油价格风险和中国成品油定价的权重选择以及价格风险管理问题。

一、文献综述

国际油价波动始于 20世纪 70年代的第四次中东战争,之后,石油生产国和消费国对石油定价权的争夺日趋激烈,国际石油的定价体系逐渐形成了以期货定价为主的复杂体系,在这种方式下,石油价格的金融性逐步显现,油价波动成为常态。21世纪以来,国际油价从 2000年的 20美元/桶一度升至 2008年的 147美元/桶,受 2008年金融危机的影响又迅速跌至 40美元/桶以下,2009年 6月的油价回升至70美元/桶左右,之后半年维持在 80美元/桶附近。徐伟红等曾研究预测由于国际石油市场和石油工业的内在机制作用,高油价和油价波动状态将长期存在,这一点得到了印证[1]。

大部分学者将注意力集中在国际石油价格的波动和分布方面。Pindyck发现美国石油价格波动的半衰期为 5～10周[2]。与之对应,国内学者张跃军等对中国大庆原油价格建立了 GED-GARCH模型,认为中国国内石油价格波动也存在显著的 GARCH效应,但波动的半衰期仅为 5天,主要的原因是中国原油市场并非完全市场化运作[3]。冯春山[4]、潘慧峰和张金水[5]分别应用ARCH类模型研究了国际和国内的油价波动,前者使用 1986年 1月 -2002年 4月阿拉伯轻油月均价格数据发现了阿拉伯轻油市场的杠杆效应和波动聚集性,后者使用 1997年 1月 -2003年 11月中国国内原油价格 FOB周数据分析了国内油价波动的杠杆效应,并以不可再生资源理论的视角进行解释。魏巍贤使用马尔可夫机制转换模型刻画油价变化,认为油价变化有大幅上涨、小幅上涨和大幅下跌 3种形态,其中小幅上涨是最主要形态[6]。Ahn解释了石油价格分布的肥尾性的意义,认为在长期来看,肥尾分布能够稀释市场流动性[7]。Chang等则以多维ARCH类模型研究了WTI、Brent、Dubai和 Tapis原油现货及衍生品市场波动的相关关系[8-9],实证研究发现 GARCH效应在原油市场之间不是独立存在的,但连续条件相关关系并不存在,而在多元条件异方差模型中,VARMA-AGARCH模型比VARMA-GARCH模型和 CCC模型(conditionally constant correlation)能够更好地刻画原油市场的非对称效应和市场之间的溢出效应。

对于石油价格风险的管理问题,学术界也有许多论述。Mauro计算了炼油企业的市场风险 VaR (Value at Risk,风险价值),以此为基础对能源价格变化与能源企业市场风险间的关系进行分析[10]。Egenhofer等从国家角度探讨原油供应安全中减小风险管理成本的问题,并提出短期内平滑油价波动,长期内减少石油消费的建议[11]。黄运成等则探讨了石油衍生品市场对石油价格风险管理的作用,提出中国应当不断推进石油定价机制改革,建立交易所市场和场外交易市场 (OTC),并推动二者良性互动发展[12]。魏一鸣等全面分析了国际油价的上涨对中国经济社会的影响,并对石油管制政策和相关部门的技术进步进行了政策模拟,认为短期内坚持石油价格管制和技术进步能够缓解油价上涨对中国的影响[13]。潘慧峰和张金水以 Granger因果检验方法研究了国内外原油市场间的信息流动方向,发现中国大庆原油市场尚不能对WTI市场产生影响,中国对国际油价的波动仍处于被动接受状态,提出中国应当发展石油期货市场,建立规避国际油价波动的体系[14]。对于中国成品油定价以及价格风险管理问题,王小川提出完善市场准入制度、提高企业组织化程度、加强市场监测、建设石油商业储备等措施[15]。孙仁金在中国现行成品油定价机制的基础上,以“双向有效”为目标,提出完善市场准入和退出机制、严格按照国际市场调节国内成品油价等改进措施[16]。目前学术界在这一方面存在很大的不足,表现在对中国石油价格风险管理方面的定量研究还比较缺乏,对中国成品油市场的研究仅局限于定价机制的讨论,很少针对中国成品油用油成本进行价格风险管理系统量化研究。

笔者对 Brent、Dubai、Minas原油市场建立了GARCH模型,在扰动项条件正态分布的假设下实证研究了国际油价的波动风险,并检验了 GARCH模型下的VaR方法度量国际石油价格风险的有效性,在此基础上,考虑国际原油市场之间的相关关系,预测了成品油定价中最优的权重系数选择,并对结果进行了蒙特卡罗模拟验证。

二、理论模型

本部分主要阐述笔者所用的计量模型,这些模型中, VaR为油价波动风险的度量工具,扰动项正态分布的G ARCH模型为计算油价波动率的工具,检验 G ARCH模型有效性的方法为 Kupiec失败频率检验法[17]。

(一)VaR的概念及其蒙特卡罗模拟法

VaR是目前通行的风险度量工具,指某一金融资产或证券组合在一定的置信水平和未来特定的一段时间内的最大期望损失,可表示为:

其中,ΔP为投资组合在持有期Δt内的损失,c为置信水平,VaR为置信水平 c下处于风险中的价值。从统计的角度看,VaR是投资组合回报分布的一个百分位数。对于 VaR的计算有多种方法,比较常用的一种是蒙特卡罗模拟法。

蒙特卡罗模拟法是随着现代计算机技术的发展而发展成熟的一种计算风险价值 VaR的方法,主要用于变量的表达式不易得到的情形。其基本思路是首先根据其历史数据得到概率分布的参数,然后对生成金融变量的随机过程重复模拟,得到金融变量的整体分布情况,进而求得 VaR。在实证部分将使用这一技术计算石油市场组合的价格风险。

(二)GARCH模型

GARCH模型是处理具有非正态性、非独立性、肥尾性和波动集群性等条件异方差特征的数据的常用模型。已有研究表明,国际油价波动数据是典型的条件异方差数据,因此笔者采用 GARCH模型拟合,以便有效地消除数据中的条件异方差现象。结合我们对实证数据的分析,笔者选用 GARCH(1,1)模型,即:

式 (2)称为均值方程,xt是 1×(k+1)维外生变量向量,r是 (k+1)×1维系数向量;式 (3)称为条件方差方程,w是常数项,u2t-1是用均值方程的扰动项平方的滞后来度量从前期得到的波动性的信息,是指上期方差。据式 (3)所得油价的波动率可得油价的VaR估计值,即

其中σt|t-1为在 t-1期的信息下资产收益率的条件标准差,Pt-1为 t-1期的资产价格,如果仅仅考虑相对 VaR值,Pt-1可以省略。

(三)Kupiec的失败频率检验法

对VaR模型有效性的检验常用 Kupiec的失败频率检验法[17]。假定计算 VaR的置信度为 а,考察天数为 T,如果某交易日的收益率实际损失超过VaR模型所设定的估计值,就记模型失败一次,若失败次数为 N,则失败频率记为 p(N|T)。则令 p＊= 1-а,零假设为 p(N|T)=p＊,这样对模型准确性的评估就转化为检验失败频率 p是否显著不同于p＊。假定VaR估计具有时间独立性,失败出现次数可视为独立的贝努力试验,则 T次实验中失败 N次的概率为 (T/N)pN(1-p)T-N。Kupiec的零假设最适合的似然比率检验式为:

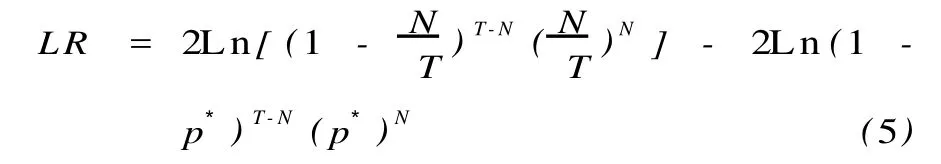
统计量 LR服从自由度为 1的卡方分布,此分布的 95%的置信区间临界值为3.84,99%的置信区间的临界值为 6.65,只要相应的置信区间上LR的值小于临界值,我们就接受模型。

三、实证分析

本部分的目的是在当前原油定价机制下寻求能够使中国成品油价格波动风险最小的策略。由于当前中国成品油定价机制中参照 Brent、Dubai和Minas3地原油市场,本部分主要确定能减小中国成品油价格风险的最优参照权重,采用的方法是通过扰动项正态分布假设下的 GARCH模型求解单一原油市场每期的波动率和 VaR值,通过概率积分转换求解原油市场间的线性相关系数,通过二次规划得到最优参照权重,而蒙特卡罗模拟技术将用于对这一权重值的验证。

(一)数据的选取与检验

笔者选取 Brent、Dubai和 Minas三地原油现货价格 1999年 9月至 2009年 8月的周收盘数据, Brent市场有 522个交易数据,Dubai和Minas市场有520个交易数据。Dubai和Minas市场缺少 1999年12月 17日和 2000年 9月 1日的数据,为了方便应用,笔者利用线性插值方法,假设这两个交易日的数据为其前一期和后一期数据的算术平均值,使 3个市场的数据长度相等。这些数据来源于美国能源情报署网站①http://tonto.eia.doe.gov/dnav/pet/pet_pri_wco_k_w.htm,数据处理使用 Eviews5.0软件。

以指数收益率计算每周的收益率,用 r表示:

对数据作条件异方差 (ARCH效应)检验、正态性检验等,结果如图 1至图 6所示。3组收益率数据均存在显著的ARCH效应,分布形态具有尖峰厚尾特征。

使用拉格朗日乘数法进一步检验数据中可能存在的ARCH效应如表 1所示,3组数据中均存在显著的ARCH效应。使用 ADF检验法对数据作平稳性检验,结果表明 3个数据序列都是十分平稳的。因此,笔者以 GARCH模型拟合。

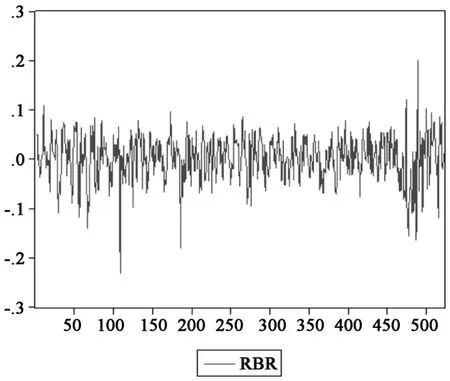
图 1 Brent市场日收益率波动图

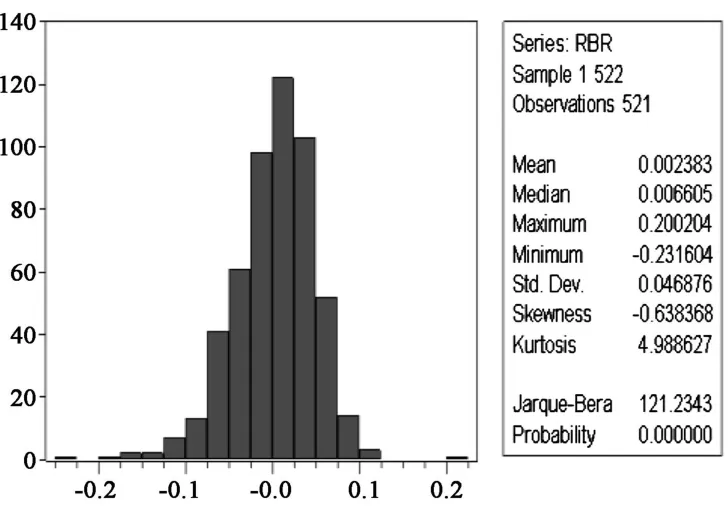
图 2 Brent市场日收益率正态检验图

图 3 Dubai市场日收益率波动图

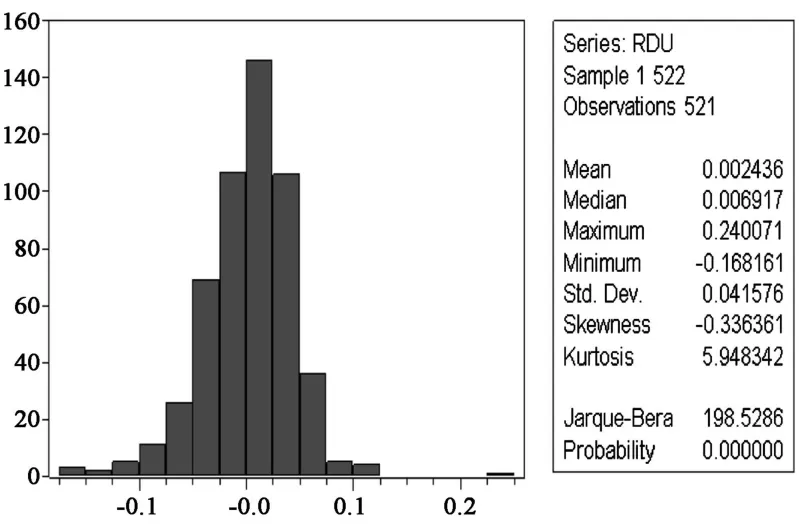
图 4 Dubai市场日收益率正态检验图

图 5 Minas市场日收益率波动图

图 6 Minas市场日收益率正态检验图

表 1 收益率序列的ARCH效应检验和平稳性检验结果

(二)GARCH模型对原油市场价格风险的刻画

使用基于扰动项正态分布的 GARCH模型处理数据,并计算 3个原油市场的 VaR值,即应用式(2)、(3)和 (4)可得表 2所示结果,经式 (5)检验, GARCH模型确定的波动率能够较准确地刻画原油市场的风险 VaR。这里,表 2中长期预测标准差是指由式(2)和 (3)估计的长期内原油市场收益率条件正态分布假设下的标准差。

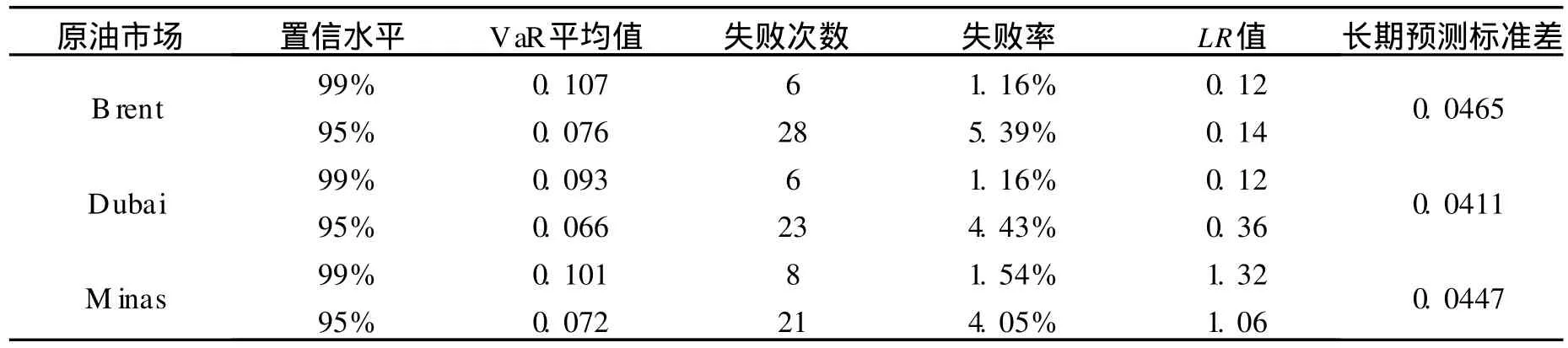
表2 GARCH模型对边缘分布的刻画

(三)成品油定价权重的选择

下面我们结合上述 3个市场原油价格的风险状况,分析中国成品油价格的确定问题,并给出一种成品油定价方法和模型。

1.原油市场的相关性

我们知道,国际原油价格波动的直接原因是受复杂因素扰动,比如运输条件的变化、天气和季节、政治事件和战争、美元汇率及金融市场的波动等等,都能对国际油价形成冲击。众多扰动因素中有的只对某一个市场存在影响,有的对多个市场存在影响,造成国际原油市场之间的相关性存在。笔者下面采用相关系数刻画 3个原油市场之间的相关性。

在 GARCH模型的条件正态分布假设下,对 3个原油市场收益率历史数据作概率积分变换,使用K-S检验法检验其是否服从均匀分布,结果如表 3所示,没有充分的理由拒绝概率积分变换后的序列服从[0,1]均匀分布,对变换后的序列做DW统计量自相关检验,序列也不存在显著的自相关性。因此,可以使用 GARCH所设定的原油市场分布和概率积分变换方法进行成品油价格风险的模拟。

计算概率积分变换后的序列间的线性相关系数(ρ),结果见表 3。这表明通过合理的组合可以降低3个市场组合收益的风险,进而实现成品油价格风险管理目标。

表 3 原油市场的相关系数和 K-S检验

2.最优权重的理论值确定

由于 GARCH模型是一个典型的时变系统,笔者讨论以 GARCH模型预测的未来原油市场长期波动情形下的权重选择。中国成品油定价方式以 Brent、Dubai、Minas3地市场原油的加权价格为基础加固定的基准点,令 3个市场对应权重分别为α,β,γ。为方便起见,设基准点为常数A。

在一段时期内,令 Brent、Dubai、Minas市场原油的价格向量为 (p1,p2,p3),收益率向量为 (r1,r2,r3),则成品油的价格可以用 Brent、Dubai、Minas市场的价格表示:

在式 (11)式中,CPY是以指数收益率表示的成品油价格变动指标,成品油价格风险管理的目的就是使CPY的波动最小,即选择α,β,γ的估计值 ^α,^β, ^γ使 CPY的估计值 C^PY的波动最小。

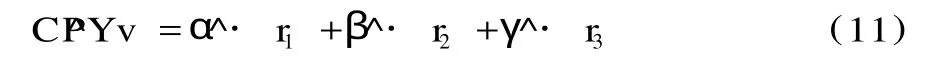
根据前文所述,可以设定原油市场分布为均值为 0,标准差为长期预测值的正态分布,则上述问题变为对α,β,γ求解二次规划,如下:

在式 (13)中,σCPY为成品油价格变动指标的波动率,σ1,σ2,σ3分别表示 Brent、Dubai和Minas市场的长期预测波动率,ρ12,ρ23,ρ13分别表示 Brent与Dubai、Dubai与Minas以及 Brent与Minas市场间的相关系数。求解上述二次规划得最优权重及相应的成品油价格波动的最小值:

显然,与表2中 G ARCH模型刻画的单个原油市场的长期预测波动率相比,在最优权重的理论值下,成品油价格的波动率低于任何一个原油市场的波动率。

(四)理论权重与经验权重的比较

以理论的最优权重作为价格风险管理策略,笔者在预定的经验权重α、β、γ下,利用蒙特卡罗模拟技术,计算CPY的VaR以检验价格风险管理策略的有效性。

表 4 理论权重与经验权重下的成品油价格风险比较

对比情形(Ⅰ)和情形 (Ⅱ),我们发现 4个 VaR值指标情形 (Ⅰ)均优于情形 (Ⅱ),所以使用情形(Ⅰ)的权重对成品油定价能够降低风险。

假设当期用油成本为 75美元/桶,在 95%的置信水平下,根据式 (6),如果国际市场原油价格下跌,情形 (Ⅰ)确定的下期油价为 72.10美元 /桶,情形(Ⅱ)确定的油价为 71.94美元 /桶;如果国际市场原油价格上涨,情形 (Ⅰ)确定的下期油价为 78.90美元/桶,情形 (Ⅱ)确定的油价为 79.07美元 /桶。这就是说,在国际原油市场波动率不变的情况下,用情形(Ⅰ)所确定的权重定价能够减少用油成本波动0.16～0.17美元 /桶。

四、结论及建议

笔者以扰动项为正态分布的 GARCH模型研究了Brent、Dubai和Minas原油市场的价格波动风险,以 Kupiec的失败频率检验法检验模型的有效性,结果表明,模型能够刻画考察期的原油收益率波动特征,也能够较好地度量 3地原油市场的价格风险。由于 3地原油市场油价与中国成品油的定价密切相关,笔者对 3个原油市场的历史数据拟合结果进行相关性分析,计算了原油市场之间的相关系数,通过组合波动最小原理得出在成品油定价过程中参照 3地市场的权重比为 0.238 9∶0.575 9∶0.185 2时,中国成品油用油成本的波动达到最小值,进而,笔者通过蒙特卡罗模拟验证了在这一结果,在 75美元/桶的国际油价水平下,置信水平取 95%,使用最优权重能够减少用油成本波动 0.16～0.17美元/桶。这一结果能够方便地用于中国原油贸易以及成品油价格风险管理。

国际油价的波动给中国经济运行带来了巨大的风险,中国成品油定价采用原油成本法的目的是逐步实现国内石油消费与国际市场接轨,这必然要求中国利用国际原油市场的风险管理方法加强自身成品油价格风险管理。中国石油部门应当适应新的经济形势,以定性和定量相结合的办法研究国际油价及其波动风险,对相关的国际原油市场建立风险模型,在国际石油市场价格风险与国内油品价格风险之间的关系充分量化研究的基础上,形成完善的价格风险管理的体系,保障中国石油价格安全。

[1]徐伟红,来君,孙大利.对国际石油市场的理论分析和展望[J].重庆大学学报 (社会科学版),2006,12(6):19-23.

[2]P INDYCK R S.Volatility in natural gas and oil markets [J].The Journal of Energy and Development,2004,30 (1):1-20.

[3]张跃军,范英,魏一鸣.基于 GED-GARCH模型的中国原油价格波动特征分析[J].数理统计与管理,2007,26 (3):398-406.

[4]冯春山,吴家春,蒋馥.国际石油市场的 ARCH效应分析

[J].石油大学学报 (社会科学版).2003,19(2):18-20. [5]潘慧峰,张金水.基于 ARCH类模型的国内油价波动分

析[J].统计研究,2005(4):16-20.

[6]魏巍贤,陈智文,王建军.三状态马尔可夫机制转换模型研究——在世界油价波动分析中的应用[J].财经研究, 2006(6):120-131.

[7]AHN D P.Fat tails and futures markets illiquidity:Theory and evidence from crude oil and natural gas[EB/OL]. (2007-11-10).http://www.ssrn.com.

[8]CHANGChia-lin,McALEERM,TANSUCHAT R.Modelling Conditional Correlations for Risk Diversification in Crude OilMarkets[EB/OL]. (2009-05-20).http:// www.ssrn.com.

[9]CHANG Chia-lin,McALEER M,TANSUCHAT R.Forecasting volatility and spillovers in crude oil spot,forward and futuresmarkets[EB/OL].(2009-05-16).http:// www.ssrn.com.

[10]MAURO A.Price Risk Management in the energy industry:The value at risk approach[EB/OL].(1999-06-22).http://www.ssrn.com.

[11]EGENHOFER C,G IALOGLOU K,LUC IAN I G.Marketbased options for security of energy supply[EB/OL]. (2004-09-26).http://www.ssrn.com.

[12]黄运成,李畅,马卫锋 .中国石油价格风险管理的困境与选择[J].世界经济研究,2005(10):22-26.

[13]魏一鸣,焦建玲,梁强,等.油价长期高位对我国社会经济的影响与对策 [J].中国科学院院刊,2008,23(1): 11-15.

[14]潘慧峰,张金水.国内外石油市场的信息流动与一体化[J].重庆大学学报 (社会科学版),2008,14(2):20-26.

[15]王小川.我国成品油市场管理的改革和发展[J].国际石油经济,2008(4):22-25.

[16]孙仁金,马杰,王琳旋.“双向有效”的成品油定价机制调整方法研究 [J].价格理论与实践,2009(7):39-40.

[17]KUPIEC P.Techniques for verifying the accuracy of risk managementmodels[J].Journal ofDerivatives,1995(3): 73-84.

[18]DORAN J S,RONN E.Computing the Market Price of Volatility Risk the Energy CommodityMarkets[EB/OL]. (2008-01-06).http://www.ssrn.com.

[19]P IL IPOV IC D.Energy risk[M].New York:TheMcGraw-Hill Companies,Inc,2007:35-254,375-454.

[20]DORAN J S.The influence of tracking error on volatility risk premium estimation[EB/OL]. (2006-05-21). http://www.ssrn.com.

[21]高铁梅.计量经济分析方法与建模[M].北京:清华大学出版社,2006.

Research on InternationalO il Price Volatility and China’s Refined O il Price Risk

SHEN Pei-longa,b,XING Tong-zhenga
(a.School of Finance and B anking; b.Applied Econom ic Research Institute,Shanxi University of Finance and Econom ics,Taiyuan 030006,P.R.China)

The price risk ofBrent,Dubai andMinasCrudeOilmarketwith GARCH model atNormal distribution is analyzed in thispaper,and the results are examined by using Kupiec test.The price volatility is significantly described;price risks are measured aswell.Because China sets its refined oil price according to Brent,Dubai and Minas Crude oilmarket,the correlation between the three markets are analyzed based on their historical data.The results present that theweightsover the threemarkets at0.2389:0.5759:0.1852 would bemin imized oil cost volatility in China’s refined oilmarket.The results are tested byMonte Carlo simulation,too.Giving the international oil price at 75 dollars/barrel and taking 95%confidence level,China’s oil cost volatility could be reduced 0.16-0.17 dollars/barrel in the method mentioned in this paper compared with common empiricalmethods.

refined oil;international oil price;GARCH model;price risk

F764.1

A

1008-5831(2011)01-0035-07

(责任编辑 傅旭东)

2009-11-14

国家自然科学基金项目(70873078)

沈沛龙(1964-),男,山西省襄汾县人,山西财经大学应用经济研究院院长,山西财经大学财政金融学院教授,博士,博士研究生导师,主要从事金融工程与风险管理研究。