畜产品价格定量预测方法评析*
唐江桥
(福建农林大学经济与管理学院,福建福州350002)
畜产品价格定量预测方法评析*
唐江桥
(福建农林大学经济与管理学院,福建福州350002)
通过文献研究,本文归纳出定量预测畜产品价格的方法模型主要有回归模型、Box-Jenkins方法和VAR模型以及神经网络模型。没有明确的证据显示某一种方法或模型一定优于另一种方法或模型。在畜产品价格预测中,如果需要得到较为精确的预测结果,可供借鉴的做法是采用两种以上的方法或模型进行比较,或者进行组合。
畜牧业;畜产品;价格预测;Box-Jenkins方法;VAR模型;神经网络模型
畜牧业在农业中的地位随着我国经济的发展越来越重要。根据《中国统计年鉴2009》中的相关数据可知,2008年我国畜牧业占农业总产值的比重达到35.5%,而1980年只占农业总产值的18.4%,畜牧业已经从改革初期的家庭副业上升为现代农业的支柱产业。随着畜牧业比重的上升,畜产品价格的变动对国民经济的影响越来越大。2005年以来全国范围内生猪价格的剧烈波动,对生猪生产者和猪肉消费者都产生了巨大的冲击,也严重影响到了农民的收入;而2007年猪肉价格的暴涨更是直接拉动了我国CPI指数的快速上扬。除生猪价格波动造成了重大影响外,价格波动导致奶业波动、蛋鸡波动等都影响了人民的正常食品消费。因此,畜产品价格的频繁、大幅变动已经对人们的食物消费结构造成了严重影响,甚至还造成了国民经济的不稳定,影响到我国经济的持续快速健康发展。畜产品价格从高点的快速下跌更使得大量的畜禽养殖户,尤其是散养户处于亏损状态,甚至破产。以上现实表明,对我国的畜产品价格进行预测研究很有必要。本文对已有文献中对畜产品价格预测所用的方法进行归纳和评价,以便进一步探索我国畜产品价格的预测方法,提高我国的畜产品价格预测精度。
一、定量预测方法和模型
相比预测理论发展的滞后,当前在进行一项经济预测时可供选择的方法和模型非常多。经济预测作为经济研究的主要领域之一,其方法的应用非常广泛,可以说各行各业的供给、需求和价格预测都使用到了现代经济预测方法。现代经济预测方法包括定性方法和定量方法两大类。定性方法用来判断价格的走势,定量方法则给出明确的预测值。本文的研究范围是定量方法在畜产品价格预测中的应用。应用于畜产品价格预测中的定量方法和模型大致可分为三类。
(一)回归模型预测法
回归模型预测法需要清楚被解释变量受到哪些解释变量的影响,在此基础上根据经济学理论建立模型。回归模型预测的优点很明显:可以清楚地看到被解释变量的变动是由哪些解释变量的变动所导致的。但是,回归模型需要把一些变量看成是内生的,另一些变量看成是外生的,具有一定的主观性。另外,由于经济系统的复杂性,要确定一个被解释变量有多少影响它的解释变量以及这些解释变量分别是哪些,是一件非常不容易的事情。
回归模型最简单的是线性模型。经典双变量线性回归模型的一般形式为:

其中yt为被解释变量,xt为解释变量,β0和β1为待估参数,εt为服从独立同分布的随机误差项。
运用上述回归模型进行向前一步预测时,首先需要确定解释变量xt+1的值,代入上式后就可以对被解释变量yt+1进行预测。将上式中的单变量换成向量形式,就是多方程回归模型。
线性回归模型是运用较早的预测模型之一,模型的具体形式需要根据所研究问题的不同而变化,如DO CANTO(1972)[1]在预测美国肥猪价格时所采用的基本模型形式为:
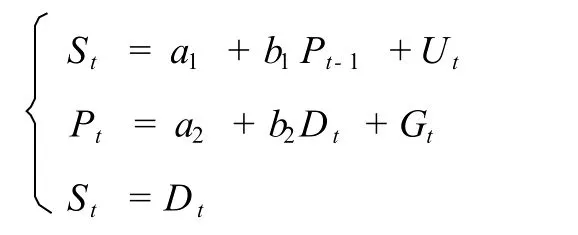
其中,St为本期供给,a和b为待估参数,Pt-1为上期价格,Pt为本期价格,Ut和Gt为误差项。可以看出,上述方程组实际为蛛网模型的函数形式。
对于回归模型来说,确定解释变量不是一件容易的事情。解释变量太少,难免遗漏有影响的重要变量;解释变量太多,模型将变得复杂,样本数据的获取难度也会增加。如果是联立方程组,则在估计前需要保证可识别性,而且常常需要假定某些变量仅出现在某些方程中,难以保证其客观性。应用回归模型进行畜产品价格预测的文献更多的集中于20世纪70年代,如ROY(1971)、LEE(1971)、FOOTE et al.(1976)等[2-4]。
(二)Box-Jenkins方法和VAR模型
自从Box和Jenkins的著作发表以来,用于单变量时间序列预测的ARMA(Auto-Regressive Moving-Average)模型得到了迅速而广泛的应用。ARMA模型实际上是MA模型和AR模型的综合,模型的核心理论为沃尔表示定理(Wold’s representation theorem)。沃尔表示定理的含义为:任意协方差平稳序列的模型都可以表示成白噪声的无限阶分布滞后[5]。ARMA(p,q)模型的一般化形式如下:

其中εt服从均值为0、方差为σ2的白噪声分布,φ1…φp和θ1…θq为待估参数。ARMA模型要求所分析的时间序列是平稳的,但是原始的时序数据中往往包含有趋势性和季节性成分导致序列是非平稳的,所以我们常常需要运用差分的方法来消除原始序列中的趋势性和季节性。差分后的ARMA模 型 称 为AR IMA(Auto-Regressive IntegratedMoving-Average)模型。进行d阶差分后的ARMA(p,q)模型记为AR IMA(p,d,q)模型。
在对畜产品价格的预测中,有一些文献运用了AR IMA模型。如Oliveira等(1979)[6]运用AR IMA模型拟合来自不同市场的6种类型活牛现货价格序列和芝加哥期货市场的活牛价格序列,拟合样本区间为1972年1月到1976年12月的周价格,预测区间为1977年1月到1977年8月的周价格。研究结果发现,对于现货价格序列来说,AR IMA模型的短期预测更加精确;对于期货价格序列则是长期预测更为精确。使用AR IMA模型进行畜产品价格预测的研究还有BOURKE(1979)、 INGCO(1983)和KARBASI等(2009)[7-9]。国内也有文献运用Box-Jenkins方法进行畜产品价格预测,如姚霞等(2007)、傅如南等(2008)和刘峰等(2009)[10-12]。
Box-Jenkins方法研究的对象是单变量时间序列,对于多变量时间序列系统的研究多运用VAR (VectorAuto-Regression)模型。VAR模型实际上是VARMA模型的简化,但是后者因参数过多带来很多问题而少有应用。VAR(p)模型的一般形式为:

其中,yt是m维内生变量向量;xt是d维外生变量向量;A1…Ap和B1…Br是待估参数,内生变量和外生变量分别有p和r阶滞后期;εt是随机扰动项,同期之间可以相关,但不能有自相关,不能与模型右边的变量相关。
VAR模型在畜产品价格预测研究中应用颇多。如GOODW IN(1992)[13]使用变参数VAR模型和逐步跳跃的VAR模型对美国牛的季度价格(样本区间为1970—1990年)进行估计,发现在样本区间有明显的证据表明存在结构性变动。还有THRAEN等(2002)和ZAPATA、GARC IA (1990)[14-15]运用BVAR(Bayesian VAR)模型分别对美国的牛奶价格和牛的价格进行了预测。国内有马孝斌等(2007)[16]用VAR模型对北京市2000年1月至2006年6月的生猪月度价格进行了拟合,并对2006年7至12月的价格进行了预测。
Box-Jenkins方法虽然可以很好地拟合单变量时间序列数据,并且能得到效果不错的短期预测值,但这种方法不是建立在经济理论的基础之上,它实际上是一种复杂的滤波技术而不是经济模型[17],所以当我们用这种方法得不到理想的预测结果时,将找不到原因何在。此外,如果我们的目的是为了解释经济系统的行为而不仅仅是得到一个预测结果,那么就不能使用Box-Jenkins方法,因为这种方法没有经济理论基础,不能用来检验复杂的经济现象的假设。
与单变量模型相比,VAR模型考虑了变量之间的交互变化。前述第一类回归模型需要事先区分变量是内生还是外生的,而VAR模型不需要进行这样的区分,这在一定程度保证了模型设定的客观性。VAR模型的倡导者强调此方法简单而且估计也简单,但VAR模型的批评者也指出如下问题:VAR利用较少先验信息,所以缺乏理论基础;VAR的重点在预测,不适于做政策分析;VAR模型的滞后长度难以确定;在一个有m个变量的VAR模型中,所有的m个变量都应该是平稳的; VAR往往需要估计脉冲响应函数(impulse response function)。
(三)神经网络模型
神经网络模型的应用非常广泛,在畜产品价格的预测中也有一些文献进行了应用研究。在神经网络模型中,应用最多的是BP(Back Propagation)人工神经网络模型,模型的基本结构图如图1所示。BP神经网络有三层前馈网络:输入层、隐含层和输出层。其中的隐含层可以只包含一层网络,也可以包含多层网络,因此BP网络是一种多层前馈神经网络。BP神经网络神经元的传递函数是S型函数,输出量为0到1之间的连续量,它可以实现从输入到输出的任意非线性映射。经输入层输入数据样本后,模型按期望输出与实际输出误差平方和最小化的原则进行学习过程,通过权值矩阵和阈值向量的不断调整,可以实现误差平方和达到所要求的范围之内。
KARBASI等(2009)[9]对伊朗禽肉价格进行预测时应用了静态和动态神经网络模型,并将预测结果和线性预测模型的结果进行了比较,所得的结论是动态神经网络模型的预测结果最理想,其次是静态神经网络模型,线性模型的预测结果在三者中最差。马雄威和朱再清(2008)[18]将BP神经网络模型和灰色系统进行组合,使用我国2006年4月至2007年11月的猪肉月度价格作为样本,预测了我国2007年12月至2008年9月的猪肉价格。预测结果认为我国的猪肉价格在2007年12月至2008年9月期间虽然呈上涨趋势,但波动幅度不会很大。

图1 BP人工神经网络模型
当然,预测模型和方法非常多,除了上述模型外,还有其他模型可以应用到畜产品价格的预测研究中来,如GARCH模型。RAM IREZ和FAD IGA(2003)[19]就曾运用此模型来预测大豆、高粱和小麦价格。预测技术的发展为我们提供了更多的预测方法和模型,一个自然的问题就是:在应用研究中我们如何选择合适的预测方法?
二、不同预测方法的比较
面临同样的预测研究对象时,可以有多种不同的方法和模型可供选择,究竟选择哪一种方法和模型是合适的?有没有一种选择标准提供给我们作为指导或参考呢?迪博尔德(2003)[5]将预测方法和模型的选择原则概括为KISS原则:“简约但不简单”(Keep It Sophisticatedly Simple)。所谓简约原则。在其他条件相同的情况下,简单优于复杂。之所以认为简单模型优于复杂模型,是基于如下一些理由:(1)简单模型的参数易于精确估计;(2)简单模型易于解释、理解和检查;(3)简单模型易于把握其内在机制,有利于决策;(4)简单模型减小了数据挖掘的范围,因为数据挖掘往往会导致模型和数据的过度拟合。现代的经济预测专家普遍认同模型选择的简约原则。在畜产品价格预测的研究文献中,也有不少专家学者对不同的经济预测方法进行了比较研究。
HELMERS和HELD(1977)[20]使用了不同的方法对美国内布拉斯加州奥马哈地区的肉牛和肉猪价格进行了预测,比较了各种预测结果的精度。他将所使用到的预测方法分为三大类:第一类为简单模型(simple models),包含了5个子模型(用上年同期的价格作为预测价格,用现期价格作为四个月后的预测价格,随机抽取去年某一周的价格作为预测价格,用去年的平均价格作为预测价格,用过去8个月的价格趋势预测4个月后的价格)。第二类模型利用芝加哥期货市场的相应期货价格作为预测价格。第三类利用经验信息进行预测,包括两个子模型,一是利用过去成功的农场主的预测作为预测值,二是利用USDA的预测价格。文章对不同预测方法取得的结果与实际值进行了比较,分析了实际值和预测值之间的平均误差和标准差,得到的结论为:不能简单地认为所用的某一种方法比另一种方法更精确,即使是那些“单凭经验的方法”(rule of thumb),如成功农场主的预测,也有其可取之处。
BOURKE(1979)[7]比较了Box-Jenkins方法和线性回归方法在预测美国牛肉价格的表现。他的线性回归模型包含的自变量非常多,有牛肉消费量、羊肉消费量、猪肉消费量、烤肉消费量、火鸡肉消费量、上一期的可支配收入、失业率、时间变量、季节(或月度)虚变量。用来比较的统计量有根均方误(RootMean Squared Error,RMSE)和希尔不等系数(Theil’s Inequality Coefficient),还有一个对转折点(Turning Points)判断能力的比较。Bourke认为如果在序列中存在转折点,那它就会改变预测的方向或者是实际序列的变动方向。研究结果表明,Box-Jenkins方法不论是在预测精度方面,还是在转折点判断方面都要优于所用的线性回归模型。而且他在用线性回归模型进行预测时,自变量的取值是实际值,但我们在真正做预测时,必须首先对自变量的值进行预测,然后才可能得到因变量的回归预测结果,这意味着因变量的预测误差将会更大。
KARBASI等(2009)[9]对当前较为流行的动态非线性模型、静态非线性模型和线性模型的预测表现进行了比较研究。他用含输入的神经网络自回归模型(NeuralNetworkAuto-Regressivemodel with exogenous inputs,NNARX)代表动态非线性模型,用人工神经网络模型(ArtificialNeuralNetwork model,ANN)代表静态非线性模型,用AR IMA模型代表线性模型,分别用这三个模型拟合伊朗2002年3月到2006年3月的禽肉市场价格周序列做向前一周、两周和四周的预测,并用2006年4月到2007年12的价格进行预测结果检验。所用的比较统计量为判定系数R2、平均绝对误差MAD、均方误(MSE)和根均方误(RMSE)。结果发现,NNARX和ANN模型的预测结果要优于AR IMA模型,而NNARX模型要优于ANN模型。他的研究结果似乎支持这样一种观点,即复杂模型的预测结果要好于简单模型。
随着预测技术的不断发展,对畜产品价格进行预测时可供选用的方法和模型也愈加丰富,同时也会有更多的研究比较不同方法和模型的预测效果。就现有的研究成果来看,并没有确凿的证据显示某一种方法一定优于另一种方法。在具体应用中,我们可以根据自己的需要来选择不同的预测方法和模型。更复杂的模型所需要的成本更高,如果需要的预测结果并非那么精确,则可以选择相对简单的方法和模型。倘若预测失误会导致重大的损失,则可以同时选用多种方法并进行比较,以便使最终的决策得到更多的支持。
三、总结和评论
通过对现有文献的梳理和归纳,发现对畜产品价格进行定量预测的主要方法可以分为三类:回归模型预测法、Box-Jenkins方法和VAR模型、神经网络模型。当然,定量预测方法和模型有许多,并且正处于快速发展之中,具体用什么方法对畜产品价格进行定量预测更合适,需要结合具体情况来定,而非只有以上三种方法可用,本文只不过是在文献研究中发现使用这三种方法的研究者比较多而已。
当应用不同的方法和模型对畜产品价格进行预测时,并没有一个统一的标准说某一种方法一定优于其他方法,因此在研究中采用哪一种方法,依然强调需要根据所研究的具体对象来进行确定。有时两种以上预测方法的组合,即组合预测也是可供选择的方法之一。
本文研究的是定量预测方法在畜产品价格研究中的应用,而在实际预测中,作出定性判断是必要的。不论采用什么方法,定量预测结果必须和定性判断的结果相一致,否则需要查找原因,重新进行预测。具体对畜产品价格而言,因为畜产品的需求价格弹性和收入弹性都比较低,同时畜产品的生产又需要一定的周期(牲畜的自然生长过程),这可能导致畜产品价格的波动幅度具有不断扩大的趋势。我国正处于经济转型期,许多与市场经济相配套的制度建设尚待建立和完善,当前出现的价格波动有可能是市场本身造成的,也有可能是市场不完善所导致的。市场造成的畜产品价格波动可以通过定量预测方法寻找规律,得到较好的预测结果;而市场不完善导致的价格波动,则需要更多的定性判断来进行预测。
[1]DO CANTO W L.A Recursive Model for Forecasting Quarterly and Monthly U.S.Hog Prices[D].Michigan State University,Depar tment of AgriculturalEconomics,1972.
[2]ROY S K.Prediction of Shell Egg Price—A Shortrun Model[J].Southern Journal ofAgricultural Economics, 1971,3(1):175-179.
[3]LEE MK.An October Prediction ofthe Detroit November Price for Eggs at the Wholesale Level[D]. Department of Agricultural Economics,Michigan State University,1971.
[4]FOOTE RJ,ROY S K,SADLERG.Quarterly Prediction Models for Live Hog Prices[J].Southern Journal of Agricultural Economics,1976,8(1): 127-129.
[5]D IEBOLD F X.经济预测[M].张涛,译.北京:中信出版社,2003:40,119-120.
[6]OL IVEIRA R A,O’CONNOR C W,S M ITH G W. Short-Run Forecasting Models of Beef Prices[J]. Western Journal of Agricultural Economics,1979,4 (1):45-56.
[7]BOURKEIJ.ComparingtheBox-Jenkinsand Econometric Techniques for ForecastingBeef Prices[J]. Review ofMarketing and Agricultural Economics,1979, 47(2):95-106.
[8] INGCO M D.Economitric and AR IMA Models in Predicting Cattle and Hog Prices:An Evaluation[D]. Michigan State University,Department of Agricultural, Food,and Resource Economics,1983.
[9]KARBASIA,LASKUKALAYEH S S,FAH IM IFARD S M.ComparisonofNNARX,ANNandAR IMA Techniques to Poultry Retail Price Forecasting[J]. International Association of Agricultural Economists, 2009(Conference):16-22.
[10]姚霞,彭汉艮,朱艳,曹卫星,张卫建.时鲜农产品价格预测的AR IMA时序模型构建与应用[J].农业系统科学与综合研究,2007(1):89-94.
[11]傅如南,林丕源,严尚维,孙爱东.基于AR IMA的肉鸡价格预测建模与应用[J].中国畜牧杂志,2008 (20):17-21.
[12]刘峰,王儒敬,李传席.AR IMA模型在农产品价格预测中的应用[J].计算机工程与应用,2009(25): 238-240.
[13]GOODW IN BK.Forecasting Cattle Prices inthe Presence of Structural Change[J].Southern Journal of Agricultural Economics,1992,24(2):11-22.
[14]THRAEN C S,THOMPSONS R,GOHOUT W. Conditional Forecasting for the U.S.Dairy Price Complexwith a Bayesian Vector Autoregressive Model [J].American Agricultural Economics Association, Annualmeeting,July 28-31,2002,LongBeach,CA.
[15]ZAPATA H O,GARC IA P.Price Forecasting with T ime-Series Methodsand Nonstationary Data:an Application to Monthly U.S.Cattle Prices[J]. Western Journal of Agricultural Economics,1990,15 (1):123-132.
[16]马孝斌,王婷,董霞,王楚端.向量自回归法在生猪价格预测中的应用[J].中国畜牧杂志,2007(23): 4-6.
[17]NAYLOR T H,SEAKS T G,W ICHERN D W.Box-JenkinsMethods:anAlternative to EconometricModels [J].InternationalStatisticalReview/Revue Internationale de Statistique,1972,40(2):123-137.
[18]马雄威,朱再清.灰色神经网络模型在猪肉价格预测中的应用[J].内蒙古农业大学学报,2008(4): 91-93.
[19]RAM IREZ O A,FAD IGA M.Forecasting Agricultural CommodityPrices withAsymmetric-ErrorGARCH Models[J].Journal of Agricultural and Resource Economics,2003,28(1):71-85.
[20]HELMERS,G A,HELD,LJ.Comparisonof Livestock Price Forecasting Using S imple Techniques, For ward Pricing and Outlook Infor mation[J].Western Journal of Agricultural Economics,1977,1(1): 157-160.
(责任编校:夏东,朱德东)
L iterature Review on Application of QuantitativeM ethods to Prediction of An imal Products Price
TANG Jiang-qiao
(College of Econom ics and M anagement,Fujian Agriculture and Forestry University,Fujian Fuzhou350002,China)
Through literature research,this paper summarized main quantitative prediction models of animal products price including regression model,Box-Jenkins method,VAR model,and the neural network model.There is no obvious conclusive evidence that a method or a model is better than anothermethod or model.If more accurate prediction results are needed about prediction of animal products price,the feasible method is to compare or combine two methods ormodels ormore.
animal husbandry;an imal products;price prediction;Box-Jenkinsmethod;VAR model;neural network model
F316.3;F224.0
A
1672-0598(2011)01-0048-06
12.3969/j.issn.1672-0598.2011.01.008
2010-10-28
福建省科技厅软科学项目(2009R0007)“软科学的方法选择与应用”
唐江桥(1980—),男;博士研究生,在福建农业大学经济与管理学院学习,主要从事农业经济理论与政策研究。

