模糊层次分析法在盾构机型优选中的应用
蔡亮学,何利民,吕宇玲,张德桥,陈雪华
(1.中国石油大学油气储运与建筑工程学院,山东青岛 266555;2.中国石化集团管道储运公司,江苏徐州 221000)
模糊层次分析法在盾构机型优选中的应用
蔡亮学1,何利民1,吕宇玲1,张德桥2,陈雪华2
(1.中国石油大学油气储运与建筑工程学院,山东青岛 266555;2.中国石化集团管道储运公司,江苏徐州 221000)
盾构穿越工程中,选用合适的盾构机型以适应复杂多变的地质条件与施工要求至关重要,但目前多依靠施工经验定性判断。引入定性评价与定量分析相结合的模糊层次分析法(FAHP),通过建立递阶层次模型、确定模糊一致矩阵、计算指标权重 3个步骤进行盾构机型的优选。该方法在宜昌长江盾构穿越中的成功应用表明,建立递阶层次模型是 FAHP的关键环节;指标权重仅具有相对意义,用于对比排序,其数值没有实际的物理意义。
模糊层次分析法;盾构;优选;矩阵;权重
0 引言
与传统隧道开挖方式相比,盾构法在掘进速度、工程质量、环境保护以及安全性等方面具有独到的优势,在地下空间的工程建设中得到越来越广泛的应用。为适应复杂多变的地质条件与施工要求,大量新型盾构技术应运而生,如扩径盾构施工法、球体盾构施工法、H&V盾构施工法、变形断面盾构施工法等等,各方法均有特定的盾构机型配合使用。按结构特点与开挖方法,盾构机型可分为 2大类:闭胸式与敞胸式,进一步可细分为 6种机型[1],如图 1所示。面对多样的盾构机型,针对特定工程条件选用最优机型成为建设中的首要问题,当前多依靠施工经验定性判断[2~4],其准确性与普适性均受到较大限制。为此,引入在工程决策中应用日益广泛的模糊层次分析法 (FAHP)[5,6]进行盾构机型优选,建立一种科学合理的定量评价方法,并以“川气东送”管道宜昌长江盾构穿越工程为例,详细给出 FAHP优选盾构机型的分析步骤。
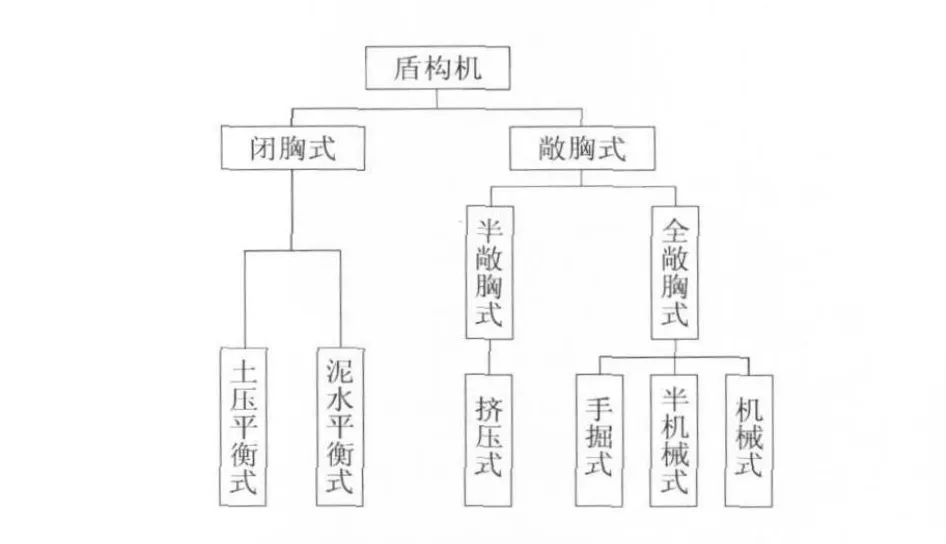
图1 盾构机型的分类
1 模糊层次分析法
1.1 FAHP概述
20世纪 70年代,为解决“根据各工业部门对国家福利贡献大小进行电力分配”课题,美国运筹学家 Saaty应用网络系统理论与多目标综合评价方法提出了定性分析与定量分析相结合的层次分析法(AHP),通过明确问题、建立层次分析结构模型、构造判断矩阵、层次单排序、层次总排序 5个步骤求解各层次构成要素对总目标的组合权重,进而计算不同可行方案的综合评价值,为评选最优方案提供依据。AHP法的概念清晰易懂,在现代管理决策领域得到大量应用。然而,AHP也有自身难以克服的不足:(1)检验、调整判断矩阵是否具有一致性难度大;(2)检验判断矩阵一致性的标准 CR<0.1缺乏科学依据;(3)判断矩阵的一致性与人类思维的一致性有显著差异。为解决上述问题,模糊层次分析法(FAHP)应运而生,通过引入模糊一致矩阵有效解决了判断矩阵一致性的相关缺陷,近年来在各种决策领域得到越来越广泛的应用。
1.2 FAHP的主要分析步骤
1.2.1 建立递阶层次结构模型
针对特定的实际问题,深入分析各影响因素及其相互之间的联系,按照不同属性将其自上而下分解成若干层次,同一层的因素从属于上一层的因素或对上层因素有影响,且同时支配下一层的因素或受到下层因素的作用。通常情况下层次结构模型自上而下可分为 3个层次:目标层、准则层与方案层。一般目标层只有 1个因素,准则层与方案层包含多项因素,当准则层的因素过多时可进一步分解出子准则层。
1.2.2 确定优先关系矩阵
优先关系矩阵 F表示针对上一层某因素,本层次与之有关因素之间相对重要性的比较。将由等待进行重要性比较的因素构成的指标集记为 F0={f1, f2,…,fn},所针对上层某因素 A的优先关系矩阵 F =(fij)n×n:
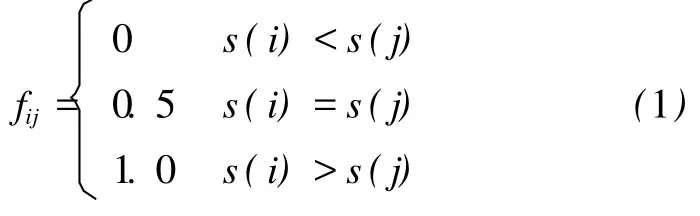
式中:s(i)、s(j)——分别表示指标 fi与 fj的相对重要性程度。
1.2.3 将优先关系矩阵改造为模糊一致矩阵
优先关系矩阵 F为模糊互补矩阵,为保证与人类决策思维的一致性相协调,需将其改造为模糊一致矩阵,按照文献[7]的定义,若矩阵 R=(rij)n×n满足:rij=rik-rjk+0.5,则为模糊一致矩阵。可按下述步骤改造矩阵:
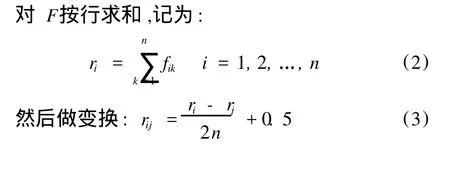
据此建立的判断矩阵可保证模糊一致性,证明详见文献[8]。
1.2.4 计算指标权重
文献[9]总结了 3种模糊一致矩阵排序的方法,并从运算复杂度与分辨率大小的角度进行了对比分析,认为文献[10]给出的排序方法科学合理,但文献[11]研究认为将运算复杂度作为评价依据不合适,且通过引入参数实现了分辨率大小可调。在模糊层次分析法中,分析目的是通过对比评价得出最优方案,所得指标权重仅具有相对意义,其数值没有实际的物理意义。此外,文献[9]的研究表明 3种排序方法得出的排序结果是相同的。故此处选用按行求和归一化法[12]计算指标权重。
指标 fi对上层因素A的指标权重为:
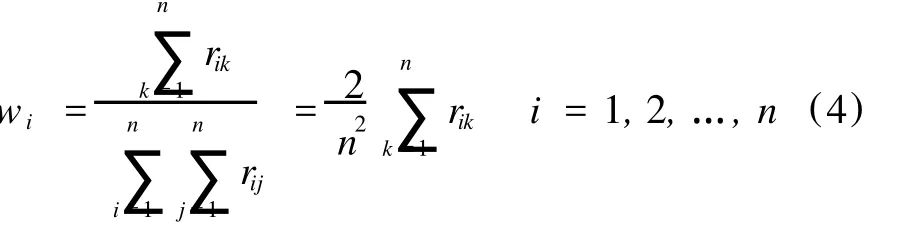
通过层次单排序得出准则层、方案层中各指标对上层因素的指标权重后,将方案层因素的指标权重分别与准则层诸因素的指标权重相乘、再求和即可得到各方案的综合指标权重。综合指标权重最大者对应方案为最优方案。
2 宜昌长江盾构穿越的机型优选
2.1 穿越工程概况
宜昌长江盾构穿越地处“川气东送”管道宜昌云池江段,工程主要由北岸始发井、南岸接收井与盾构隧道 3部分组成。北岸始发井位于湖北省宜昌市猇亭区方家岗村,南岸接收井位于宜都市红花套镇光明村。隧道总长 1405 m,掘进地层由粘土质粉砂岩、砂卵砾石层及少量粉砂层构成(见图 2),地质条件复杂,刀具磨损严重、刀具被粘土包裹、掘进地层失稳坍塌等是此类地层掘进中易出现的难点问题。为顺利克服这些困难,针对工程条件选用最优盾构机型成为工程建设的首要问题。

图2 宜昌盾构施工中从江底取出的卵石
2.2 建立递阶层次模型
根据图 1中的盾构机型分类,方案层应包括 6项因素,分别记为土压平衡式盾构机 (C1)、泥水平衡式盾构机 (C2)、挤压式盾构机 (C3)、全敞胸机械式盾构机 (C4)、全敞胸半机械式盾构机 (C5)、全敞胸手掘式盾构机(C6)。依据宜昌穿越的工程特点,结合文献[2]~[4]中介绍的盾构选型实践经验,确定土层适应性 (B1)、挖掘面稳定性 (B2)、推进速度(B3)、环境影响 (B4)、工程投资 (B5)五项评价标准作为准则层的组成因素。目标层为适应宜昌盾构穿越工程的最优盾构机型 (A)。根据上述分析,图 3给出了所建立的递阶层次模型。

表1 A-Bi优先关系矩阵
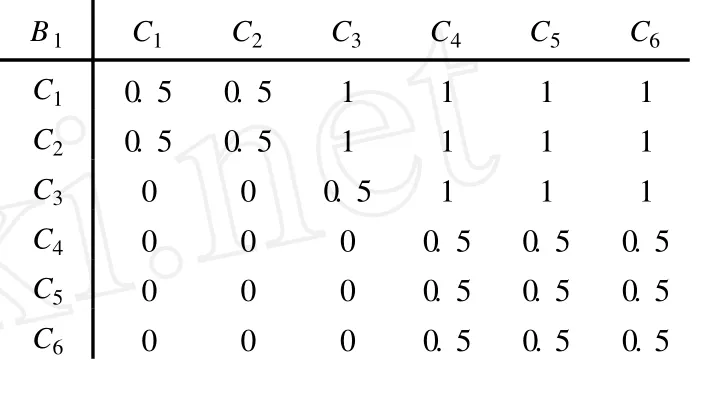
表 2 B1-Ci优先关系矩阵
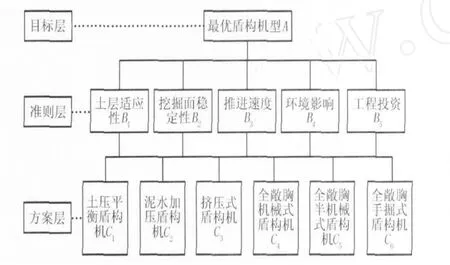
图3 盾构机型优选的递阶层次模型
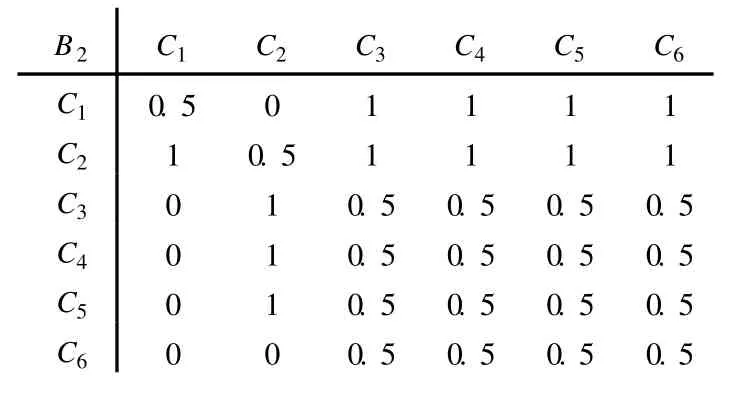
表 3 B2-Ci优先关系矩阵
2.3 得出优先关系矩阵
首先看准则层诸因素对目标层的优先关系。在宜昌穿越工程中,土层适应性与挖掘面稳定性直接关系到穿越工程的成败,属最优先考虑的第一梯次因素;考虑到工期要求与节省工程开支,将推进速度与工程投资列为第二梯次因素;在保证施工措施正常进行的情况下,穿越工程对环境影响较小,将环境影响作为第三梯次因素。根据上述分析得出准则层对目标层A的优先关系矩阵(表 1)。表 2~表 6给出了方案层诸因素对准则层的优先关系矩阵,以方案层对上层因素 B1的优先关系矩阵为例说明优先关系的确定方法。宜昌穿越地层主要由粘土质粉砂岩与砂卵砾石层构成,隧道断面岩性分布不均匀且有明显差异,掘进处地下水压大,最高达 0.36 MPa。结合盾构机型的工作原理与结构特点[1],土压平衡盾构机与泥水平衡盾构机对宜昌穿越地层有良好的适应性,可作为第一梯次因素;挤压式盾构机可适应高含水地层,但穿越地层的流塑性较差、地下水压高,将其定位于第二梯次因素;由于穿越处无法采取降排水措施,故难以采用 3种全敞胸式盾构机,列为第三梯次因素。根据上述优先关系确定方案层对B1的优先关系矩阵如表 2所示。
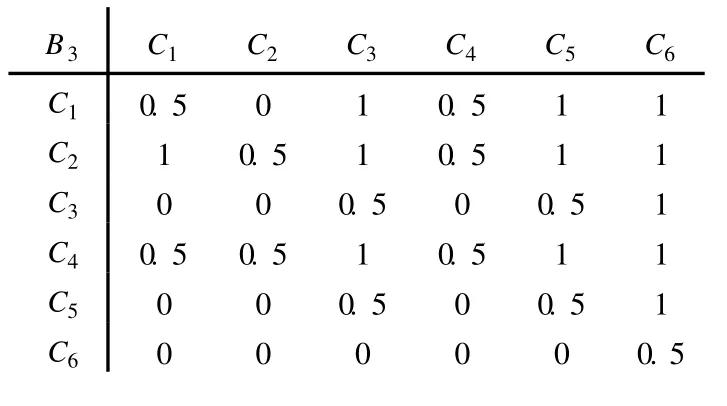
表 4 B3-Ci优先关系矩阵
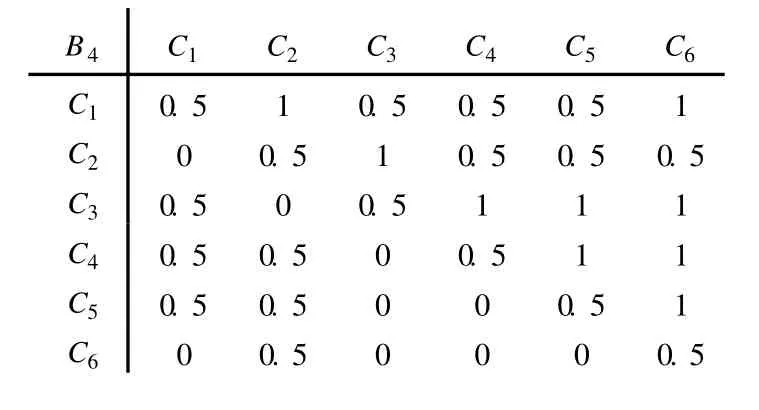
表 5 B4-Ci优先关系矩阵
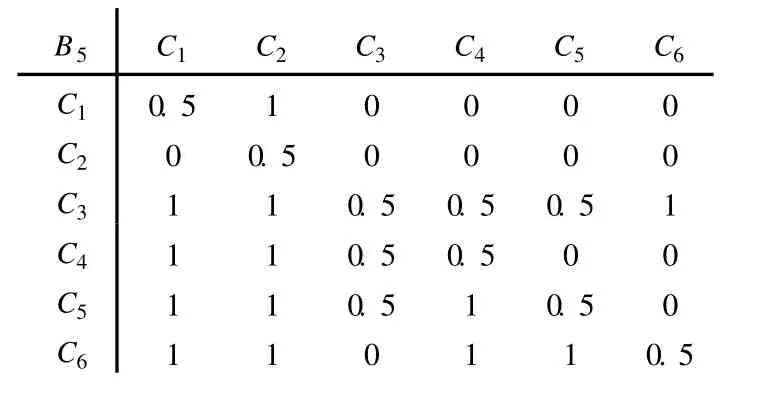
表 6 B3-Ci优先关系矩阵
2.4 计算指标权重
2.4.1 层次单排序
根据公式(2)、(3)将 A-Bi优先关系矩阵改造为模糊一致矩阵 RA-Bi(表 7),再通过公式 (4)可求得准则层诸因素Bi对A的指标权重:
WA-Bi={0.26,0.26,0.18,0.12,0.18}
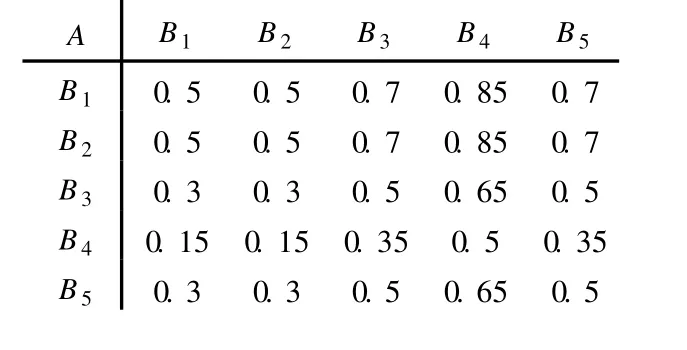
表7 A-Bi模糊一致矩阵
按照同样步骤可得方案层诸因素 Ci对准则层的指标权重。汇总各指标权重如表 8所示。
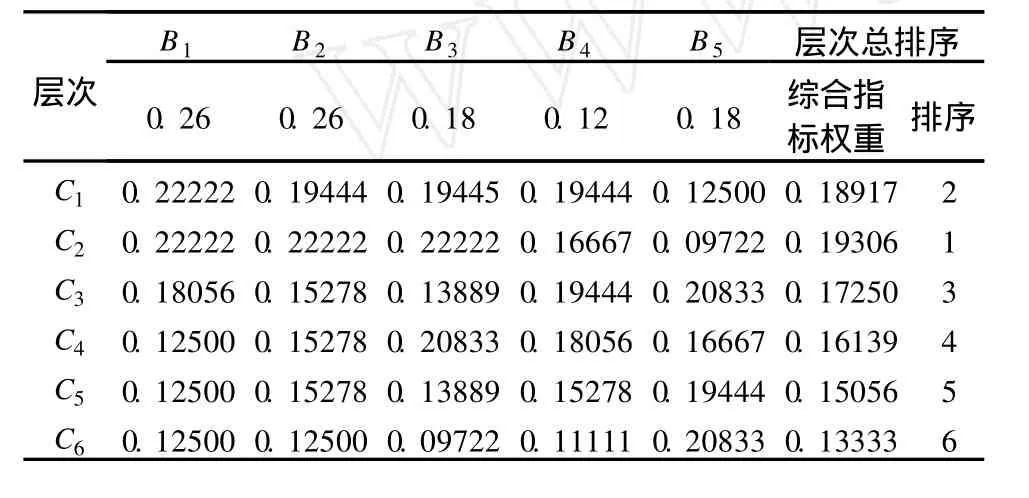
表8 各层次指标权重与综合指标权重
2.4.2 层次总排序
方案层 C1的综合指标权重为:
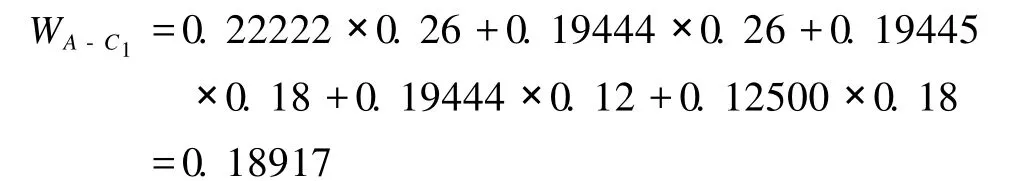
按照同样计算方法得出其他方案的综合指标权重,如表8中所示。
根据表 8中综合指标权重的计算结果,C2的综合指标权重最大,宜昌盾构穿越采用泥水平衡盾构机最优。工程实际中使用德国海瑞克公司制造的AVND3080AH复合式泥水平衡盾构机(该套设备刚成功完成广东LNG珠江穿越的隧道施工[13]),刀盘外径 3809 mm,工作性能稳定,按质按期完成了宜昌盾构隧道工程的掘进工作,且创造了连续掘进 635 m卵石层的国内最长记录。
3 结论
本文总结给出了模糊层次分析法的分析步骤,并将其应用于盾构机型的优选。通过宜昌长江盾构穿越的盾构机型优选应用实例,详细给出了分析中所需参数的确定方法及优选结果的计算过程,研究中得出以下结论:
(1)建立递阶层次模型是模糊层次分析法的关键环节,模型中准则层诸因素的提炼是否不漏不多不偏直接影响方案层的排序结果。
(2)指标权重仅具有相对意义,用于对比排序,其数值没有实际的物理意义。文献[2]总结的 3种排序方法所得排序结果相同,分析中均可采用。
(3)宜昌长江盾构穿越的盾构机型优选实例表明将模糊层次分析法应用于盾构机型优选可行有效,可在盾构穿越工程中推广应用。
[1] 王梦恕.不同地层条件下的盾构与 TBM选型[J].隧道建设, 2006,26(2):1-3,8.
[2] 宋克志,朱建德,王梦恕,等.无水砂卵石地层盾构机的选型[J].铁道标准设计,2004,(11):51-54.
[3] 陶建勋,段浩,孙凤革,等.对富水砂卵石地层盾构机选型的思考[J].现代城市轨道交通,2009,(3):70-72.
[4] 张松杰.浅谈盾构的选型与关键参数的选择[J].山西建筑, 2009,35(10):140-141.
[5] 陈营,汪玉春,陈燕彬,等.模糊层次分析法在管道线路优选中的应用[J].油气储运,2009,28(5):28-31.
[6] 沈华,马保松,吴浪辉,等.水平定向钻穿越工程的项目风险评价[J].探矿工程(岩土钻掘工程),2010,37(3):62-65,81.
[7] 姚敏,张森.模糊一致矩阵及其在软科学中的应用[J].系统工程,1997,15(2):54-57.
[8] 姚敏,黄燕君.模糊决策方法研究[J].系统工程理论与实践, 1999,(11):61-64,70.
[9] 张吉军.模糊一致判断矩阵 3种排序方法的比较研究[J].系统工程与电子技术,2003,25(11):1370-1372.
[10] 吕跃进.基于模糊一致矩阵的模糊层次分析法的排序[J].模糊系统与数学,2002,16(2):79-85.
[11] 兰继斌,徐扬,霍良安,等.模糊层次分析法权重研究[J].系统工程理论与实践,2006,(9):107-112.
[12] 徐泽水.模糊互补判断矩阵排序的一种算法[J].系统工程学报,2001,16(4):311-314.
[13] 李勇成,张志鹏,陈绍友.泥水平衡盾构在粘土层中的掘进技术[J].探矿工程(岩土钻掘工程),2008,35(2):75-76,71.
Application of Fuzzy Analytical Hierarchy Process(FAHP) in the Opt imum Selection of Shield Machine
CA I Li2 ang2xue1,HE Li2m in1,LV Yu2ling1,ZHANG De2qiao2,CHEN Xue2hua2(1.College of Pipeline and Civil Engineering, China University of Petroleum,Qingdao Shandong 266555,China;2.Sinopec Pipeline Storage and Transportation Compa2 ny,Xuzhou Jiangsu 221000,China)
Selection of the appropriate shield machine to fit complex layers and construction requirements is critical for shield crossing projectswhile it is finished qualitatively according to construction experience at present.The paper presents that the fuzzy analytical hierarchy process(FAHP)and the optimum selection of shield is done in terms of qualitative eval2 uation and quantitative calculation by 3 stepswhich include establishing the hierarchicalmodel,determining the fuzzy con2 sistentmatrix and calculating indexweights.The successful application of FAHP in Yangtze River shield crossing project in Yichang shows that the essential part of FAHP is the establishment of hierarchicalmodel.The comprehensive indexweight whose value has no real physicalmeaning is only used for comparing and sorting.
FAHP;shield;optimization;matrix;weight
TE973.9;U455.43
A
1672-7428(2011)05-0070-04
2010-12-02
蔡亮学(1984-),男(汉族),山东临朐人,中国石油大学(华东)博士研究生,油气储运工程专业,主要从事非开挖施工技术研究,山东省青岛市黄岛区长江西路 66号中国石油大学储建学院博 08,cailiangxue-184@163.com。

