多模跟踪技术在轮式侦察车图像处理器的应用
郝志成,高 文,2
(1.中国科学院长春光学精密机械与物理研究所,吉林长春130033; 2.中国科学院 研究生院,北京100039)
1 引言
目标跟踪[1-3]是通过人工或计算机自动选取感兴趣目标,然后在每一帧图像中找到选定目标,并标示出来的过程。在实际应用中,跟踪器处理的实时图像都是由可见光CCD或红外照相机等拍摄采集的,由于装配跟踪器的载体处于运动状态,跟踪器本身的振动亦会造成每一帧的图像光照变化,所以视场视角变化很大;另外,目标不同角度的旋转形变,以及周围环境的烟雾、遮挡、阻塞等情况,都给跟踪器的工作带来了很多困难,这些已成为目标跟踪急需解决的难题[4-6]。
目前目标跟踪[7-9]有相关跟踪、重心跟踪等在工程上应用非常成熟的算法[9-10],这些算法可根据处理方式不同分为基于匹配的算法、基于检测的算法、基于概率预测的算法等。
基于匹配的算法即通过对每帧图像采用各种类型的特征模板(如Harris特征角点、尺度不变特征变换(Scale-Invariant Transform Feature,SIFT)特征点[11-12]、目标边缘特征、目标核直方图[13]等)进行匹配来实现目标跟踪,这种方法不能很好地解决目标遮挡等问题。
基于检测的方法是利用运动估计[14]、光流法[15]、背景差分法[16]等进行图像分割从而实现目标跟踪。从直观上理解对于检测首先必须有目标,所以该方法也不能很好地解决目标遮挡问题。
基于预测的方法是采用概率论思想对目标的位置进行预测,从而实现跟踪,比较典型的有卡尔曼滤波[12]、粒子滤波[13]等。这种方法对遮挡有很好的鲁棒性,但需要与其他方法配合使用。
针对上述难题,本文对粒子滤波和SIFT算法进行了改进,并将多种跟踪算法相结合,提出了多模跟踪技术,通过实验验证解决了上述难题,该项技术在轮式侦察车图像处理器中得到了应用,应用效果理想。
2 跟踪状态的具体分析
目标跟踪过程中出现的目标遮挡和丢失问题是常见的,本文对遮挡和丢失的特点进行了分析。
若以原始目标与当前帧计算得到的目标的相关系数作为度量,那么出现遮挡和丢失时会使相关系数降低,但两者的具体表现又有着明显不同。
对于动目标,遮挡出现时,相关系数开始降低,并随着遮挡部分增大而继续下降,当达到一个最大值之后,目标渐渐离开遮挡,相关系数又逐渐增大直至相对稳定。由此可见,连续帧遮挡问题的特点是相关系数先逐渐减小后逐渐增大。
对于动目标,丢失出现时,相关系数降到很低,并且对于连续帧,其相关系数相对稳定地保持在比较低的水平上,直至目标被重新捕获进行跟踪时相关系数才会增大到较大值。可见,对于目标丢失情况,相关系数会连续数帧都保持在较低水平上而未发生高低变化。
对于光照变化问题,战场上光线随时都在变化,反映到图像上就是像素的灰度值在不断变化,即使是同一个物体,在不同帧图像中的像素值也不尽相同。
对于目标旋转变形问题,战场目标多是在运动行进,这样图像拍摄角度的不同导致同一物体成像也是不同的,因此图像中目标的变化也是跟踪中的一大难题。
3 多模跟踪算法
本文针对目标跟踪亟待解决的问题,提出了决策主导模式的多模跟踪方法。
3.1 粒子滤波
粒子滤波[18]是蒙特卡洛思想[19]在目标跟踪中的应用,核心思想是用某一概率分布采样得到的随机样本及相应的概率分布来表示待求的后验分布,样本数趋于无穷大时,算法无限逼近真实分布,得到的结果将无限接近最优解,即基于随机抽样原理,用随机样本来模拟目标的后验状态分布。对于N个相互独立且具有相同数学期望和方差的随机变量,当N→∞时,随机变量的算术平均值以概率收敛于数学期望μ,对任意给定的整数ε,恒有:

用蒙特卡洛滤波算法进行目标跟踪[20],实质上就是用一系列随机样本求解目标后验分布的问题,在整个求解过程中主要思想是解决贝叶斯框架下的先验概率和后验概率的求解问题,对于后验概率的求解,蒙特卡洛思想采用了重要性采样[14]的方法,这是蒙特卡洛实现的核心。
贝叶斯框架的原理由“预测”和“更新”两大步骤组成,先用系统的状态转移模型来预测目标的先验状态分布,再用观测值来修正先验状态分布,得到更新后的结果,即后验状态分布,得到状态的最优估值。目标跟踪可在贝叶斯框架下抽象为如下数学模型:
分别用Xk,Zk表示第k帧的运动状态和观测状态,
状态预测:
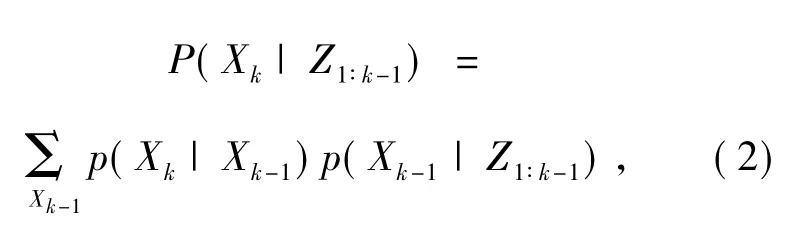
状态更新:
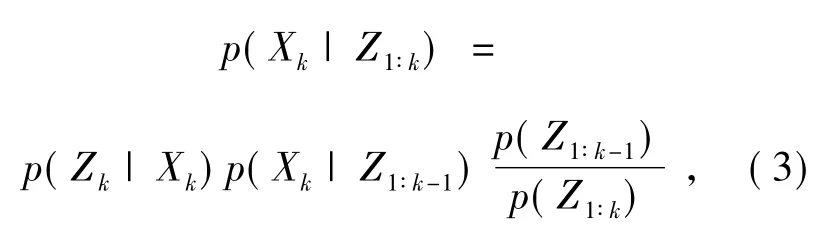
式中:P(Xk|Z1∶k-1)是先验概率,即通过过去和现在预测未来,p(Xk|Z1∶k)是后验概率,即k时刻的值已经实际得到(观测值Z1∶k),在此条件下得到之前k时刻预测状态的概率。
重要性采样定理:对于很难进行采样的p(Xk|Z1∶k,寻找一个合适的参考分布,该分布是一个已知分布q(Xk|Z1∶k)并且容易采样,称q(Xk|Z1∶k)是重要性函数,则有:

其中权重系数为:

由此可用如下公式近似求得后验概率:
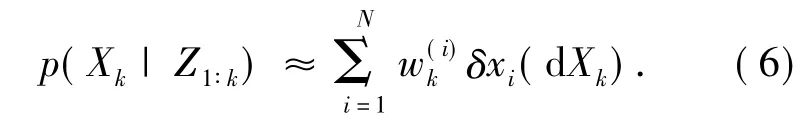
本文采用半采样半重采样的方法解决粒子滤波中的粒子退化和粒子贫瘠问题。
3.2 SIFT特征点匹配
近几年来,在计算机视觉领域,基于局部不变量描述子(Local Invariant Descriptor)的方法在目标识别和匹配方面取得了显著进展。Mikolajczyk和Schmid[16]针对不同的场景,对光照变化、图像几何变形、分辨率差异、旋转、模糊和图像压缩等6种情况,用多种具有代表性的描述子(如SIFT,矩不变量,互相关等10种描述子)进行了实验和性能比较,结果表明:在以上各种情况下,SIFT描述子的性能最好。
SIFT 算法由 D.G.Lowe1999 年提出[11],2004年完善总结[12]。SIFT是一种提取局部特征的算法,在尺度空间寻找极值点,提取位置,尺度,最后生成旋转不变量。SIFT算法步骤为:对图像进行多尺度高斯差分;建立高斯差分金字塔,即生成尺度空间;检测尺度空间极值点、精确定位极值点,为每个关键点指定方向参数;最后生成关键点描述子。该算法的优势是特征点丰富,对于旋转、放缩、亮度变化有很好的鲁棒性;缺点是计算复杂度高、计算量大,难以满足实时要求。
针对SIFT算法计算量大的问题,本文采用文献[22]提出的盒形滤波器来代替SIFT算法中的高斯滤波,盒子滤波器原理是利用各像素的积分图像,乘以不同的权重加、减得到滤波结果。两种滤波器示意图如图1所示。

图1 滤波器示意图Fig.1 Sketch maps of filters
SIFT算法中使用的高斯滤波如下:

式中:G(x,y,σ)是尺度可变高斯函数,(x,y)是空间坐标,σ是尺度坐标:
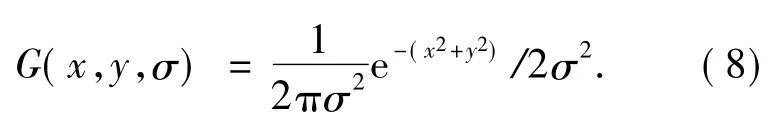
为了在尺度空间有效地检测到稳定的关键点,提出了利用不同尺度的高斯差分核与图像卷积生成的高斯差分尺度空间(DOG scale-space):

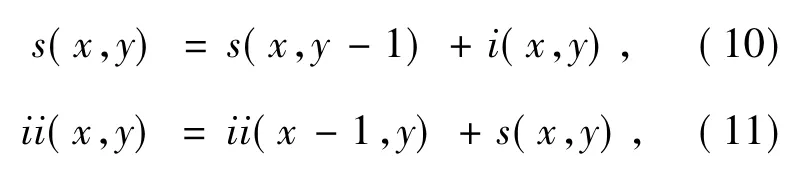
图像任意点(x,y)的积分图像用ii(x,y)表示(见图2),公式为ii(x,y),式,y'≤y中i(x',y')表示图像中点(x',y')的灰度。ii(x,y)可以用式(10)、(11)迭代计算得到:其中:s(x,y)表示一列图像的积分,且s(x,-1)=0,ii(-1,y)=0。求积分图像只需遍历一次图像,计算开销很小。如图2所示,不管窗口D的大小如何,它的灰度值总和都可以用1,2,3,4点的积分图像计算出来,即4+1-(2+3)。
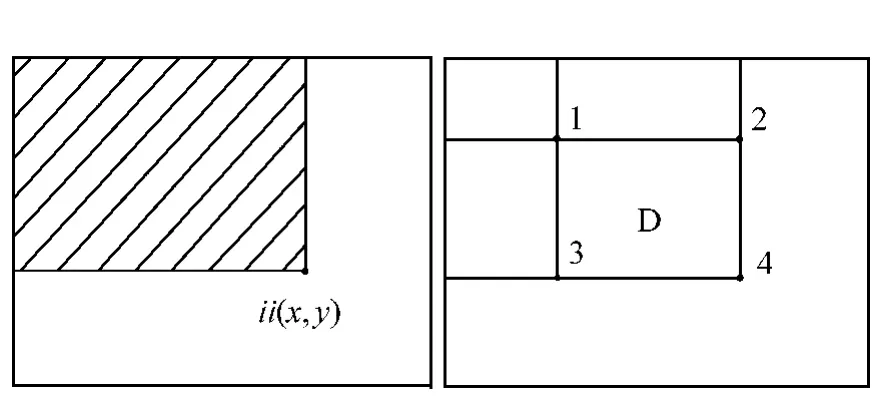
图2 积分图计算示意图Fig.2 Sketch maps of calculating integral picture
盒形滤波器计算量不随计算窗口的增大而增大,而高斯滤波的计算量随窗口的增大而成倍增长,这使得采用盒形滤波器计算量大幅降低。

图3 试验图片Fig.3 Experimental images
图3 为试验用的图片。传统SIFT算子一阶金字塔匹配结果如图4所示(一阶金字塔不对图像的行、列向下采样),其计算量大幅降低,同时特征点数也大幅降低。

图4 传统SIFT算子一阶金字塔匹配结果Fig.4 Matching results of traditional SIFT 1-step pyramid
多次测试实验及分析发现,一阶金字塔匹配特征点的减少是由于采用不同尺度的滤波后,各图像并不在相同灰度级上,采用归一化可有效解决此问题,试验结果如图5所示。

图5 改进后一阶金字塔匹配结果Fig.5 Matching results of improved SIFT 1-step pyramid
3.3 本文算法
本文提出了决策主导模式的多模跟踪方法,采用相关系数作为决策判据,默认情况下采用重心跟踪预定位,若此时得到的目标与原始目标相关度高,则直接输出目标位置;若相关度低,则认为目标发生遮挡、变形,从而进行粒子滤波粗定位,重新计算此时的相关度,用SIFT进行精匹配。
目标跟踪算法实现的具体过程如下:
(1)初始化目标信息,包括确定目标位置、目标大小以及一些其他特征信息。
(2)采用重心跟踪,计算得到粗略的目标位置。
(3)计算重心跟踪得到的目标与原始目标的相关系数:
a.若相关系数μ1>60%,则重心跟踪计算得到的位置即目标位置,跳转到(5);
b.若 μ1<60%,则跳转到(4)。
(4)采用粒子滤波计算目标位置,重新计算此时得到的目标与原始目标的相关系数μ2:
若μ2>60%,认为重新找到目标;
若40% <μ2<60%,计算粒子滤波得到的位置周围M·M(M<W/2,M<H/2)的矩形区域内的SIFT特征点并与原始目标的SIFT特征点进行匹配,得到精确位置,若匹配失败,认为目标彻底丢失或阻塞。
(5)输出计算得到的目标位置。
(6)若μ1>60%,下一帧时从步骤(2)开始重新计算;
若 μ1<60%,μ2>60%,下一帧从步骤(2)开始重新计算;
若μ1<60%,40% <μ2<60%,下一帧从步骤(4)开始重新计算;
若μ1<60%,μ2<40%,且已连续10帧均出现此种情况,认为目标丢失;否则认为目标暂时被阻塞,转到(4),见图6。
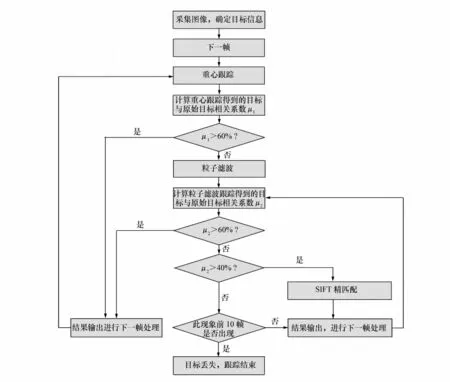
图6 本文算法的具体流程图Fig.6 Flow chart of the algorithm in this paper
4 实验结果
图7是对运动汽车进行的目标跟踪法实验,可以看出该算法对于目标的旋转形变(第1帧到209帧目标旋转近80°)、遮挡(第31帧到89帧)等情况都有非常好的鲁棒性。
图8是利用本算法在一轮式侦察车图像处理器上进行试验得到的一组图片,可以看出该算法对战场环境下的烟雾、遮挡、目标旋转形变都有很好的适应性。

图7 实验结果Fig.7 Experimental results

图8 实验结果Fig.8 Experimental results
5 结论
本文提出了决策主导模式的多模跟踪技术,分别对粒子滤波和SIFT算法做了改进,使其满足实施性要求,并找到了合理的切入点,将两者结合从而实现更加鲁棒的跟踪方法。通过实验论证了该技术对目标旋转形变、遮挡、光照变化具有鲁棒性。
[1]王选贺,刘济林.基于核密度估计的遮挡人体跟踪[J].浙江大学学报(工学版),2011,45(3):412-418.WANG X H,LIU J L.Tracking human under occlusion based on kernel density estimation[J].J.Zhejiang University(Engineering Science),2011,45(3):412-418.(in Chinese)
[2]赵丰,汤磊,陈国友,等.RBPF粒子滤波在目标跟踪中的应用研究[J].计算机工程,2011,37(3):149-151.ZHAO F,TANG L,CHEN G Y,et al..Research on application of RBPF in target tracking[J].Computer Eng.,2011,37(3):149-151.(in Chinese)
[3]陈爱华,孟勃,朱明,等.多模式融合的目标跟踪算法[J].光学 精密工程,2009,17(1):185-190.CHEN A H,MENG B,ZHU M,et al..Multi-pattern fusion algorithm for target tracking[J].Opt.Precision Eng.,2009,14(9):1745-1749.(in Chinese)
[4]薛陈,朱明,陈爱华.鲁棒的基于改进Mean-shift的目标跟踪[J].光学 精密工程,2010,18(1):234-239.XUE CH,ZHU M,CHEN A H.Robust object tracking based on improved Mean-shift algorithm[J].Opt.Precision Eng.,2010,18(1):234-239.(in Chinese)
[5]李焱,陈涛,曹立华,等.舰载光电设备跟踪掠海目标的控制[J].光学 精密工程,2010,18(4):935-942.LI Y,CHEN T,CAO L H,et al..Control of ship-based optoelectronic equipment for tracking near-sea targets[J].Opt.Precision Eng.,2010,18(4):935-942.(in Chinese)
[6]周斌,王军政,沈伟.基于组合带宽均值迁移的快速目标跟踪[J].光学 精密工程,2010,18(10):2297-2305.ZHOU B,WANG J ZH,SHEN W.Fast object tracking with multi-bandwidth Mean Shift[J].Opt.Precision Eng.,2010,18(10):2297-2305.(in Chinese)
[7]苑玮琦,董茜,桑海峰.基于方向梯度极值的手形轮廓跟踪算法[J].光学 精密工程,2010,18(7):1675-1683.YUAN W Q,DONG Q,SANG H F.Hand shape contour tracking method based on directional gradient extremum[J].Opt.Precision Eng.,2010,18(7):1675-1683.(in Chinese)
[8]李忠海,王莉,崔建国.基于Camshift和Particle Filter的小目标跟踪算法[J].计算机工程与应用,2011,47(9):192-195,199.LI ZH H,WANG L,CUI J G.Weak aerial target tracking algorithm based on camshift and particle filter[J].Computer Eng.Appl.,2011,47(9):192-195.(in Chinese)
[9]蔺海峰,马宇峰,殷璇,等.基于SIFT特征的抗遮挡目标跟踪算法[J].计算机工程,2011,37(4):198-200.LIN H F,MA Y F,YIN X,et al..Anti-occlusion object tracking algorithm based on SIFT feature[J].Computer Eng.,2011,37(4):198-200.(in Chinese)
[10]朱向军,毛剑飞,鲍卫兵.基于达芬奇技术的智能视频监控终端的开发[J].电信科学,2011(2):100-104.ZHU X J,MAO J F,BAO W B.Development of intelligent visual surveillance device based on davinci[J].Telecom Sci.,2011(2):100-104.(in Chinese)
[11]LOWE D G.Object recognition from local scale-invariant features[C].The 7th International Conference on Computer Vision,Kerkyra,Greece,20-27 Sept.1999:1150-1157.
[12]LOWE D G.Distinctive iImage features from scale-invariant keypoints[J].International J.Computer Vision,2004,60(2):91-110.
[13]COMANIEIU D,MEER P.Distribution free decomposition of multivariate data[J].Pattem Anal.Appl.,1999,2(1):22-30.
[14]MURRAY D W,BUXTON B E.Scene segmentation from visual motion using global optimization[J].IEEE T.Pattern Anal.,1987,9:220-228.
[15]MARKANDEY V,REID A,WANG S.Motion estimation for moving target detection[J].IEEE T.Aero.Elec.Sys.,1996,32(3):866-874.
[16]STAUFFER C,GRIMSON E.Learning patterns of activity using real time tracking[J].IEEE T.Pattern Anal.,2000,22(8):747-757.
[17]KALMAN R E.A new approach to linear filtering and prediction problems[J].Transaction ASME-J.Basic Eng.,1960,82(Series D):35-45.
[18]GORDON N J,SALMOND D J,SMITH A F M.Novel approach to nonlinear and non-Gaussian bayesian state estimation[J].IEEE Proceedings-F,1993,140(2):107-113.
[19]ISARD M,BLAKE A.Condensation-conditional density propagation for visual tracking[J].International J.Computer Vision,1998,29(1):5-28.
[20]孟勃,朱明.采用EM算法对粒子滤波跟踪算法进行改进[J].中国图象图形学报,2009,14(9):1745-1749.MENG B,ZHU M.The application of EM algorithm to improve particle filter[J].J.Image and Graphics,2009,14(9):1745-1749.(in Chinese)
[21]MIKOLAJCZYK K,SCHMID C.A performance evaluation of local descriptors[J].IEEE T.Pattern Anal.,2005,27(10):1615-1630.
[22]BAY H,TUYTELAARS T,GOOL L V.SURF:Speeded up robust features[J].Computer Vision and Image Understanding,2006,110(3):346-359.

