考虑负荷需求弹性的输电阻塞管理①
何 艺, 王 健, 李婷婷
(华南理工大学电力学院, 广州 510640)
考虑负荷需求弹性的输电阻塞管理①
何 艺, 王 健, 李婷婷
(华南理工大学电力学院, 广州 510640)
在输电阻塞管理中考虑负荷的需求弹性(load demand elasticity),并研究不同需求弹性对系统阻塞程度、节点需求电价和系统网损的影响。文中的模型是以社会收益最优为目标函数,考虑负荷需求弹性以及各种系统约束条件,通过路径跟踪内点算法求解最优潮流(OPF),利用电价经济杠杆调节用户用电。通过IEEE-14母线系统算例验证了高需求弹性能有效缓解输电阻塞,减少阻塞费用,使潮流分布更合理和公平。
电力市场; 输电阻塞; 负荷需求弹性; 最优潮流; 内点算法
电力市场改革的主要目标是通过引入市场竞争来降低成本、提高效率,促进电力系统长期稳定发展。电力市场中的输电网开放、大区联网、分散自主报价和双边自主交易、跨区域电能交易等,与垄断环境下相比,更容易导致输电阻塞。输电阻塞(transmission congestion)一般包括两种情况:
①输电线路或变压器潮流超过允许极限;
②节点电压越限。
现在合理解决输电阻塞的手段有二大类[1]:一类是电网公司通过调整网络结构和控制器参数改变网络潮流,避免更改发电计划及由此引起的附加阻塞费用;另一类是以经济性为目标,在各种交易模式下采用不同的目标函数,根据最优潮流OPF分布[2~4]调整输电计划来消除阻塞,同时考虑系统常规约束,其中最具代表性的有节点电价法[5,6]。根据“实时电价”原理确定潮流分布,往往导致发电商和用户承担的阻塞费用及电价波动都太大,对运行条件和网络特性也相当敏感,并且还存在较大的交易盈余。
节点电价包含能量的生产成本、输电阻塞成本以及网损成本,文献[5]根据经典实时电价理论推导出节点电价的网损修正公式,并从中定义了网损修正系数。文献[7]在输电阻塞管理中考虑了系统暂态稳定约束,提出了一种考虑预想事故下暂态稳定约束的动态阻塞管理算法。文献[8]利用潮流跟踪方法分析引起输电阻塞的责任,并充分考虑负荷需求弹性的影响,根据用户的需求曲线提出一种定价方法。文献[9]利用灵敏度分析与线性规划提出了一种超短期在线阻塞管理的数学模型及算法。总之,输电阻塞管理的问题在于,如何确定阻塞管理模型即目标函数以及各类约束以达到目标最优,如何合理分配阻塞费用以期尽可能调动各发电商和用户的积极性,从长远角度来保证电力市场的健康稳定运行。
市场环境下,电力作为一种商品,必然存在需求弹性(load demand elasticity)。传统电力体制下电能商品的需求弹性几乎为完全刚性,这是由电能商品的物理特性与竞价市场的交易模式两方面原因共同造成的。随着电力市场的发展,尤其在销售侧开放的市场模式下,用户的需求弹性显著增大,并将呈现多样化。需求弹性可以通过多种途径获得,如购电商自由报价、可中断负荷等[10],在电力市场中引入需求弹性的研究也越来越多[10~12]。
本文中,在最优潮流计算过程中考虑用户的需求弹性,负荷不再是固定的,而是一条体现用户购买意愿的需求曲线。需求曲线代表用户在特定电价下愿意购买的负荷电量。考虑需求弹性后,利用经济杠杆调节用户负荷,能更有效地缓解输电阻塞,减少交易盈余。
1 模型的基本思想
电力市场环境下,电网公司根据发电侧报价曲线和用户需求曲线(经济学中企业的边际成本曲线和消费者的边际效用曲线)[13],以社会收益最优为目标函数,考虑了发电机组、系统和网络安全约束条件,使用路径跟踪内点算法求解最优潮流,确定系统最终的潮流分布以及实时节点电价。
2 模型的建立
2.1 负荷需求弹性模型
需求弹性是指需求的价格弹性(price elasticity of demand),经济学定义是:一种商品需求量的相对变动对其自身价格相对变动的反应程度[13],用弹性系数e表示为
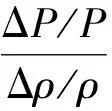
(1)
式中:ΔP/P表示需求的相对变化量;Δρ/ρ表示价格的相对变化量。

(2)

(1)当e>1,则认为富有需求价格弹性(price-elastic demand);
(2)当e<1,则认为缺乏需求价格弹性(price-inelastic demand);
(3)当e=1,则认为拥有单位需求价格弹性(unit-elastic demand);
(4)需求的极端情况是需求无弹性(e=0),以及完全有弹性(e=∞)。
假设用户需求曲线是一个关于负荷功率的线性函数为
(3)
则相应的弹性系数为
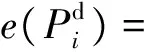
(4)
式中,b1i和b2i为系数,其中b2i<0。
2.2 最优潮流计算模型
本文以社会效益最大化为目标函数
(5)
约束条件如下。
(1)系统潮流方程为
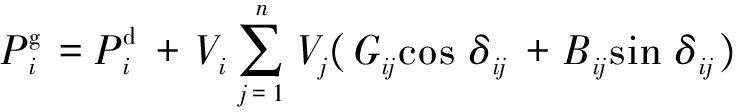
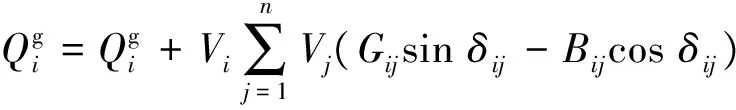
(6)
(2)发电机有功和无功出力约束为
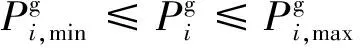
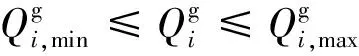
(7)
(3)输电线路的传输容量约束为
Slk,min≤Slk≤Slk,maxk∈L
(8)
(4)节点电压约束为
Vi,min≤Vi≤Vi,max
(9)
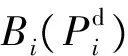
综上所述,电力系统最优潮流问题的数学模型可以表示为
s.t.minf=f(x,u)
g(x,u)=0
hmin≤h(x,u)≤hmax
(10)
式中:x是状态变量;u是控制变量;g(u,x)和h(u,x)分别对应等式约束和不等式约束条件。
2.3 路径跟踪内点算法
可以看出,电力系统最优潮流计算是一个典型的多约束非线性规划问题。本文采用文献[14]中提出的基于扰动KKT条件的路径跟踪内点算法求解该问题。这种方法的实质是通过引入松弛变量化函数不等式约束为等式约束,再通过拉格朗日乘子和库恩乘子把等式约束和不等式约束与目标函数复合,化原问题为无约束最优化问题。最后用牛顿法对其一阶最优性条件进行求解。
首先,引入松弛向量l和u化原式(10)中函数不等式约束为等式约束,构造拉格朗日函数为
L(*)=f(x)-λTg(x)-zT[h(x)-l-
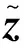
(11)
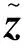
在路径跟踪法中引入一扰动变量μ作为松弛互补条件,可以推导出式子(11)的KKT条件为
Lx≡f(x)-g(x)l-
(12)
Ly≡g(x)=0
(13)
Lz≡h(x)-l-hmin=0
(14)
Lw≡h(x)+u-hmax=0
(15)
Ll≡LZe-μe=0
(16)
Lu≡UWe+μe=0
(17)
(l,u,z)≥0,w≤0,λ≠0
式中:L、U、Z、W表示元素为l、u、z、w的对角矩阵;e∈Rr,e=[1,…,1]T∈Rr。
上述扰动KKT条件可用牛顿法解开,化简后消去Δl、Δu、Δz、Δw,得到最终简约KKT系统为
(18)
其中:H(·)≡[2g(x)λ+2h(x)(z+w)-2f(x)]+h(x)(U-1W-L-1Z)h(x)T=Hg+Hh;J(x)≡g(x)T;Ψ(·,μ)≡g(x)λ-f(x)+h(x)×[U-1WLw0-L-1ZLz0-μ(U-1-L-1)e]。
式(18)中,H(·)由Hg和Hh组成;Hg是f(x)、g(x)、h(x)海赛矩阵的线性组合;Hh称为障碍矩阵,其作用是防止不等式约束h(x)违反双边极限。
可见,路径跟踪法的主要计算负荷集中在每次简约修正方程(18)的形成和求解上。
由此产生的路径跟踪法内点迭代格式如下。
(1)初始化。置迭代标记k=0,最大迭代限制次数Kmax,中心参数δ∈(0,1),收敛精度ε=10-6。选择[l,u]T>0,[z>0,w<0,y=0]T。
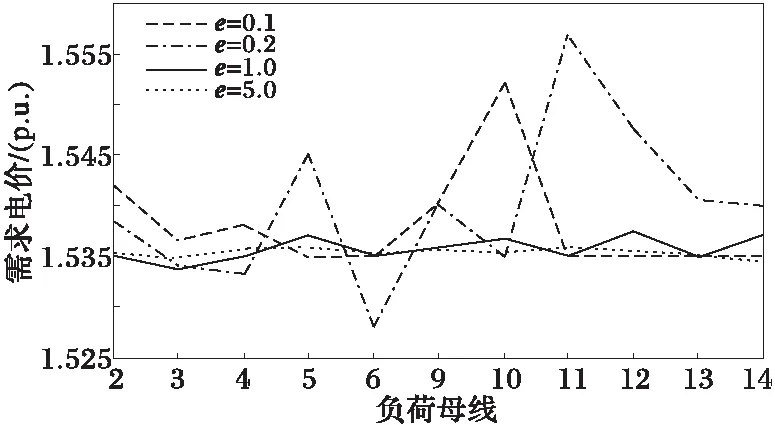
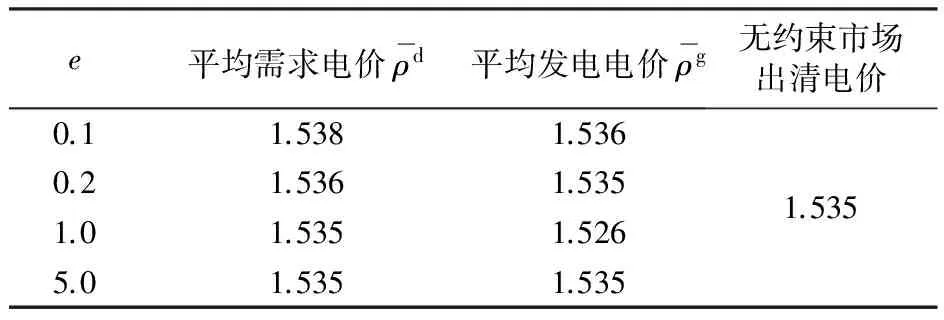
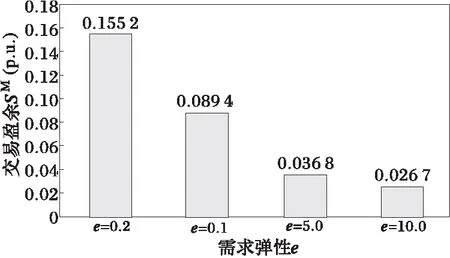
(2)如果k (3)计算互补间隙CGap:CGap≡eT(LZ-UW)e。如果CGap<ε,停止,输出最优解。 (4)求解修正系统,获取修正量[Δx,Δλ],[Δl,Δu],[Δz,Δw]。 (5)比值检验,确定原始和对偶空间中的最大步长: (19) (20) 式中:i=1,2,…,r。 (6)更新原始和对偶变量 (21) 关于路径跟踪内点发的理论推导,可参考文献[15]。 交易盈余(merchandise surplus)为 (21) 交易盈余SM是一个衡量阻塞费用的参数,是电网公司从用户收取的费用与支付给发电商费用之差;在无约束的理想市场里,SM=0;SM的绝对值越小则说明由于阻塞而多支付的费用越小,即阻塞程度越轻,潮流分布更合理和公平。 假定电网公司要制定输电计划(本文以IEEE-14母线系统为算例,见图1),系统有6台发电机,11个负荷,负荷的弹性系数可以根据统计资料和调查结果进行估算。以社会收益最优为目标函数,使用Matlab软件编写基于路径跟踪内点算法的最优潮流程序。负荷的无功功率模型使用常系数模型(与有功功率成正比),发电机组数据见表1。 图1 IEEE-14母线系统 发电机C2C1C0PgmaxPgminQgmaxQgmin10.6461.23.51.50.51.5-1.020.7181.34.11.30.20.6-0.330.5061.153.71.00.20.5-0.560.7851.354.30.80.30.4-0.380.2521.353.91.450.50.8-0.5 1)考虑系统所有母线需求弹性 忽略系统网损,假定系统所有负荷具有相同的需求弹性,母线电压都限制在0.95~1.05。计算结果如图2~图3所示。 图2 交易盈余SM和负荷电价标准差 图3 负荷节点需求电价 由图2可见,随着需求弹性系数e的增大,交易盈余SM和电价标准差是减少的。e=1.0和e=5.0情况下SM为负数,电网公司从用户得到的费用少于支付给发电商的费用。而电价标准差(图2)则衡量了不同弹性系数下的电价波动程度。 同样,图3表示不同需求弹性系数下各个负荷节点的需求电价,随着弹性系数的增大,负荷需求电价的波动减小,而且趋于市场出清电价ρ。 表2平均需求电价和平均发电电价 Tab.2 Average demand prices and average generationprices with respect to case Ap.u. 2)考虑系统单个负荷需求弹性 考虑系统网损,母线电压约束和线路输电容量约束。假定算例IEEE14母线系统线路6-13的最大输电容量是0.12(p.u.),考虑负荷母线13在不同需求弹性系数(e13=0.2,1.0,5.0,10.0)下对系统阻塞的影响(其他母线负荷需求弹性为0)。所有的母线电压都限制在0.95~1.05。计算结果如图4所示。 图4和图5说明了随着负荷13弹性需求的增大,交易盈余SM和系统总网损是逐渐减小的。 图4 负荷13不同需求弹性下交易盈余Sm 图5 系统总网损 图6 负荷需求电价 本文的模型中,通过电价的经济杠杆,调动了包括发电商,用户和联营体交易中心在内的参与者。有效缓解阻塞的关键是获得较精确的用户需求弹性,需求弹性系数越精确,实际潮流分布越接近最优潮流计算的结果,缓解阻塞的效果就越明显。为此,可以在容易形成阻塞的线路多安排需求弹性大的负荷,也可以考虑提高用户的需求弹性,通过发挥电价的经济杠杆以及最优潮流调度来缓解和消除阻塞,同时兼顾了用户的利益和电网安全稳定需要。 [1] 柯进,管霖(Ke Jin, Guan Lin).电力市场下的输电阻塞管理技术(Transmission congestion management in power market)[J].电力系统自动化(Automation of Electric Power Systems),2002,26(14):20-25,39. [2] 袁贵川,王建全,韩祯祥(Yuan Guichuan, Wang Jianquan, Han Zhenxiang).电力市场下的最优潮流(Optimal power flow under electricity market)[J].电网技术(Power System Technology),2004,28(5):13-17. [3] De Souza Alessandra Macedo, De Sousa Vanusa Alves, Da Costa Geraldo Roberto Martins. Optimal power flow: a tool for managing the transmission congestion[C]∥IEEE Power Engineering Society General Meeting,Denver,USA:2004. [4] 孙刚,余贻鑫(Sun Gang, Yu Yixin).一种新的优化潮流模型(A novel model of optimal power flow)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA ),2005,17(3):6-9,54. [5] 丁晓莺,王熙凡(Ding Xiaoying, Wang Xifan).考虑输电网络损耗的节点电价计算方法(Transmission losses modification in location marginal prices calculation)[J].电力系统自动化(Automation of Electric Power Systems),2005,29(22):14-18,44. [6] Chompoo-Inwai Chai,Yingvivatanapong Chitra,Fuangfoo Pradit,etal.Transmission congestion management during transition period of electricity deregulation in Thailand[J].IEEE Trans on Industry Applications,2007,43(6):1483- 1490. [7] 王建全,陈晓峰,杨梅强,等(Wang Jianquan, Chen Xiaofeng, Yang Meiqiang,etal).考虑暂态稳定约束下的输电阻塞管理计算(Calculation of transmission congestion management with transient stability constraints)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA ),2007,19(3):66-71. [8] 鲁丽娟,侯云鹤,吴耀武,等(Lu Lijuan, Hou Yunhe, Wu Yaowu,etal).计及用户需求弹性影响的输电阻塞解决方案研究(A research on transmission congestion management considering influence of consumers' demand elasticity)[J].电网技术(Power System Technology),2004,28(5):46-49. [9] 吴政球,朱民茂,王良缘,等(Wu Zhengqiu, Zhu Minmao, Wang Liangyuan,etal). 超短期在线输电阻塞管理模型及算法(On-line transmission congestion management model and algorithm)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA ),2007,19(6):109-113. [10]聂江洪,曾伟民(Nie Jianghong, Zeng Weimin).在电力市场中引入电力需求弹性的研究(Research on introducing electricity demand elasticity into electricity market)[J].电网技术(Power System Technology),2008,32(11):84-89. [11]贺辉,徐政,黄莹(He Hui, Xu Zheng, Huang Ying). 负荷在阻塞管理中的作用(The role of load in transmission congestion management)[J].电力系统自动化(Automation of Electric Power Systems),2003,27(17):11-14. [12]雷霞,刘俊勇,都亮(Lei Xia, Liu Junyong, Du Liang). 电力零售市场中分时零售电价的确定(Determination of time-of-use retail price in the retail market)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA ),2008,20(1):28-32. [13]Paul A S,William D N. Economics[M].7th ed.Columbus: Mc Graw Hill Press, 1998. [14]李尹,张伯明,孙宏斌,等(Li Yin, Zhang Boming, Sun Hongbin,etal). 基于非线性内点法的安全约束最优潮流 (一)理论分析(Security constrained optimal power flow based on nonlinear interior point method Part one theory analysis)[J].电力系统自动化(Automation of Electric Power Systems),2007,31(19):7-13. [15]Hua Wei, Sasaki H, Kubokawa J,etal.An interior point nonlinear programming for optimal power flow problems with a novel data structure[J].IEEE Trans on Power Systems,1998,13(3):870-877. TransmissionCongestionManagementConsideringLoadDemandElasticity HE Yi, WANG Jian, LI Ting-ting (School of Electric Power, South China University of Technology, Guangzhou 510640, China) Load demand elasticity is considered in the transmission congestion management, and the impacts of demand elasticity on degree of transmission congestion, buses demand price and system losses are investigated in this paper. The model with maximizing social surplus as the objective function uses optimal power flow (OPF) as a tool to make a scheduling. In the OPF model load demand elasticity as well as various system constraints are considered, and path following interior point method is used to solv the OPF. IEEE-14 bus system is illustrated as an example to show that the elastic load can contribute to congestion relief and lower the congestion cost through the economic levers of electricity price. power market; transmission congestion; load demand elasticity; optimal power flow(OPF); interior point method 2009-07-02 2009-10-20 TM73; F123.9 A 1003-8930(2011)01-0058-06 何 艺(1984-),男,硕士研究生,研究方向为电力市场。Email:heyi2903@gmail.com 王 健(1966-),女,副教授,研究方向为电力市场、电力系统分析运行与控制。Email:wangjian@scut.edu.cn 李婷婷(1985-),女,硕士研究生,研究方向为电力市场。Email:tingting_li23@163.com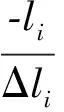
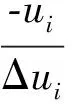
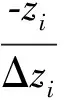
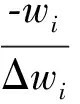
3 衡量输电阻塞程度的参数
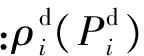
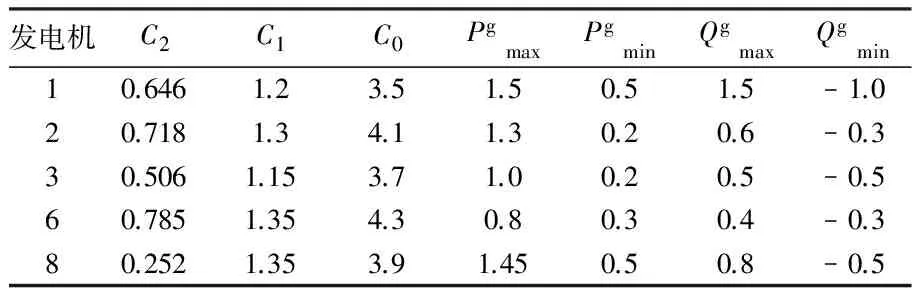
4 算例分析

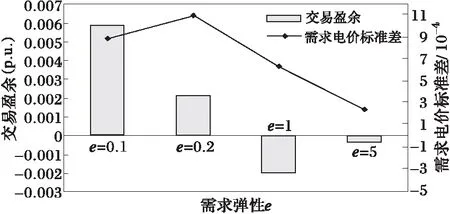
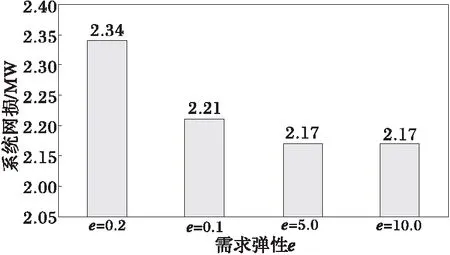
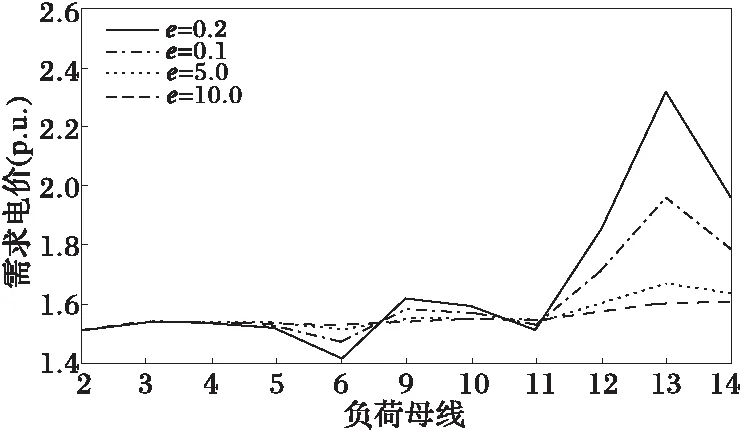
5 结语

