内点半定规划法求解含机组组合动态最优潮流

白晓清， 韦 化

(广西大学电气工程学院， 南宁 530004)

内点半定规划法求解含机组组合动态最优潮流

白晓清， 韦 化

(广西大学电气工程学院， 南宁 530004)

考虑电力系统运行的经济性和安全性，建立了含机组组合的动态最优潮流问题的半定规划模型，并采用基于半定规划的内点法直接求解。所提算法采用修正策略处理模型中的离散变量，计算时不需要进行模型分解，收敛性好，能在多项式时间内完成。为提高计算效率，采用了半定规划块状矩阵运算的稀疏技术。通过对IEEE-118节点等4个测试系统24时段的仿真计算，验证了所提方法的正确性、有效性和优越性，其研究和应用前景广阔。

动态最优潮流； 半定规划； 机组组合； 内点法

动态最优潮流问题DOPF(dynamic optimal power flow)是在满足线路容量、节点电压以及运行约束等条件下，求解一个调度周期的电力系统运行计划，并使得特定的目标函数最小[1]。其中可以调整的电力系统控制变量一般包括机组有功出力、节点电压、有载变压器变比和无功电源的无功出力。由于对离散变量的处理有一定困难，传统的DOPF问题一般不考虑机组组合问题UC(unit commitment)，因此获得的运行计划不能保证目标的最优性。为实现总运行成本最小或系统利润最大的目标，且能满足电网安全运行约束条件，有必要将机组组合问题与最优潮流问题同时考虑，通常称其为考虑机组组合的动态最优潮流问题DOPF-UC(dynamic optimal power flow with unit commitment)[2]。

从数学的角度看，DOPF-UC问题是一个高维的、非凸的、离散的、非线性的优化问题，围绕这一复杂的新问题，国内外学者提出了许多计算方法，如Benders分解法[2，3]、Lagrangian松弛法[4]、内点割平面法[5]、动态规划[6]和智能优化算法[7]等。

但由于现有算法的内在限制，上述方法存在对离散变量处理不合理、算法求解效率不稳定、需要对原问题模型分层求解等问题。本文所提内点半定规划法对离散变量采用半定松弛，不必对原模型分层求解，且算法能在多项式时间内完成，具有良好的收敛性。

半定规划SDP(semidefinite programming)[8，9]属于凸规划问题，能有效处理模型中的整数变量。经近10年发展，目前已成为数值最优化领域的研究热点。其理论研究已逐渐成熟，被成功应用于系统控制理论[10～12]，信号处理和通讯[13，14]，组合优化[15]等领域。同时，由于SDP具有良好的算法结构，许多成熟算法已被开发成接口清晰，易于调用的核心软件包[16，17]。求解相应问题不再需进行复杂的公式推导和计算，仅需按照对应关系形成问题的SDP模型，直接调用核心软件包计算。

文献[18，19]首次将半定规划应用于求解电力系统经济调度问题，效果令人满意。文献[20]采用内点半定法求解最优潮流，结果表明其全局最优性能可以得到保证。因此，将内点半定规划法引入DOPF-UC问题的求解中是一种有益的尝试。54机IEEE-118节点等4个测试系统24时段的仿真计算表明：所提方法能有效求解连续变量和离散变量，算法收敛性好，是一种应用前景广阔的方法。

1 内点半定规划法

1.1 半定规划的定义

半定规划是指线性函数在对称矩阵的仿射组合半正定约束下的极值问题，是特殊的锥优化问题，可视为线性规划的推广[9]。

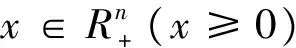
另一方面，半定规划与线性规划也有重大区别。其一，线性规划具有强对偶性，而半定规划具有弱对偶性，即具有非负的对偶间隙。其二，线性规划的向量分量不等式约束是线性和光滑的，而半定规划的线性矩阵不等式约束可以是非线性和非光滑的，但却是凸的。因此，对于某些混合整数非线性规划问题可以转换成半定规划问题。

半定规划问题有多种表达方式[9]。其中标准形式如下，分别称半定规划的原问题(Primal)和对偶问题(Dual)。

(1)

1.2 内点法解半定规划

解半定规划问题(1)等价于求解其原问题的对数障碍函数问题[8]：

(2)

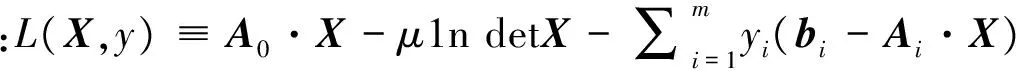
(3)

可导出其一阶最优性条件如下：

(4)

引入对称矩阵Y，可以获得如下非线性系统：

(5)

对系统(5)可导出其修正方程：

(6)

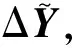
(7)

其中：

B是一个m×m的矩阵，且

Bij=(X-1AiY)·Aj，(i，j=1，…，m)；r是一个m维纵向量，且ri=-di+Ai·[X-1(R-PY)]，(i=1，…，m)。其中P，di，R分别定义为：

di=bi-Ai·Y，(i=1，…，m)

R=μI-XY

修正当前点为(X+αpΔX，y+αdΔy，Y+αdΔY)，其中αp和αd是步长因子，以保证更新后的X+αpΔX和Y+αdΔY仍在正定锥中。如此反复迭代，直到互补间隙μ=X·Y/n足够小。

当μ→0时，(X(μ)，y(μ)，Y(μ))将沿着中心路径γ(μ)≡{X(μ)，y(μ)，Y(μ)∈Rn×n×Rm×Rn×n∶μ>0}精确收敛到最优解(X*，y*，Y*)。

可以证明，内点法求解半定规划模型能在多项式时间内完成，具有超线性收敛[16]。

2 拟求解问题的半定规划模型

首先根据DOPF-UC问题的混合整数非线性规划模型，采用对离散变量进行半定松弛的方法[21]导出其凸规划模型，然后直接建立其半定规划模型。

2.1DOPF-UC的混合整数非线性模型

DOPF-UC问题可以用混合整数非线性模型表示。为方便建立其半定规划模型，本文采用如下直角坐标数学模型表示。

不失一般性，目标函数为煤耗最小的火电机组组合FCost。

(8)

同时必需满足如下约束：

1)功率平衡约束(潮流方程)

(9)

i∈SB，t∈T

2)线路约束

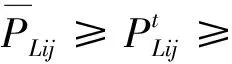
(10)

其中：

ij∈SL，t∈T

3)旋转备用约束

(11)

4)机组爬坡约束

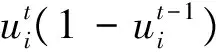
(12)

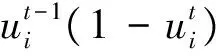
(13)

5)最小启停时间约束：

(14)

(15)

该约束为非线性的，为方便建立半定规划模型，计及机组的初始状态，可整理得与其等价的线性组合表达式如下：

(16)

(17)

6)机组有功出力上下限约束：

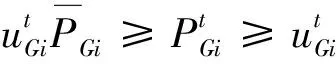
(18)

7)机组无功上下限约束：

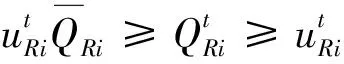
(19)

8)电压上下限约束

(20)

以上模型中各变量和下标含义如下：

T为调度周期的时段总数。

SB、SG、SR、SL分别为系统节点集合，发电机机组集合，无功电源集合和系统的线路集合，其中各集合中元素有nB、nG、nR、nL个。

PGi、QRi分别为机组i∈SG的有功功率和无功电源i∈SR的无功功率。

SRt为系统的旋转备用，取该时段负荷的10%。

FPi为燃料单价($/MBtu)。

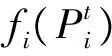
CUi为机组i∈SG的起动费用。

URi、DRi为机组i∈SG的有功爬坡费用和有功下降费用。

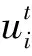
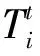
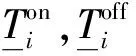
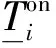
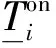
δ(t-1)为脉冲函数：

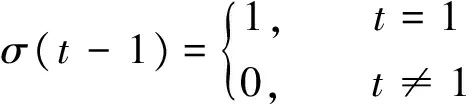
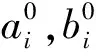
2.2DOPF-UC问题的凸优化模型

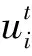
目标函数：

(21)

满足以下10种约束：

1)功率平衡约束(潮流方程)共T×nB个

i∈SB，t∈T

(22)

2)线路共2×nL个

ij∈SL，t∈T

(23)

3)旋转备用共T个

t∈T

(24)

4)机组爬坡共2×T×nG个

⟺

(25)

5)最小启停时间共2×T×nG个：

分析式(15)和(16)，除t=1的算式不一样，其他时段的可以用统一的算式表示。

当t=1时，由于，

则有：

(26)

(27)

当t=2～T时，由于

则有：

(28)

(29)

6)机组有功出力上下限共2×T×nG个：

(30)

(31)

7)机组无功上下限共2×T×nR个：

(32)

(33)

8)电压上下限共2×T×nB个：

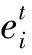
(34)

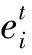
(35)

9)辅助变量约束共2×T×nG+2×T×nR个：

(36)

(37)

10)机组启停状态共2×T×nG+2×T×

nR个：

(38)

(39)

以上10种约束共有n=2nB+2nL+T(1+10nG+6nR+2nB)个。

2.3DOPF-UC问题的半定规划模型

首先定义矢量x：

t∈T

(40)

其中：①机组有功处理及其状态变量为

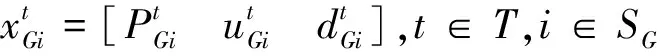
②无功源及其状态变量为

③节点电压(直角坐标)为

④松弛变量为

另外：

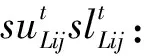
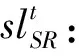
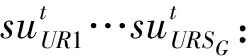
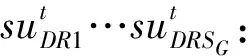
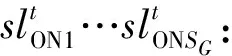
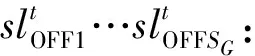
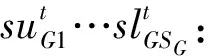
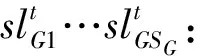
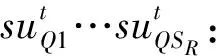
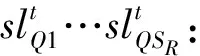
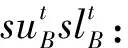
定义矩阵变量X如下：

(41)

在矩阵变量X中的XG,G为

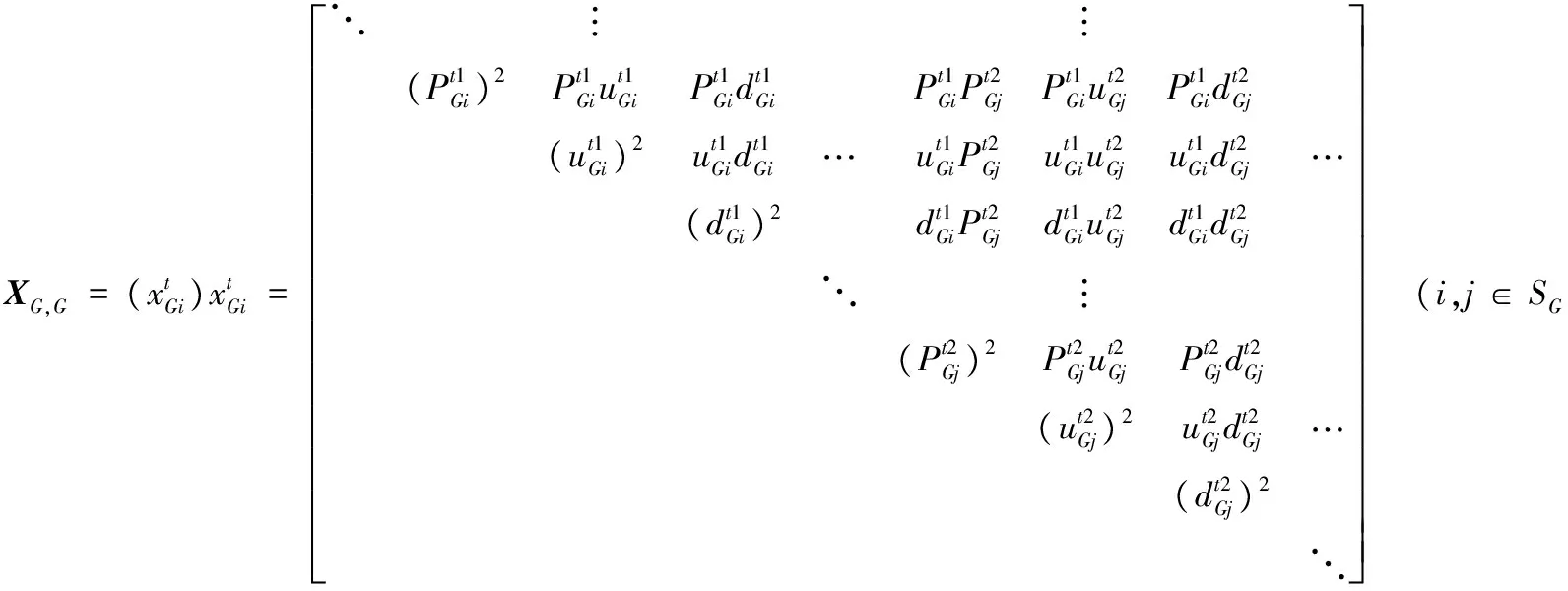
篇幅所限，且由于该矩阵变量是对称正定的[20]，这里仅列出其中XG,G子块中上三角元素以示说明。由此，根据矩阵迹的定义，可直接导出DOPF-UC问题的SDP模型原问题形式如下：

minF=A0·X

s.t.Ai·X=bi，i=1，…，n

(42)

x0

值得注意的是，按以上矢量x分组方式形成的变量矩阵具有优良的分块特性，适合采用基于分块矩阵运算的半定规划稀疏技术求解[22]，使得求解DOPF-UC问题的计算和存储效率能大幅度提高。

3 内点半定规划法求解DOPF-UC问题

采用内点半定规划法求解DOPF-UC问题的流程如图1。内点半定规划法求解DOPF-UC问题，其中离散变量存在少量非0/1解。采用一般的四舍五入处理，不能保证获得可行解。因此，为保证解的质量和可行性，本研究采用如下策略处理离散变量，列于图2。图2是对图1中虚线部分的进一步说明。经验表明，多数情况下用该策略修正不超过2次就可以获得满意的结果，解的质量令人满意。

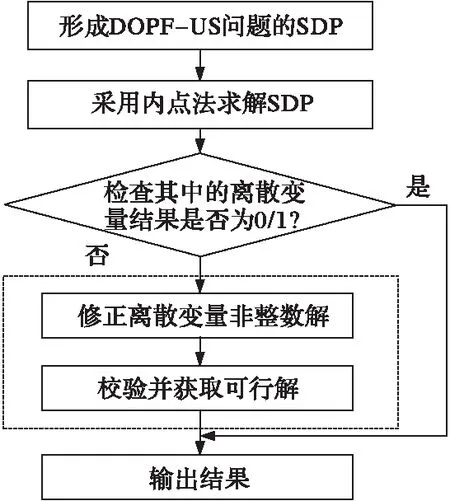
图1 内点半定规划法求解DOPF-UC问题流程

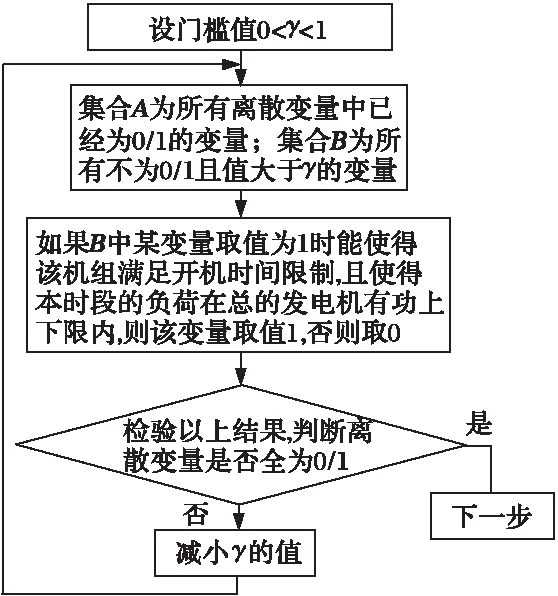
图2 内点半定规划法离散变量处理策略

4 仿真计算及算例分析

本研究对4个规模从6到118的系统进行仿真计算和研究，调度时间均为24 h。其中GX-98是广西的一个实际系统，有36台机组和98个节点。各算例规模列于表1。

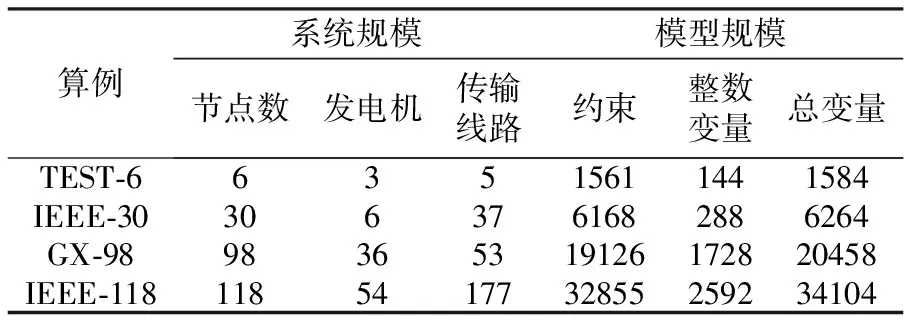
表1 算例规模

4.1TEST-6——六节点系统

本小节用一个6节点的简单电力系统说明SDP求解DOPF-UC问题的结果和优越性，见图3，其中含3台发电机，5条传输线路和2台有载调压器。TEST-6中发电机、节点、有载调压变压器、线路参数及系统24时段负荷分别列于表2至表6。

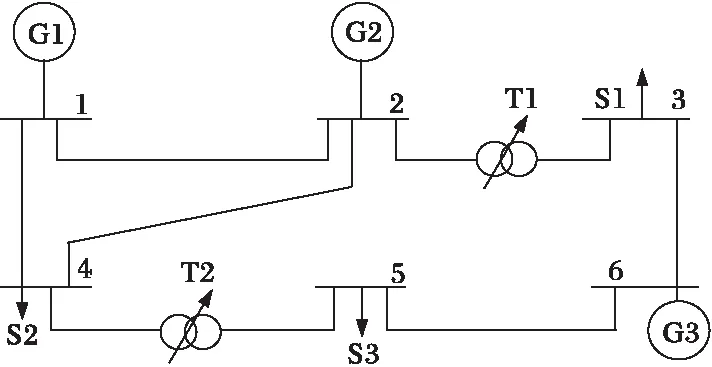
图3 六节点电力系统——TEST-6

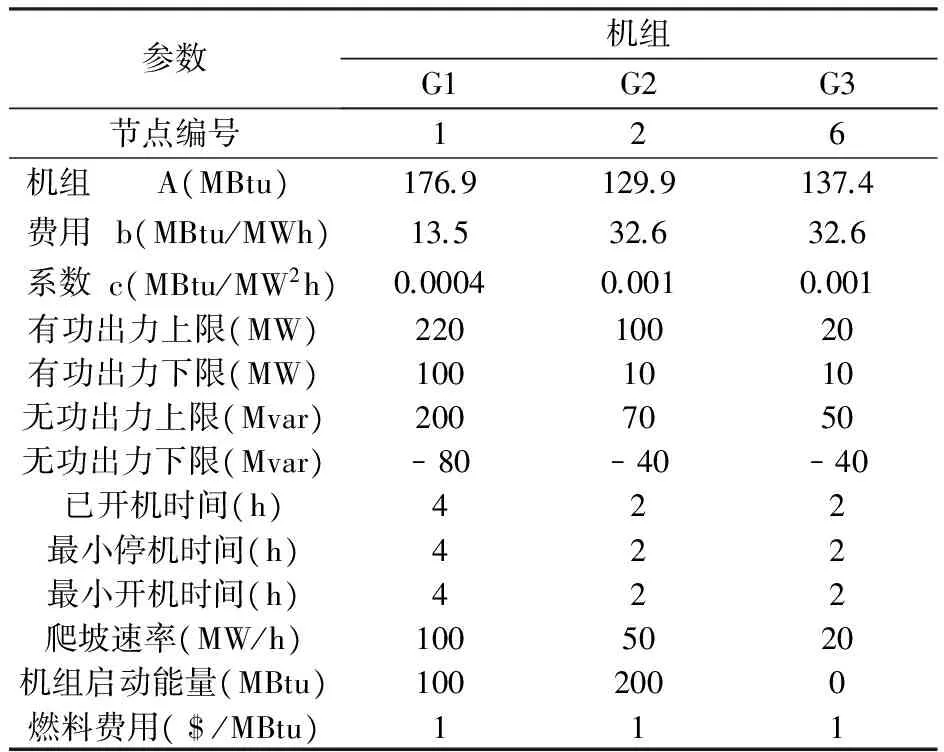
参数机组G1G2G3节点编号126机组A(MBtu)176．9129．9137．4费用b(MBtu/MWh)13．532．632．6系数c(MBtu/MW2h)0．00040．0010．001有功出力上限(MW)22010020有功出力下限(MW)1001010无功出力上限(Mvar)2007050无功出力下限(Mvar)-80-40-40已开机时间(h)422最小停机时间(h)422最小开机时间(h)422爬坡速率(MW/h)1005020机组启动能量(MBtu)1002000燃料费用(＄/MBtu)111

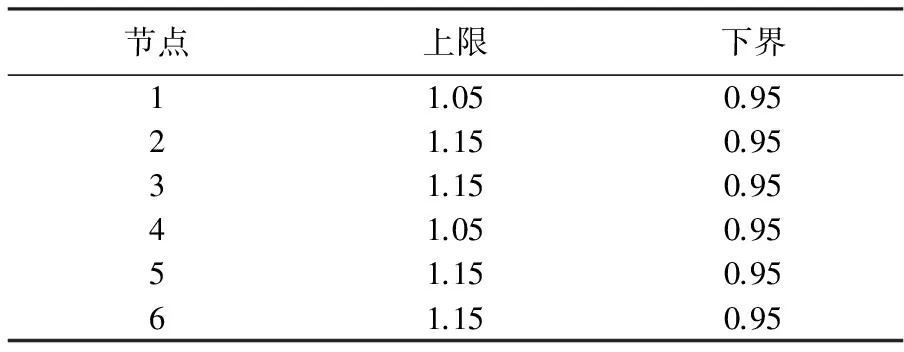
表3 节点电压幅值数据(标幺值)

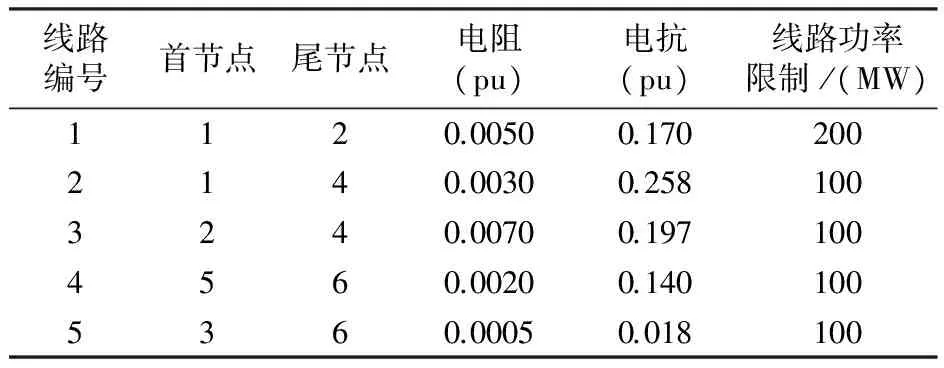
表4 传输线路数据

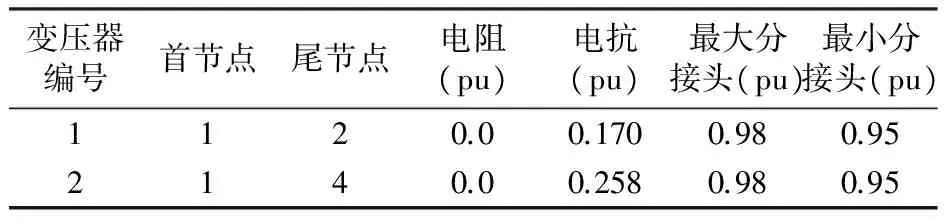
表5 有载调压变压器数据

为详细说明所提方法的有效性，考虑以下2种情况：

1)UC-TEST-6：无任何网络约束，相当于传统的机组组合问题；

2)DOPF-TEST-6：考虑潮流方程、线路传输限制和节点电压限制，为考虑机组组合的动态最优潮流问题。以下分别予以说明。

表6 每小时负荷

4.1.1 UC-TEST-6

运用内点半定规划法求解机组组合问题[21]，机组启停计划列于表7。其中0/1分别表示机组的启停状态。24 h运行费用为$84317.80。可看出，在满足有功功率与负荷平衡的情况下，为使运行费用最小，费用较高的机组2和3在某些时段不开机。

考察该机组运行计划，在时段10中仅有机组1和2投入运行。检查该时段的潮流分布情况，此时线路1-4的有功传输功率为102.38MW，存在线路传输功率越限；同时，节点2和4的电压幅值分别为0.9464和0.9363，低于电压幅值要求。很明显，该机组运行计划不满足实际运行要求。

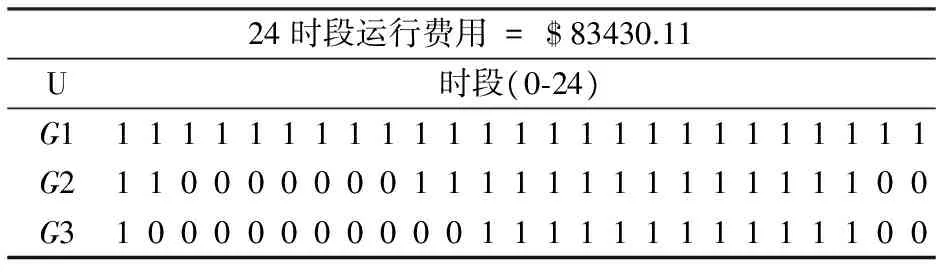
表7 机组启停计划(算例1)

4.1.2 DOPF-TEST-6

用本文所提方法求解计及电网静态安全约束的机组组合问题，机组启停计划列于表8。

表8 计及电网静态安全约束的机组启停计划

按以上计划运行，UC-TEST-6中出现的线路传输功率越限和节点电压越限问题同时被消除。由于考虑了系统网损，且在第10时段为解决越限问题，3台发电机此刻同时投入运行，造成总的运行费用比UC-TEST-6高，达$84317.90。

表9对UC-TEST-6和DOPF-TEST-6计算出的各时段发电机有功出力进行比较。结果表明，由于DOPF-TEST-6考虑了网络约束，机组有功出力和运行费用均有所增加。同时，也正是由于同时考虑了系统安全运行约束，DOPF-TEST-6计算得出的机组运行计划能满足实际运行需要。

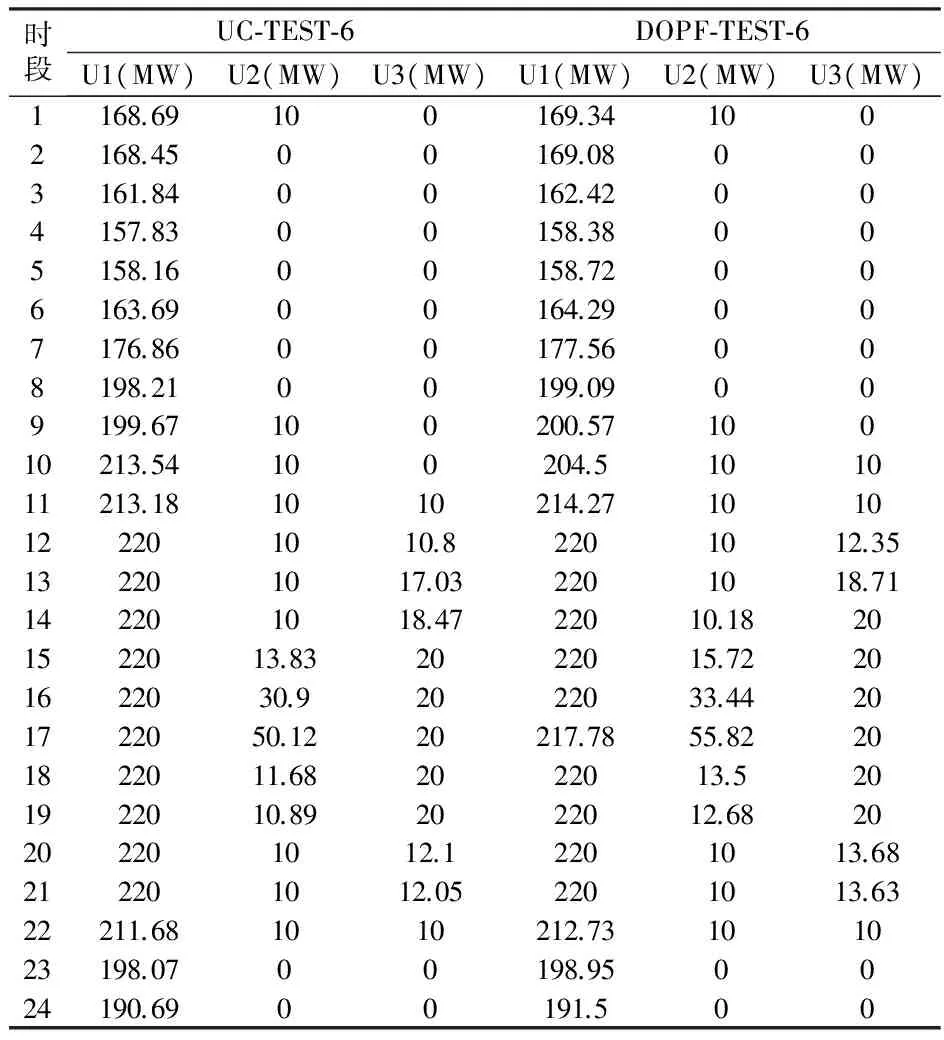
表9 机组调度有功出力比较

4.2 算法性能及其收敛性

采用内点半定规划法能有效地求解DOPF-UC问题。针对少数离散变量的微小偏差采取修正策略，能获得满意的整数解。表10 显示了四个算例中关于离散变量处理的计算情况，其中离散变量值大于0.9的认定为1，小于0.05 的认定为0。门槛值γ从0.5递减。从表中可以看出，随着系统规模的增加，离散变量解的质量也随着提高，用于修正非整数解的计算代价因此降低。

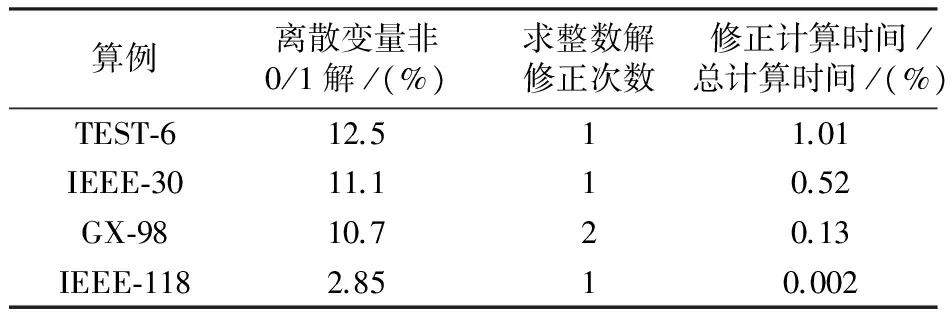
表10 离散变量处理

互补间隙是判断是否达到最优解的一个重要标准，它的变化趋势能反映算法特点。一般来说，判断一个算法优秀与否的标准是其互补间隙能否快速单调递减至0。图4表明，内点半定规划法求解DOPF-UC问题核心计算的互补间隙在给定误差范围内均能于有限次迭代步快速单调收敛趋于0。

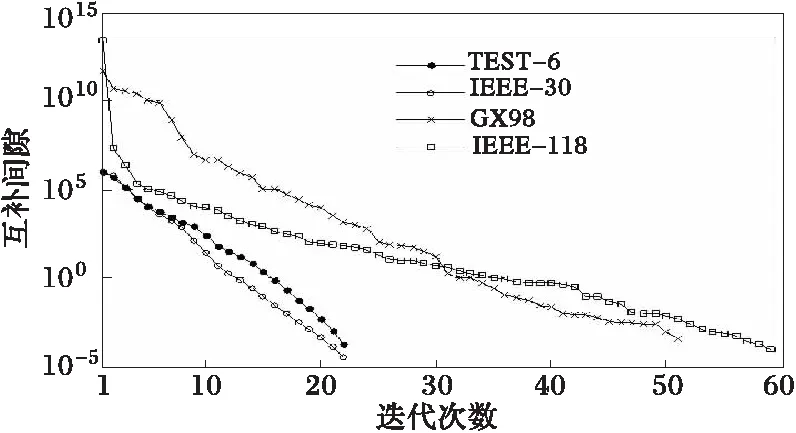
图4 互补间隙收敛曲线

5 结语

本文提出了一种基于内点半定规划模型求解考虑机组组合的动态最优潮流问题的新方法，并系统讨论了如何建立其半定规划模型、相关核心算法步骤和算例仿真分析。仿真结果表明，所提方法能有效处理离散变量，不必对原问题模型分层求解，且算法性能稳定，研究和应用前景广阔。但该方法目前还无法计算超大规模的系统，因此，深入研究相关稀疏技术和并行计算将是以后研究的重点。实际上，这正是数值最优化领域当前的研究热点。

[1] 袁贵川，王建全(Yuan Guichuan, Wang Jianquan).考虑了动态约束和稳定约束的最优潮流(Optimal power flow considering dynamic and stability constraints)[J]. 电力系统及其自动化学报(Proceedings of the CSU-EPSA), 2003, 15(3): 1-5,9,16.

[2] Yamin H Y, Al-Tallaq Kamel, Shahidehpour S M. New approach for dynamic optimal power flow using Benders decomposition in a deregulated power market[J]. Electric Power Systems Research, 2003 , 65(2): 101-107.

[3] Yong Fu, Shahidehpour S M, Li Zuyi. AC contingency dispatch based on security-constrained unit commitment[J]. IEEE Trans on Power Systems, 2006,21(2): 897 - 908.

[4] Abdul-Rahman K H, Shahidehpour S M, Aganagic M,etal. Practical resource scheduling with OPF constraints[J]. IEEE Trans on Power Systems, 1996,11(1): 254-259.

[5] 丁晓莺,王锡凡,张显，等(Ding Xiaoying, Wang Xifan, Zhang Xian,etal). 基于内点割平面法的混合整数最优潮流算法(Mixed integer optimal power flow based on interior point cutting plane method)[J]. 中国电机工程学报(Proceedings of the CSEE), 2004, 24(2): 1-7.

[6] Raglend I Jacob, Padhy Narayana P. Solutions to practical unit commitment problems with operational, power flow and environmental constraints[C]// IEEE Power Engineering Society General Meeting, Montreal, Canada: 2006.

[7] Ragupathi Rajkumar, Das Tapas K. A stochastic game approach for modeling wholesale energy bidding in deregulated power markets[J]. IEEE Trans on Power Apparatus and Systems, 2004,19(2): 849-856.

[8] Adler I, Alizadeh F. Primal-dual interior point algorithms for convex quadratically constrained and semidefinite optimization problems[R]. New Brunswick: Rutgers University, 1995.

[9] Todd M J. Semidefinite optimization[J]. Acta Numerica, 2001,10(1): 515-560.

[10]Wolkowicz H. Handbook of Applied Optimization[M]. New York: Oxford University Press, 2001.

[11]Parrilo P. Structured Semidefinite Programs and Semialgebraic Geometry Methods in Robustness and Optimization[D]. Pasadena : Control and Dynamical Systems, California Institute of Technology, 2000.

[12]Parrilo P A. Sanjay Lall Semidefinite programming relaxations and algebraic optimization in control[J]. European Journal of Control,2003, 9(2-3):307-321.

[13]Alkire B, Vandenberghe L. Convex optimization problems involving finite autocorrelation sequences[R]. Los Angeles: , Electrical Engineering Department of University of Califonia Los Angeles, 2001.

[14]Xiao L, Boyd S. Fast linear iterations for distributed averaging[R]. USA: Stanford University, 2003.

[15]Goemans M X, Rendl F. Semidefinite programming in combinatorial optimization[J]. Mathematical Programming, 1997,79(1):143-161.

[16]Benson Steven J, Ye Yinyu, Zhang Xiong. Solving large-scale sparse semidefinite programs for combinatorial optimization[J]. SIAM Journal on Optimization, 1998,10(1):1-20.

[17]Fujisawa K, Fukuda M, Kojima M,etal. Numerical evaluation of SDPA [R] . Tokyo,Japan: Department of Mathematical and Computing Sciences of Tokyo Institute of Technology, 1998.

[18]Fuentes-Loyola Rodrigo, Quintana Victor H. Medium-term hydrothermal coordination by semidefinite programming[J]. IEEE Trans on Power Systems,2003, 18(4):1515-1522.

[19]Madrigal M, Quintana V H. Semidefinite programming relaxations for {0,l} -Power dispatch problems[C]∥IEEE PES Summer Meeting, Edmonton , Canada: 1999.

[20]白晓清，韦化，Katsuki Fujisaw (Bai Xiaoqing, Wei Hua, Katsuki Fujisaw). 求解最优潮流问题的内点半定规划法(Solution of optimal power flow problems by semi-definite programming)[J].中国电机工程学报(Proceedings of the CSEE)，2008, 28(19): 56-64.

[21]韦化，吴阿琴，白晓清(Wei Hua, Wu Aqin, Bai Xiaoqing). 一种求解机组组合问题的内点半定规划方法(An interior point semidefinite programming for unit commitment problems)[J].中国电机工程学报(Proceedings of the CSEE)，2008, 28(1): 35-40.

[22]Fujisawa Katsuki, Kojima Masakazu, Nakata Kazuhide. Exploiting sparsity in primal-dual interior-point methods for semidefinite programming[J]. Mathematical Programming, 1997, 79(1-3):235-253.

SDP-basedMethodforDynamicOptimalPowerFlowwithUnitCommitment

BAI Xiao-qing， WEI Hua

(College of Electric Engineering, Guangxi University, Nanning 530004, China)

Considering the economy and security of the operation of power system,a semidefinte programming(SDP) model for dynamic optimal power flow(DOPF) problem with unit commitment(UC),named as DOPF-UC,is set up in this paper,which is directly solved by the interior-point method(IPM) on the base of the SDP.The proposed method is applied for the DOPF-UC problems due to its excellent convergence and the ability in handling the discrete variables by a modification strategy and no requirement of the model decomposition,which can be finished within polynomial time.In order to increase the calculation speed,the sparse technology of block matrix operation of SDP is adopted.Four different size test cases from 6 to 118 buses over 24 hours are used to simulate,and the result verifies the accuracy,effectiveness and superiority of the proposed method.Therefore,the research and application of the SDP-based method for DOPF-UC has a good prospect.

dynamic optimal power flow； semidefinite programming； unit commitment； interior point method

2010-01-21；

2010-06-17

TM71

A

1003-8930(2011)06-0067-09

白晓清(1969-)，女，博士研究生，副教授，研究方向为电力系统最优化。Email:baixq@gxu.edu.cn 韦 化(1954-)，男，博士，教授，博士生导师，研究方向为最优化理论及其在电力系统中的应用。