第一性原理研究空位点缺陷对高压下LiF的电子结构和光学性质的影响*

何 旭 何 林 唐明杰 徐 明

(四川师范大学物理与电子工程学院，成都 610068)

(2010年3月10日收到;2010年6月10日收到修改稿)

第一性原理研究空位点缺陷对高压下LiF的电子结构和光学性质的影响*

何 旭 何 林†唐明杰 徐 明

(四川师范大学物理与电子工程学院，成都 610068)

(2010年3月10日收到;2010年6月10日收到修改稿)

基于密度泛函理论框架下的平面波超软赝势方法，分别计算了102 GPa压力下LiF理想晶体、含Li－1空位和F+1空位点缺陷晶体时的电子结构和光学性质.结果表明:空位点缺陷的存在使得LiF能隙中出现了缺陷态;在可见光范围内，空位点缺陷的存在不会影响LiF的高压光吸收性(吸收系数仍为零);在紫外光波段，Li－1空位存在时在约99—114 nm波段内出现了弱的吸收，F+1空位存在时在约99—262 nm波段内出现了明显的吸收;Li－1，F+1两种空位分别存在时对LiF的反射谱和能量损失谱产生的影响都集中在紫外光区，与对光吸收产生的影响相似.

LiF，第一性原理，空位点缺陷，光学透明性

PACS:61.66.－ f，65.40.gk，71.15.－ m，73.20.At

1.引 言

冲击压缩下材料的光谱和温度等测量中需要用到光学窗口材料［1］.因此，冲击压缩下窗口材料在可见光区的透明性问题是人们特别关注的，因为它将对冲击波实验结果的置信度有重要影响［2］.LiF和Al2O3晶体在冲击波实验中常被用作光学窗口材料.因此，研究它们在冲击压缩下光学透明性是否保持的问题对发展冲击波实验的测量技术有重要应用前景［2］.目前，LiF单晶材料在160 GPa的冲击压力范围内具有良好的高压透明性已得到公认［3—5］，并在一些材料的冲击温度测量中获得成功应用［6—8］.但是，实验研究却表明 Al2O3晶体在 100 GPa以上会出现透明性丧失的问题［9］.最近，基于理论计算结果所提出的一个观点认为，该现象与蓝宝石Al2O3晶体在冲击过程中其内部出现的点缺陷有关［10］.通常，在被冲击的固体材料内部将会出现高浓度的点缺陷［11］.但奇怪的是，冲击诱导的点缺陷对Al2O3晶体的高压光学透明性产生影响却没有导致LiF晶体的高压透明性降低，这是一个值得研究的科学问题，这对评价文献［10］中提出的用空位点缺陷的物理机理来解释蓝宝石在强冲击压缩下的光学透明性丧失现象是否合理有重要作用.

目前，采用第一性原理计算方法，人们已研究了LiF理想晶体在高压下的电子结构、光学和热力学性质以及相变行为［12，13］.结果表明，在 500 GPa 的压力范围内单晶LiF具有良好的透明性，并预测在450 GPa附近存在一个结构相变.但尚未探索点缺陷对LiF的高压电子结构和光学性质的影响.本文考虑到需要与文献［2］中的实验结果对比分析，基于第一性原理方法分别计算在102 GPa的压力下LiF理想晶体、含Li－1空位点缺陷晶体以及含 F+1空位点缺陷晶体的电子结构和光学性质，研究点缺陷对LiF在高压下的电子结构和光学性质的影响.

2.理论模型与计算方法

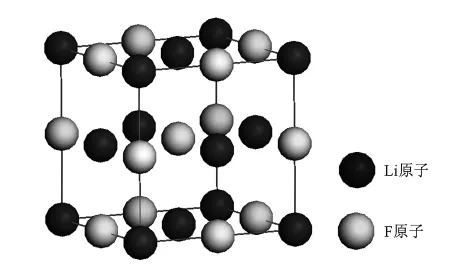
LiF是立方体的 NaCl型结构.图1给出了 LiF晶体的原胞模型.本文在计算理想和含空位LiF晶体的电子结构和光学性质时所用的超原胞模型(含32个原子)都是在该原胞的基础上进行扩展得到的.计算是在 Materials Studio4.3 下的 CASTEP［14，15］中完成的，采用平面波赝势［16］结合局域梯度近似(LDA)的密度泛函理论方法来计算单晶氟化锂(LiF)的电子结构和光学性质.交换相函数是(LDA-CA-PZ)［17］，电子和离子间的相互作用采用超软赝势，几何优化法采用了BFGS［18］算法.优化计算的精确度由下面的条件控制:自洽收敛精度为每个原子2×10－5eV，最大位移偏差为0.002(1=0.1 nm)，K点设置为3×3×6.计算能带结构时平面波截断能设置为300 eV;原子间的相互作用收敛精度为 0.05 eV/，最大应力偏差是0.05 GPa，空带选取为48.对于分别含Li－1和F+1空位的缺陷晶体模型的设置方法是在理想晶体模型靠中间位置分别去掉一个Li或F原子，然后加上不同的电荷，计算方法的设置和理想晶体的相同.

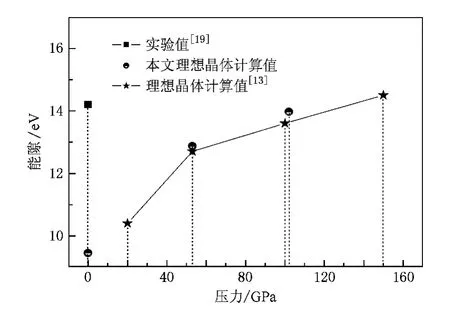
为了说明计算结果的合理性，我们做了如下分析(见图2).1)文献［13］中计算得到了理想LiF晶体的能隙随压力的变化曲线，从该曲线目视外推到零压下的能隙值略低于本文的计算值;而零压下LiF的实验能隙值［19］(14.2 eV)却高于本文的计算值(9.52 eV).应该说明的是，这个明显的差别通常是由第一性原理计算理论的局限性造成的，该理论更适合于预测基态的物性.众所周知，用第一性原理计算半导体和绝缘体材料的电子能隙时常常会导致低估结果，这种偏低可以视为一种系统误差［20］.2)虽然本文计算得到的 LiF理想晶体的能隙随压力变化曲线整体上略高于文献［13］中计算得到的能隙随压力变化曲线，但这两条曲线随压力变化的趋势是一致的.而且，零压下本文计算的数值与实验值更接近.通过以上分析可以认为本文给出的能隙随压力变化关系应该是合理的.

3.计算结果与讨论

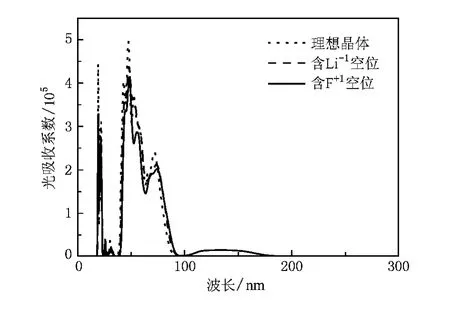
图3给出了102 GPa压力下LiF理想晶体和两种空位(Li－1，F+1)分别存在时的光吸收曲线.由图3可知，在小于100 nm的范围内，两种空位存在下的光吸收曲线与理想晶体的吸收曲线基本相似，只是吸收峰值有所减小.与理想晶体的计算结果相比较，当Li－1空位存在时，在大约99—114 nm的范围内有微弱的光吸收;F+1存在时，在约99—262 nm的范围内有明显的吸收.但在可见光范围内，Li－1和F+1两种空位的存在没有影响LiF的高压光吸收性(吸收系数仍为零).该结果与冲击实验观测到的现象［2］是一致的.需要说明的是，本文用第一性原理方法计算得到的能隙值低于实验值(见图3).因此，如果对计算能隙数据实施修正，会导致计算得到的吸收边出现明显的蓝移.在零压下，计算得到的LiF能隙值比实验值要小约4.3 eV.虽然到目前为止还不能获得LiF在高压下的实验能隙数据，但是基于系统误差的观点［20］，可以认为在102 GPa处仍可能存在4.3 eV的低估.相反，由于第一性原理计算的能隙将随冲击温度(冲击压力为102 GPa时，冲击温度为 2547 K［2］)的出现而降低［20，21］.所以，冲击诱导的热效应将使得计算得到的吸收边发生一定的红移.到目前为止，2547 K的温度会导致LiF高压能隙降低多少仍不清楚，但如果按照文献［10］中的分析来看，2547 K的温度所导致的能隙减小值不足以抵消计算误差修正造成的能隙增加值.所以，在可见光波段LiF的计算数据与其冲击实验观测结果对比是可行的.

为了从微观上解释LiF的高压光吸收特性，我们计算了102 GPa压力下LiF理想晶体以及分别含两种空位(Li－1，F+1)晶体的能带结构和总态密度(见图4和图5).由图4(b)可见，当有 Li－1空位存在时，能隙值为12.43 eV，比理想晶体的能隙值(Eg=13.97 eV)减小1.54 eV且在费米能级附近有缺陷能级出现;图4(c)给出了当F+1存在时的能带结构，由该图可以看出，在费米能级上约6.49 eV处有缺陷能级出现，在图5给出的态密度图中也可以明显看出在LiF的能隙中有缺陷态出现.尽管如此，与文献［10］中 Al2O3的计算结果不同的是:LiF的禁带宽度足够大，缺陷态的出现仍不能使LiF在可见光区出现吸收.这也就解释了冲击诱导的点缺陷为什么会对Al2O3晶体的高压光学透明性产生影响而没有导致LiF晶体的高压透明性降低.由于在可见光区LiF和Al2O［10］3的计算结果都与实验观测现象一致，所以，我们认为从空位点缺陷的角度来分析冲击压缩下蓝宝石的光学透明性丧失现象是合理的.

图4 102 GPa下 LiF的能带结构 (a)理想晶体，(b)含 Li－1空位，(c)含 F+1空位

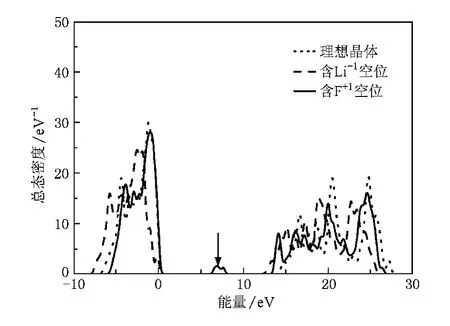
图5 102 GPa下LiF在三种情况下的总态密度

为了直观地理解原子间的成键和作用特性，我们对LiF晶胞中的差分电荷密度进行了分析.图6给出了102 GPa下LiF超晶胞理想晶体及两种空位分别存在下的电荷密度分布情况，三个图中电荷密度分布图均沿 LiF(NaCl型结构下)的100面.由图6(a)可以看出，Li原子与 F原子之间的电子云密度重叠较弱，这表明 LiF晶体中Li—F之间形成的主要是离子键.图6(b)和(c)与图6(a)比较，分别是中心偏左少了一个 Li原子及中间位置少了一个F原子，而且图中可以看出，Li空位或F空位的存在所影响的都是与之相邻的原子差分电荷密度分布，而对次紧邻或更远原子的几乎没有影响.

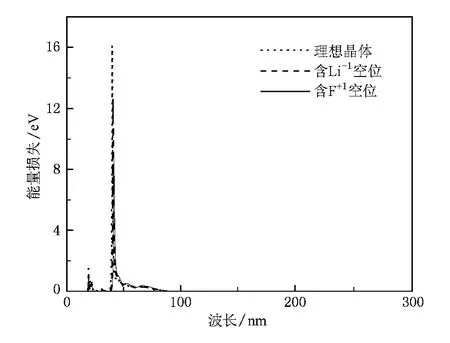
另外，本文还计算了102 GPa压力下 LiF理想晶体及分别含 Li－1和F+1两种空位点缺陷晶体的反射谱及能量损失谱.图7给出了计算得到的随波长变化的LiF反射谱，从该图可以看出，在大约18，39和73 nm处出现了一系列的反射主峰，另外还出现了一系列弱的反射峰.Li－1和 F+1两种空位分别存在时，与理想晶体的反射峰基本上在同一波长处，但各反射峰的强度降低.图8给出了理论计算得到的LiF在三种情况下的能量损失谱.由该图可知，三种情况下LiF的能量损失谱峰大约都位于波长39 nm处，但两种点空位缺陷存在时，在约128—190 nm的范围内出现了一定的影响.结果表明，反射谱和能量损失谱的峰值都存在于紫外光区，与空位缺陷对光吸收性质的影响相似.

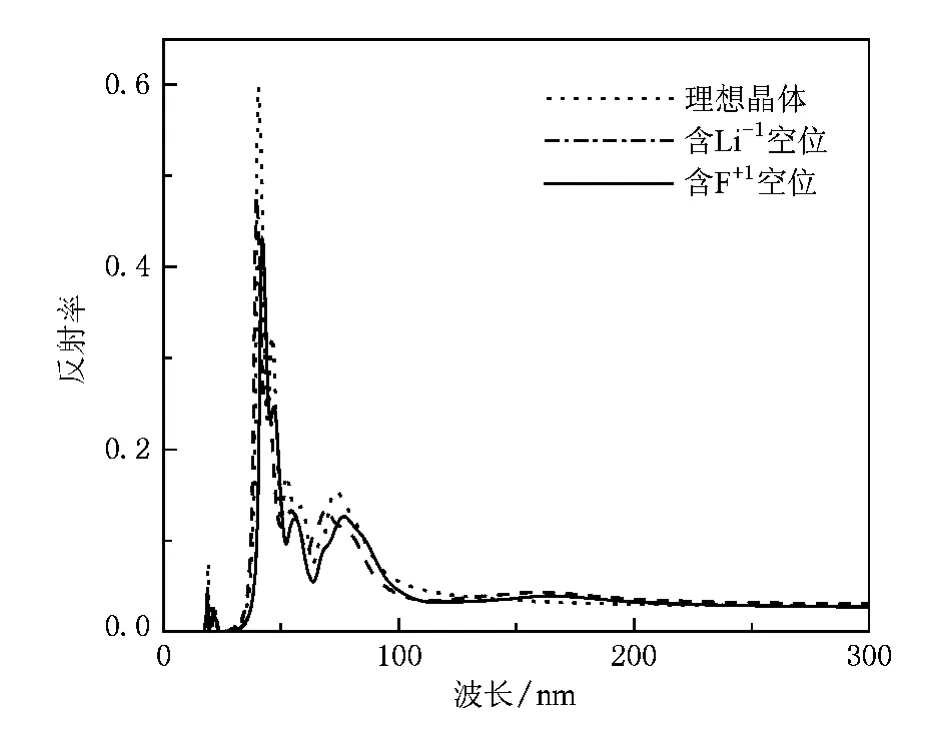
图7 102 GPa压力下LiF的反射谱

4.结 论

基于密度泛函理论框架下的第一性原理方法，本文计算了102 GPa压力下的LiF理想晶体及分别含Li－1，F+1两种空位晶体的电子结构和光学性质.结果表明，Li－1和F+1两种空位的存在使 LiF的能隙中都出现了缺陷能级，从而使得LiF分别在99—114 nm和99—262 nm出现了不同程度的光吸收，但在可见光范围内并没有引起光吸收，与冲击压缩下观察到的实验现象相符合.该结果不仅解释了为什么冲击诱导的点缺陷对Al2O3晶体的高压光学透明性产生影响而没有导致LiF晶体的高压透明性降低的原因，而且也支持从空位点缺陷的角度来解释冲击压缩下蓝宝石的光学透明性丧失现象的观点.另外，本文还计算了102 GPa压力下两种空位分别存在时LiF的反射谱及能量损失谱.数据分析表明，两种空位的存在只对LiF紫外光波段的这些性质产生影响，该结果为高压实验提供了理论参考.

［1］Li J，Zhou X M，Li J B 2008Rev.Sci.Instrum.79 123107

［2］Zhou X M，Wang X S，Li S N，Li J，Li J B，Jing F Q 2007Acta Phys.Sin.56 4965(in Chinese)［周显明、汪小松、李赛男、李 俊、李加波、经福谦2007物理学报56 4965］

［3］Wise J L，Chhabildas L C 1986Shock Compression of Condensed Matter(New York:Elsevier Science Pubilshers)p441

［4］Hicks D G，Celliers P M，Collins G W，Eggert J H，Noon S J 2003Phys.Rev.Lett.91 0355021

［5］Beobler R，Ross M，Boereker D B 1997Phys.Rev.Lett.78 4589

［6］Tan H，Ahren T J 1990High Press.Res.2 159

［7］Bess J D，Ahrens T J，Abolson J R，Tan H 1990J.Geophys.Res.95 21767

［8］Hereil P L，Mabire C 2002Shock Compression of Condensed Matter(New York:Elsevier Science Pubilslhers)p1235

［9］Urtiew P A 1974J.Appl.Phys.45 3490

［10］He L，Tang M J，Fang Y，Jing F Q 2008Europhys.Lett.83 39001

［11］Meyers M A 1994Dynamic Behavior of Materials(New York:Wiley)pp413—420

［12］Shi H F，Dai X F，Ji G F，Liu H，Gong Z Z，Guo Y X 2006J.Atom.Mol.Phys.23 262(in Chinese)［史海峰、代雪峰、姬广富、刘 红、龚自正、郭永新2006原子与分子物理学报23 262］

［13］Li H M，Wu X，Li J，Chen D L，Chu W S，Wu Z Y 2007Acta Phys.Sin.56 7201(in Chinese)［李海铭、巫 翔、李 炯、陈栋梁、储旺盛、吴自玉2007物理学报56 7201］

［14］Segall M D，Lindan P L D，Probert M J，Pickard C J，Hasnip P J，Clark S J，Payne M C 2002Phys.Condens.Matter14 2717

［15］Payne M C，Teter M P，Allan D C，Arias T A，Joannopoulos J D 1992Rev.Mod.Phys.64 1045

［16］Perdew J P，Zunger A 1981Phys.Rev.B 23 5048

［17］Kohn W，Sham L 1965Phys.Rev.A 140 1133

［18］Fischer T H，Almlof J 1992Phys.Chem.96 9768

［19］Piacentini M 1975Solid State Commun.17 697

［20］Holm B，Ahuja R，Yourdshahyan Y，Johansson B 1999Phys.Rev.B 59 12777

［21］Wu J，Walukiewicz W，Shan W，Yu K M，Ager J A III，Li Sx，Haller E E，Lu H，Schaff W J 2003J.Appl.Phys.94 4457

PACS:61.66.－ f，65.40.gk，71.15.－ m，73.20.At

Effects of the vacancy point-defect on electronic structure and optical properties of LiF under high pressure:A first principles investigation*

He Xu He Lin†Tang Ming-Jie Xu Ming
(College of Physics and Electronic Engineering，Sichuan Normal University，Chengdu 610068，China)
(Received 10 March 2010;revised manuscript received 10 June 2010)

By using the ultra-soft pseudo-potential approach of the plane wave based on the density-functional theory，the electronic structures and optical properties of LiF with Li－1and F+1vacancies are calculated.The results indicate that:(1)the presence of the vacancy causes defective states within the band gap of LiF;(2)the optical absorption of LiF in the visible-light region is not influenced by the vacancy point-defect(absorption coefficients are still zero);(3)in the ultra-violet region，the weak absorption induced by the Li－1vacancy，appears within ～ 99—114 nm，and the relatively strong absorption induced by the F+1vacancy exists in the range of 99—262 nm;(4)effects of the Li－1and F+1vacancy on reflectivity and loss-function show mainly in the ultra-violet region，which is similar to those of optical absorption.

LiF，first principles，vacancy point-defect，optical transparency

*国家自然科学基金(批准号:10299040)和四川师范大学科技基金资助的课题.

†通讯联系人.E-mail:linhe63@yahoo.com.cn

*Project supported by the National Natural Science Foundation of China(Grant No.10299040)and the Science and Technology Foundation of Sichuan Normal University，China.

†Corresponding author.E-mail:linhe63@yahoo.com.cn