无线传感网络中基于共面度的三维定位算法研究与设计*

毛科技，赵小敏，邵 奔，陈庆章

(浙江工业大学计算机科学与技术学院，杭州 310023)

无线传感网络节点定位，简单的说就是节点通过某种方法或者执行某种算法获得自己在网络中的位置，通常以坐标的形式表示，也可以用大致的位置(如房号)等表示［1］。由于全球定位系统(GPS)技术成熟，获得节点的位置可以通过给节点安装GPS接收器直接获得，但受其价格、体积、功耗、信号屏蔽等诸多因素制约，所以通过GPS获得所有节点的位置存在一定的困难。目前大多数的定位技术都是利用网络中少量已知位置的节点通过定位算法获得其它未知节点的位置，已知位置的节点称为参考点，可以人为放置或者通过GPS获得。未知节点的位置可以是相对于参考点建立的坐标系，也可以是一个绝对位置(如参考点采用 GPS 定位)［2－3］。

由于无线传感网络节点分布的随机性和节点感知信息的位置依赖性，节点准确地进行自身定位是无线传感网络应用的重要条件。

1 研究背景

由于无线传感网络对节点的能耗、成本、体积等要求，所以定位算法必须在满足上述要求的前提下才有实际的使用价值。目前，科研工作者已经研究出了多种定位算法，如 SpotON［4］，APS［5］，MDS-MAP［6］等。另外，无线传感网络的定位算法分类方法众多，较为典型有基于测距(Rang-based)和距离无关(Rangfree)的分类方法。其中基于测距的定位算法常用的测距技术有 RSSI，TOA，TDOA，AOA［7］等。大部分的测距算法都靠额外设备来提高定位精度，如使用RFID技术、超宽带(UWB)技术、超声波技术和使用天线阵列进行基于角度的定位等［8－10］。距离无关的定位算法则是利用网络的连通性或者跳数对未知节点的位置进行估计。由于测距技术在功耗、成本等方面有较高的要求，所以在距离无关算法上的研究是非常具有意义的，目前众多的距离无关算法中DV-Hop算法是最为典型并且备受关乎的。DV-Hop算法思想简单，容易实现，但是由于其定位精度较低，受网络拓扑影响较大，且跳数越多误差越大，所以在实际的无线传感网络中应用效果较差。

1.1 三维定位问题

到目前为止，很多学者已经提出了比较典型的面向二维平面的定位算法，然而很少有涉及如何解决三维空间的定位问题。但是实际环境中传感器节点是经常被部署在三维空间中的，比如多楼层的建筑物里，地面起伏不定的山坡上以及水下空间等等。在三维环境下的定位问题相比于二维平面显然会有一定区别，其主要难点如下:

(1)定位所需的参考点增加 在二维平面里，定位一个未知节点只需三个参考节点，而在三维空间里，最少需要四个参考节点才能定位一个未知节点。这带来的不仅是对参考点密度的要求，而且增加了算法复杂度。

(2)地形障碍对传输信号的影响 室外二维环境下，节点的传输信号一般不受地形或者障碍影响，但是三维空间里地形因素带来的非视距传输对信号的影响是不可忽视的，所以使用信号强度等计算节点之间距离的算法就会产生一定误差，使用非测距算法的同时也要考虑节点最小通信半径受影响带来的连通性问题。若不考虑这些因素肯定会对定位精度产生很大影响。

(3)难以满足特定应用场合的需求 对于一些特定应用场合的三维定位，如建筑物中，定位结果必须能够反映出节点所处的楼层。由于楼层之间的距离有限，无法达到厘米级精度的定位算法基本难以确定节点处于哪一楼层，这是室内三维定位目前急需解决的问题。

本研究将DV-Hop思想用于三维定位，其一是将三边定位改为四边定位;其二是解决网络拓扑和参考点分布对定位算法造成的影响，提出一种定位算法的优化方法以提高精度;其三是考虑建筑物中三维定位存在的问题，结合实际应用，提出一种适用于建筑物内的复杂度低的三维定位算法。

2 基于共面度的三维定位算法

在定位过程中，利用多边定位法时至少能确定一个未知节点的参考点组合叫做一个定位单元。在二维平面中，当计算出一个定位单元中每个参考点到未知节点的距离时，就可以利用三边测量法去确定未知节点的位置。但是在计算机未知节点到参考点的距离时，往往存在一定的误差，这使得原本三边定位中的三个圆并不交于一点，所以要用估算的方法去确定未知节点的位置。但是当定位单元中的三个参考点分布在近似于一条直线的情况下时，三个圆的交点有两个，所以不能估计未知节点的位置［11］。同样的问题在三维定位中也存在，在三维空间中，由于测距误差使得定位单元中的四个球面未必存在交点，同样当四点近似共面时，四个球面的交点有两个，从而难以估算未知节点的位置。目前二维定位已有学者提出了共线度的概念［11］，那么为了解决三维定位中的问题，本文引入了共面度的概念，并提出了基于共度面的三维定位算法。

2.1 共面度的定义

共面度即表示三维空间中四个点的共面程度，文献［12］中提出了四面体形状测量被用于评价有限元网格(Finite Element Meshes)中四面体的质量，其中分析和比较了四面体形状的三种不同测量方法:最小立体角(Minimum Solid Angle)，半径比(Radius Ratio)和均值比(Mean Ratio)。下面主要介绍半径比法。

在二维平面中，三角形的内切圆半径和外接圆半径之比的两倍可以表示三角形的半径比，其取值范围为［0，1］，图1表示了二维平面下三角形的半径比。那么扩展到三维空间，四面体T的半径比则定义为ρ=3rin/rcirc，其中rin和rcirc分别为四面体T的内切球半径和外接球半径。

图1 二维平面的三角形半径比

文献［13］中给出了计算四面内切球和外接球半径的公式:

其中v为四面体的体积，si是四面体四个面的面积，a，b，c分别为四面体三组对棱长度的乘积。

任意四面体的体积计算问题可以通过矩阵计算获得。根据四面体半径比的计算公式，结合式(1)和式(2)得到四面体半径比ρ的计算公式为:

其比值范围为(0，1］，当接近0时四面体的四个顶点近似共面，为1时转化为正四面体。

为了简便起见，采用半径比法的共面度如下式表示

其取值范围为［0，1］。

2.2 多重阀值约束策略

在DV-Hop算法的第二阶段，参考点获得与邻近参考点之间的距离和跳数信息后，计算平均每跳距离。由于该算法针对的是多跳网络，在计算平均每跳距离时可能将很远的参考点也包含进来，在对DV-Hop算法进行仿真后发现，若参考点之间的跳数越多，即距离越远，参考点计算的平均每跳距离误差也更大。另外在算法的第三阶段，即定位未知节点的时候，未知节点和定位单元之间的距离越远，共面度约束带来的定位影响越小，且定位误差也越大。所以我们需要对算法引入两个阈值进行约束。

2.2.1 跳数阈值

在大规模无线传感网络中，节点数量多且分布广，跳数阈值(thre_hop)确保了在定位过程中所有传感器节点只与邻近的几个节点交换定位所需信息。采用跳数阈值对节点选择进行约束不但避免了因跳数过多带来的定位误差，而且对于某一未知节点，参与定位的定位单元减少，使得算法复杂度降低，延长了节点的使用寿命。

2.2.2 共面度阈值

共面度阈值(thre_hop)保证了对最佳定位单元的选择，但是设置共面度阈值也存在其优缺点，优点是排除了参考点共面带来的节点不可定位问题并且提高了定位精度，缺点则是造成了总体可定位节点的比例降低，其原因是共面度阈值造成了许多定位单元不能参与定位，对于某些与少数参考点连通的未知节点来说，设置这一约束条件很容易使得该点成为不可定位节点。

总之，多重阈值的约束策略对定位精度的提高和算法复杂度的降低是显而易见的，但是阈值是一个灵活的数字，不能光评理论去讨论阈值的最优解，只有通过模拟和实际应用才能找到权衡各个方面的最佳阈值。

3 算法仿真与分析

在MATLAB6.5下对本文提出的算法进行了仿真，并且比较对象是在三维空间中利用四边定位法的DV-Hop算法，主要的性能指标有算法的定位误差率(Localization Error Ratio，LER)，定义为未知节点定位误差的平均值与节点通信半径的比值;算法的可定位节点比例(Localized Node Proportion，LNP)，定义为定位算法运行结束后能够成功定位的未知节点总数占网络中所有未知节点总数的比例，和不良节点比例(Bad Node Proportion，BNP)，定义为定位误差大于节点通信半径的不良节点数占所有可定位节点的比例。仿真实验还需要配置的一些参数包括节点的数量，节点的通信半径，网络密度(网络平均连通度)，参考点比例等［14，15］。

在仿真实验中，首先需要给定网络环境。本实验将节点所处的网络环境设置在一个100 m×100 m×100 m的三维区域中，参考点和未知节点共100个，且坐标是随机产生的。在测试共面度阈值和跳数阈值变化对定位性能影响的实验中，得出的结论是共面度阈值和跳数阈值的设置对节点的LER和BNP有较为显著的改善。但是在共面度阈值超过0.4以后不管对LER还是BNP的改善都趋于平稳，而对LNP的降低却比较明显，所以将共面度阈值设置在0.4～0.6之间将既能满足较好的定位精度也能实现较好的定位覆盖率，在对原算法的比较实验中本文将共面度阈值设置在0.5。

节点通信半径R根据不同的网络密度设置，参考点比例分别为10%和20%，网络密度从4到14的范围内变化。另外thre_dcp固定为0.5且thre_hop为4。最后的结果经过多次测量取平均的方法来获得。

观察图2(a)，在定位误差率上，当参考点比例相同时，DCP3D的误差相比DV-Hop算法有10%以上的降低，并且当网络密度变化时，前者甚至在参考点比例为10%的情况下超过了后者在参考点比例20%时的定位精度，由此可见DCP3D算法相比DVHop算法在定位精度上有明显的改善。

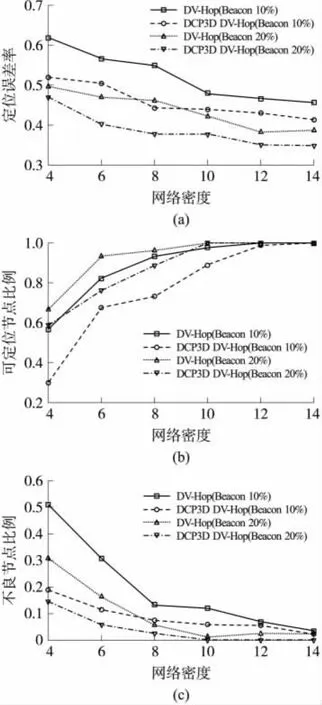
图2 仿真实验结果对比

在可定位节点比例上，图2(b)，DCP3D算法相比DV-Hop算法在网络稀疏的时候降低较为明显，但是当网络密度超过10的时候，DCP3D算法和DV-Hop算法都能够达到90%以上的可定位节点比例。另外，DCP3D算法在参考点比例为20%的情况下，其可定位节点比例已经基本与参考点比例10%情况下的DV-Hop算法持平。由此得出通过适当增加网络密度或者提高参考点比例可以使改进算法在网络覆盖率上表现更好。

在不良节点比例上，图2(c)，无论网络密度与参考点比例多少，DCP3D算法都将其维持在20%以下，并且当网络密度仅仅提高至6的时候，不良节点比例已经减少到10%以下，所以DCP3D算法在改善不良节点方面有卓越的表现。而DV-Hop算法在网络密度和参考点比例低的时候，不良节点比例甚至超过了50%。由此可见，DCP3D算法针对节点密度的变化表现出了更好的稳定性。

总结实验结果，不管在定位精度还是不良节点比例上，DCP3D算法都比DV-Hop算法表现出了更优越的性能，但是唯一不足是可定位节点比例较DV-Hop算法有所降低，这可以通过增加网络密度和参考点比例来改善。由于一般的无线传感网络节点的部署密度不会太低，所以改进算法在实际应用中的定位覆盖率基本能够达到要求。综合各项性能指标，DCP3D算法比DV-Hop算法更适用于无线传感网络三维定位。

4 总结

本文从无线传感网络定位技术存在的问题入手，分析了目前距离无关定位技术的研究现状，针对三维定位技术的不成熟，在距离无关算法中典型的DV-Hop算法基础上，通过引入共面度的概念消除了三维定位中定位单元近似共面对定位结果造成的影响，并且提出了多重阈值约束策略优化算法，提高了定位精度，很大程度上减少了不良节点出现的可能性，具有较好的稳定性。在设置合理的阈值条件下，该算法对可定位节点比例的影响可以忽略，证明了在总体的性能上比DV-Hop算法更为优越。

［1］Ma Zuchang，Sun Yining，Mei Tao.Summary for Wireless Sensor Network［J］.Journal of China Institute of Communications，2004，25(4):114－124.

［2］Hady S A，Stephan O.A 3d-Localization and Terrain Modeling Technique for Wireless Sensor Networks［C］//Proc.of the 2nd ACM Int’l workshop on Foundations of wireless ad hoc and sensor networking and computing.2009，37－46.

［3］李晓维，徐勇军，任丰原.无线传感网络技术［M］.北京理工大学出版社，2007.35.

［4］Hightower J，Boriello G，Want R.SpotON:An Indoor 3D Location Sensing Technology Based on RF Signal Strength［C］//Technical Report UW CSE 2000，Seattle:Department of Computer Science and Engineering.University of Washington，2000.452－463.

［5］Nicolescu D，Nath B.Ad-Hoc Positioning Systems(APS)［C］//Proc.of the 2001 IEEE Global Telecommunications Conf.Vol.5，San Antonio:IEEE Communications Society，2001.2926－2931.

［6］Shang Y，Ruml W，Zhang Y，et al.Localization from Mere Connectivity［C］//Proc.of the 4th ACM Int’l Symposium on Mobile Ad Hoc Networking ＆ Computing.Annapolis:ACM Press，2003.201－212.

［7］Shi Long，Wang Fubao，Duan Weijun.Self-Localization Mechanism and Algorithm for Wireless Sensor Networks［J］.Computer Engineering and Applications，2004，23:127－130.

［8］Oppermann I，Stoica L，Rabbachin A，et al.UWB Wireless Sensor Networks: UWEN—A Practical Example ［J］. IEEE Communications Magazine，2004，42(12):27－32.

［9］Lim H，Kung L，Hou J，et al.Zero-Configuration，Robust Indoor Localization:Theory and Experimentation［C］//Proc.of IEEE INFO-COM 2006.April 2006.30(8):15－19.

［10］Nasipuri A，Li K.A Directionality Based Location Discovery Scheme for Wireless Sensor Networks［C］//Proceedings of the 1st ACM international workshop on Wireless sensor networks and applications.2002，105－111.

［11］Poggi C，Mazzini G.Collinearity for Sensor Network Localization［C］//Proceedings of 2003 IEEE 58th Vehicular Technology Conference.Piscataway，NJ，USA:IEEE，2004.3040－3044.

［12］LIU A，JOE B.Relationship Between Tetrahedron Shape Measures［J］.BIT Numerical Mathematics，Springer Netherlands，1994，34(2):268－287.

［13］Mitrinovic D，SPecaric J E，Volenec V.Recent Advances in Geometric Inequalities［J］.Kluwer Academic Publishers，Dordrecht，The Netherlands，1989.pp.463－555.

［14］王世香.精通MATLAB接口与编程［M］.北京:电子工业出版社，2007.

［15］于斌，孙斌，温暖.NS2与网络模拟［M］.北京:人民邮电出版社，2007.