物流配送线路工作量的衡量方法

谷炜，张超

（北京科技大学经济管理学院，北京100083）

物流配送线路工作量的衡量方法

谷炜，张超

（北京科技大学经济管理学院，北京100083）

文章从内蒙古自治区包头烟草公司的物流配送过程的实证研究角度出发，确定了利用单条配送线路所需的总工作时间来衡量单条配送线路的工作量。根据实际调研所测数据利用数理统计与分析方法，确定了影响单条配送路线总工作时间的具体因素、以及因素对配送过程所需的时间的影响、配送工作时间统计特性、并建立了具体的指标公式来表述单条配送线路工作量大小。

物流配送；线路划分；工作量衡量；实证研究

0 引言

在物流配送中心末端配送集中送货问题求解过程中，需要将大规模复杂不可解的配送网络分解成有限的、小规模、可控可观测的单车配送线路（即配送区域）的问题，并在此基础上针对不同的配送区域，按照每个零售客户订单，相应采取不同的单车线路优化策略。实际上，这是一种“化整为零，各个击破”解决思路。显然，配送线路的划分是一个多约束、多目标决策的组合优化问题，属于NP难问题[1]。

衡量每条线路的工作负荷是配送过程优化的首要任务。如何衡量每条线路工作负荷目前为止学术界还没有定论，多数学者利用行驶距离、送货量等指标赋予不同权重来定义工作量。如文献[2]中定义的广义工作量，认为工作量主要由行驶距离、送货量和零售商网点数量这三个因素决定，对决定不同线路工作量大小的三个参数进行加权求和，对每条线路进行多指标综合评价，并对广义工作量做了如下定义：

衡量一条配送线路工作量负荷大小的指标称为“广义工作量W”[3]，其值为：

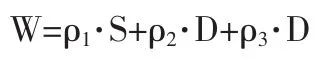
其中，W为广义工作量；S为行驶距离（km）；D为送货量（件）；N为网点数目（个）；ρ1为行驶距离权值（1/km）；ρ2为送货量权值（1/件）；ρ3为网点数权值（1/个）。

上述定义中如何确定3个权重是一个比较困难的问题，因为工作量大小是客观存在的，不能人为判断3个影响工作量的权重是多少。是否这些指标有一个共同的因素来决定工作量的大小，这样工作量大小就可以由这一因素来直接反映。如果找到这个因素就可以避免求权重问题，从而能够更客观、更真实地衡量真实的工作量。经过实地调研发现，在实际配送工作中，工作量大的线路所需要的工作时间就越长，如行驶距离远则花费在路上的时间就越长，而配送点数越多，则服务客户所需的时间也就越多。因此可以试着利用配送工作所需的总时间来衡量配送线路的工作量。

影响配送工作时间的因素有哪些、它们如何影响配送过程所需的时间、配送工作时间具有怎样的统计特性、如何建立具体的指标公式来表述工作量大小是本文研究的主要内容。

1 实证研究对象及问题

1.1 实证研究对象及基础数据

为解决如上问题，我们对内蒙古自治区包头烟草公司的物流配送过程进行了实证研究，选取了包头烟草配送中的42条线路进行了实地跟车体验，记录了整个配送流程。根据调研，包头市共有7500余户烟草零售户，配送中心有配送车辆32辆（城区24辆）、19个访销员、25个客户经理（城区20个，农网5个）。每天分3批次访销约1600户客户。每户每周电话访销、配送一次（6类以上一次，7-9类每周两次）。市区内（不含下属旗县）共有有效用户5182户，电子结算客户4367户，电子结算率为84.27%。

记录数据主要包括每辆车从配送中心出发后的行驶时间、到达网点时的时间和行驶公里数、送货员途经各个网点的滞留时间、不同送货线路的巡回公里数、巡回时间、送货量大小以及每次送货网点数等基础数据等，同时了记录送货过程存在的问题。如表1所示。表2是其中一条线路的详细跟车记录。这些原始数据和存在的问题是本文研究的重要基础。

表1 实地跟车记录表

表2 线路line1 2009年7月28日上午详细跟车情况记录表

1.2 实证研究发现的主要问题

通过实地跟车调研、交流，以及对整个物流配送中心业务流程、数据流程的仔细调查分析，使我们对包头烟草物流送货线路现状和存在问题有了一个较为全面和深刻的认识，归纳起来主要有以下几点：

（1）工作量不均衡，有些线路工作量明显较大。例如调研线路13，巡回里程跑了43.5公里，送了2326条烟，整个配送过程用了3小时15分钟。明显较其它线路工作量大。

（2）装配不考虑实际车容，目前送货车容量偏小，送货效率较低。尤其在月初客户一次订货较多时，一条线路必须多次装、送货才能完成任务。

（3）实际送货时间不长，但由于交通拥堵、红绿灯限制等因素的影响，主要配送时间消耗在了配送过程的往返路上。

（4）存在不同的访销员对应的客户网点在同一个配送区域的情况。

（5）有些客户网点由于道路交通法规限制，送货车辆不能直接开到客户网点处，都是送货员将送货开到一个地方后逐一给客户打电话，由客户自取，一般这些客户自取须走较长距离（如线路1中的“Customer1”、“Customer2”、“Customer3”等客户，整个配送花了近20分钟），严重影响了送货效率。

2 单条配送线路工作量的衡量方法研究

2.1 衡量方法确定

通过调研，我们发现一次完整的配送工作包括两部分，一部分工作是行驶，另一部分工作是服务。而工作量衡量完全可以用工作时间来描述，线路巡回里程长且送货量大的线路配送时间都较长。因此我们把配送过程的总时间划分为两部分，即Ttotal=Tg+Ts。其中Tg为行驶时间，Ts为服务时间，如何利用行驶时间和服务时间的统计量描述区域内总的配送工作所需要的时间是本节要讨论的内容。

2.2 配送服务时间研究

服务时间是指配送车辆到达配送点到该车辆离开配送点的这段时间，配送工作人员在这段时间内主要完成搬运、结算、签字等服务工作。

通过对服务时间的分析我们发现服务时间长短与是否收取现金有关，原因是在收取现金时配送人员需要做核对现金数目等工作，这部分工作占用了服务工作较多的时间。通过研究发现服务时间与送货量的相关性较小，原因是大多配送点的客户都会组织人员搬运自己的货物，所以送货量的增加并没有导致服务时间加长。

利用探索分析检验[4]。对服务时间按是否收现进行分类，而后分别进行分析发现两种情形均服从正态分布。表3是利用SPSS分析得到的结果。

表3 电子结算服务时间统计描述

首先分析电子结算的服务时间：

一般来说，正态检验包括以下步骤[5]：首先生成正态概率图，而后进行假设检验，以检查观测值是否服从正态分布。

对于正态性检验，原假设为：

H0：数据服从正态分布

备择假设为：

H1：数据不服从正态分布

一般来说，正态性检验使用柯尔莫哥洛夫统计量来进行检验[5]。根据格里汶科定理，我们可以把子样经验分布函数看作实际母体分布函数的缩影。如果原假设成立，它与母体分布的差距一般不应太大，由此柯尔莫哥洛夫提出如下统计量：

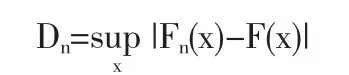
柯尔莫哥洛夫已经证明统计量Dn的精确分布和极限分布K(λ)都不依赖于母体的分布。而且柯尔莫哥洛夫给出了Dn的分布极限分布函数值表及利用Dn得到的柯尔莫哥洛夫检验临界值表。

表4为利用SPSS做的柯尔莫哥洛夫检验，看到统计量为0.101，概率值为0.000。则应该接受原假设，认为电子结算服务时间服从正态分布。

表4 电子结算服务时间正态性检验

Q-Q图检验基本方法[6]是首先将容量为n的样本从小到大排序得到x1≤x2≤…≤xn，则样本的经验分布函数可表示为

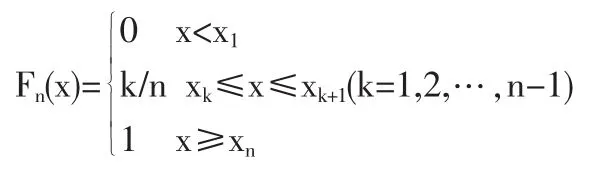
若样本来自正态分布总体，则经验分布函数应近似于正态分布函数，即Fn(x)≈F(x)，u=准-1(Fn(x))，则x≈σu+μ，在x～u平面上是一条直线。当x=xk时,实际上取相应的是N(0,1)的分位点，此时点(xk,uk)应该近似在直线上。如果由样本计算出的n个点近似在直线x≈σu+μ上，则可认为它来自正态分布。

图2是QQ电子结算服务时间Q-Q图，从图2中看出服务时间中存在异常点，经过核实，该点是送货车辆到达配送点时，客户没有在家，送货车辆在该点等了很久，因此导致服务时间异常。异常情况我们予以剔除，剔除异常点的探索分析如下：

通过以上分析看出服务时间服从正态分布，并通过了K-S检验和S-W检验。统计结果表明服务时间期望为1分09秒。我们认为配送过程中每个电子结算的客户的服务时间为1分09秒。

同理分析得到非电子结算的客户服务时间为4分17秒。

利用以上的分析结果我们得到任何一个配送区域内的期望总服务时间为：

Tareas=N1·1.15+N2·4.28

其中N1为该配送区域内电子结算客户数量，N2为该配送区域内非电子结算客户数量。

表5 剔出异常点后电子结算服务时间正态性检验

2.3 配送行驶时间研究

表6为行驶时间和行驶距离的相关关系分析，相关系数取值为[0，1]。一般认为相关关系在0.8以上就是强相关关系，即认为两者存在明显的关系表达式。相关关系在0.3到0.8之间认为是相关关系，相关系数在0.3以下则认为存在弱相关关系。

从表6中可以看出行驶时间和行驶距离的相关关系达到了0.921，呈高度相关。因此可以利用行驶距离对行驶时间做回归分析。

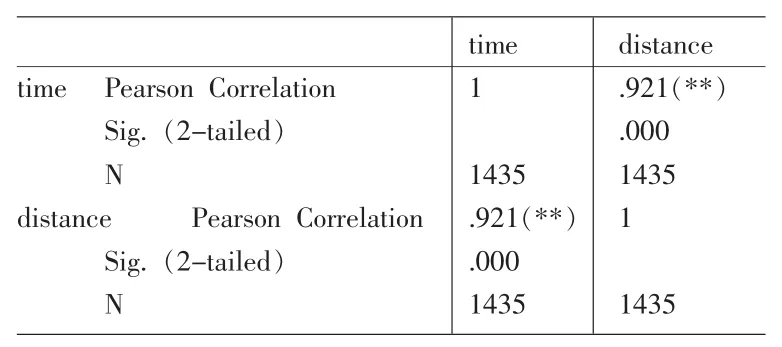
表6 行驶时间和行驶距离相关性分析

通过散点图5可以大概估计出行驶距离和行驶时间存在何种关系。通过图5我们发现行驶距离和行驶时间呈简单线性关系，利用SPSS做回归分析，分析结果如下。

回归方程假设为T=α+βD，其中，T为行驶时间，D为行驶距离，α，β为参数。

表7是回归结果统计，从表中看出复决定系数为0.921，说明回归的效果较好。但回归模型是否真正描述了变量D和T之间的统计规律性，还需要运用统计方法对回归方程进行检验。

表7 回归统计

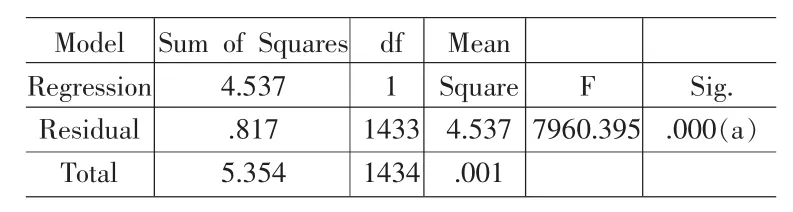
表8 回归方差分析

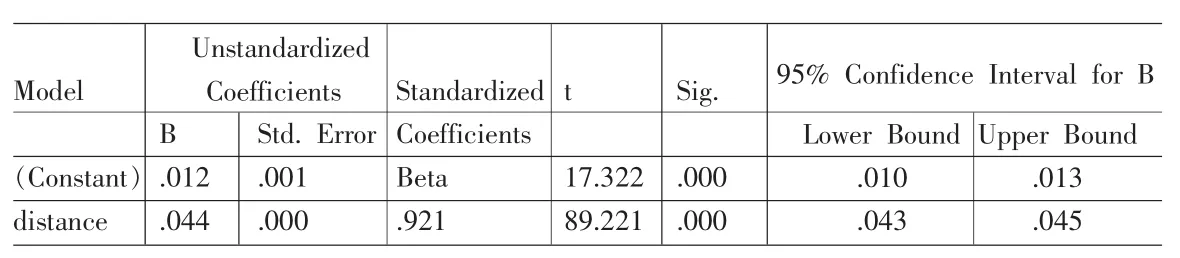
表9 回归系数

通过回归分析得到行驶时间的回归模型为：

T=0.012+0.144×D

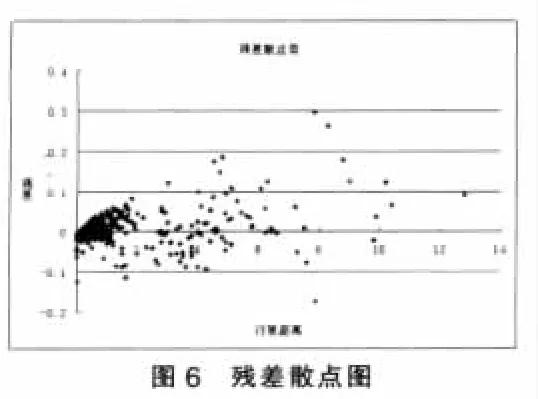
其中D为行驶距离。方差分析表及回归系数表表明该回归模型均通过显著性检验。图6是对回归结果进行的残差检验。

通过图6看出残差随行驶时间增大而增大，具有明显的规律，初步判断模型随机误差项的方差是非齐性的，存在异方差。下边利用斯皮尔曼（Spearman）检验是否存在异方差性。

斯皮尔曼（Spearman）检验又称为等级相关系数法，是一种应用较为广泛的方法。这种检验方法既可用于大样本，也可用于小样本。进行等级相关系数检验通常有三个步骤[4]：

第一步，作y关于x的普通最小二乘回归，求出误差ε的估计值，即残差值e。

第二步，取e得绝对值，即|e|，把x和|e|按递增或递减的次序排列后分成等级，按下式计算出等级相关系数

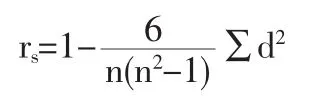
其中，n为样本容量，d为x和|e|的等级的差数。

第三步，做等级相关系数的显著性检验。在n>8的情况下，用下式对样本等级相关系数rs进行t检验。检验统计量为

如果t≤tα/2(n-2)，可以认为异方差问题不存在，如果t>tα/2(n-2)，说明x和|e|之间存在系统关系，异方差问题存在。

对于本问题，利用SPSS检验结果如下：

ABSE为残差的绝对值。通过分析看出残差绝对值与行驶距离的等级相关系数r=0.620，P值为0.000，认为残差绝对值与行驶距离显著相关，存在异方差。

产生异方差的原因很多，需要对问题做认真分析才能找到产生异方差的原因。经过对配送过程的分析，我们发现配送车辆在从配送中心到第一个配送点和由最后一个配送点返回配送中心时，配送司机行驶速度都较快。而配送车辆在由一个配送点到另一配送点时配送司机要随时注意停车，因此行车速度较慢。鉴于以上分析，我们把配送行驶过程分为两类。配送车辆在从配送中心到第一个配送点和由最后一个配送点返回配送中心这两种情况我们定义为全速行驶。配送车辆在由一个配送点到另一配送点的情况我们定义为配送行驶。下面对这两种情况分别进行分析。首先对全速行驶情况进行分析：

通过表10看出回归方程及回归系数均通过显著性检验。

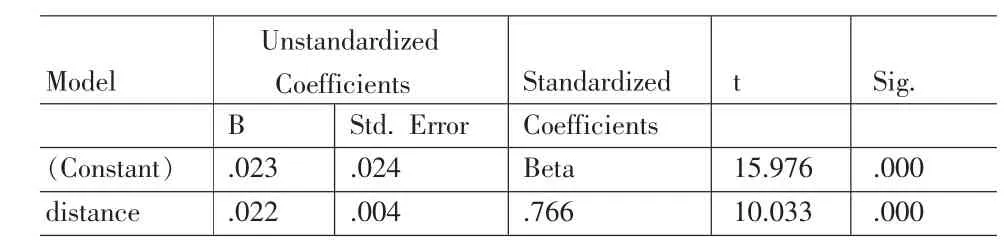
表10 全速行驶回归系数

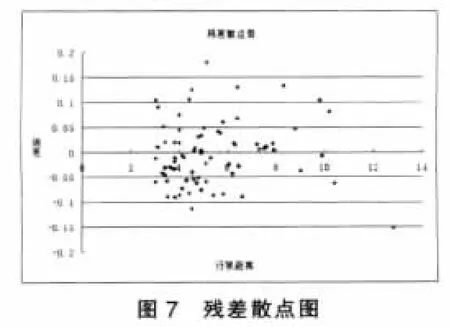
通过残差的频次图和散点图（图7）看到残差基本是在e=0附近随机变化。表明回归模型满足基本假设。因此我们得到全速行驶情形下行驶距离与行驶时间的关系如下：

Tq=0.023+0.022×D

其中D为行驶距离。Tq为行驶时间。

同理对配送行驶情况进行分析，分析结果见表11。

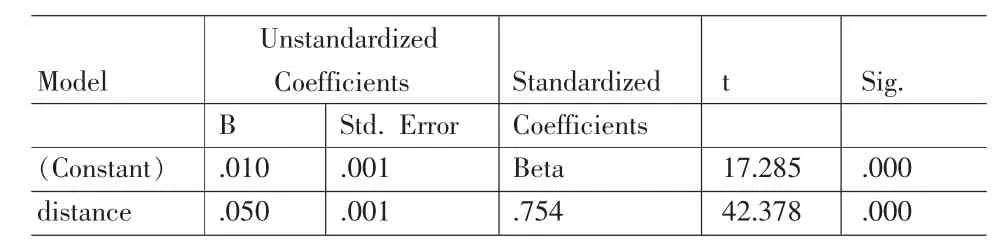
表11 配送行驶回归系数

通过表11看出回归方程及回归系数同样通过了显著性检验。

通过残差的频次图和散点图（图8）看到残差基本是在附近随机变化。表明回归模型满足基本假设。因此我们得到配送行驶情形下行使距离与行使时间的关系如下：

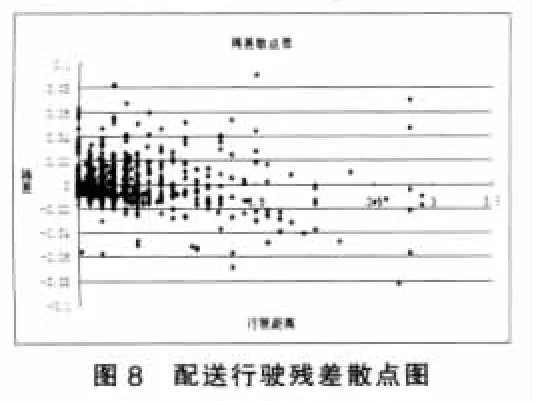
Tp=0.010+0.050×D

其中D为行使距离。Tp为行使时间。

通过上述分析看到不但解决了异方差问题。并对回归方程分析得到一些结论。

结论一，全速行驶回归方程常数为0.023小时即1.38分钟，配送行驶回归方程常数为0.01小时即0.6分钟。说明全速行驶情形下配送司机准备时间较长。

结论二，行驶距离D的倒数可以认为是行驶过程中的速度。全速行驶情形下速度约为45.5公里/小时，配送行驶情形下速度约为20公里/小时。

3 结论

通过以上分析，我们得到配送工作中每个客户的服务时间是独立变量，并均服从同一正态分布。因此我们用该分布的期望代表每一户的服务时间。而行驶时间与行驶距离具有强相关关系，并得到了行驶时间与行驶距离的回归方程，通过线路中的行驶距离可以利用回归方程估算出所需的行驶时间。

综上所述，可以利用配送区域内总期望工作时间作为配送区域工作量的衡量单位。配送工作分为行驶和服务，我们就用行驶时间和服务时间来计算配送区域总工作时间。配送区域内总工作时间如下，其中Tarea为配送区域内总工作时间，单位为小时。N1为配送区域内电子结算客户数量，N2为配送区域内非电子结算客户数量。D1为配送车辆由配送中心到第一个客户的距离加最后一个客户到配送中心的距离，D2为配送车辆配送过程中经过的各配送点的距离之和。

Tarea=N1·0.0195+N2·0.0713+0.023+0.022×D1+0.01+ 0.05×D2

[1]Van K M．Information System Engineering:a Formal Approach [M]．London:Cambridge University Press,1994．

[2]陈子侠,蒋长兵．杭烟物流送货线路的划分模式与算法研究[J]．系统工程理论与实践，2004，（3)．

[3]陈子侠．配送线路划分与电子排单系统建模与算法研究[D]．上海交通大学博士学位论文，2006．

[4]卢纹岱．SPSS for Windows统计分析（第3版）[M]．北京：电子工业出版社，2007．

[5]魏宗舒．概率论与数理统计教程[M]．北京：高等教育出版社，2005．

[6]赖国毅，陈超．SPSS 17中文版统计分析典型实例精粹[M]．北京：电子工业出版社，2010．

(责任编辑/浩天)

F224.9

A

1002－6487（2011）06－0172-04

国家自然科学基金资助项目（79970101，70941013）；国家社会科学基金资助项目（08BJY069）；北京科技大学优势学科创新平台资助项目

谷炜（1982-），男，辽宁锦西人，博士研究生，研究方向：运营管理。