数据包错序的多包传输网络控制系统研究

黄 玲，陈东彦，王攀宇

(哈尔滨理工大学应用数学系，哈尔滨150080)

现代系统中，传感器、控制器、执行器和被控对象常常是通过网络相连，这样的系统被称为网络控制系统(Networked Control System，简称NCS).尽管其有很多的优点和广泛的应用，但由于网络拥塞、多路径传送、连接中断和节点冲突等因素的存在，在数据传输过程中数据包到达目标节点的顺序常会与发送时的顺序不同，这就是所谓的数据包错序[1].许多传统控制技术不能直接应用，而且导致系统不稳定或性能下降.

目前，很少有关于数据包错序的文章.文献[2]为解决错序问题，给数据包附以时间戳标记，使其按照正确的传输时间排序，对于没有到达的数据包利用估计器重新估计状态值，以补偿乱序或丢包等给系统带来的影响.文献[3]针对时延、丢包和错序等非理想网络状况建立连续时间系统模型，引入NCS最大允许综合界解决错序现象.文献[4]给出次优化允许等价时滞界的定义，把网络问题作为控制器设计的参数，为提高网络服务质量提供了有效方法.文献[5]考察的是具有多时延的离散系统，并设计了一种最优控制器来补偿时延给系统带来的影响，但没有考虑错序问题.

本文考虑的是一类含有多个传感器、一个执行器和一个控制器的NCS，在时延小于一个采样周期的情况下研究数据包在传输时发生的错序问题.建立不确定离散线性系统模型，利用Lyapunov方法推出闭环系统渐近稳定的充分条件，并给出算例验证方法的有效性.

1 系统建模

图1 数据包错序的多包传输NCS框图

在本文中假定以下条件:

1)控制器和传感器采用时间驱动方式，执行器采用事件驱动方式，系统采样周期为T;

2)系统中含有n个传感器，每个传感器节点数据都带有不同的状态标识符;

3)网络仅存在于控制器与传感器之间，时延小于一个采样周期.

考虑离散线性系统

如图2所示，表示t=3和t=4时刻缓存区的数值.

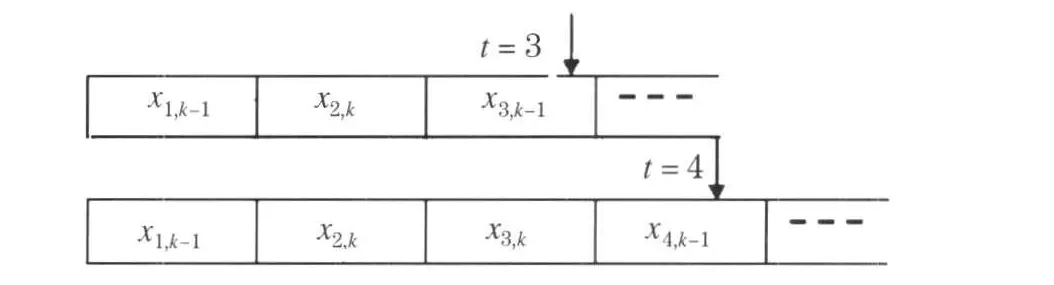
图2 t=3和t=4时刻缓存区的数值

引入矩阵Fk，令

在采样时刻k，控制器输入为

则系统模型描述如下:

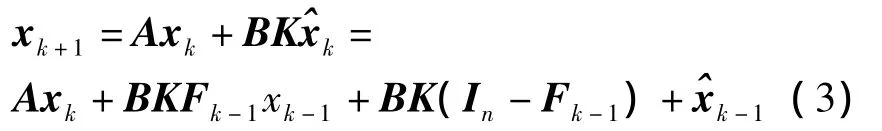
2 稳定性分析

首先，在以下部分给出两个引理.

引理1给出对称正定矩阵P，对称矩阵Q和矩阵A，则A+PA+Q＜0等价于或

引理2[6-7]实矩阵W，M，N和F(k)，其中F(k)满足FT(k)F(k)≤I，W是对称矩阵，则W+NTFT(k)MT+MF(k)N＜0当且仅当存在一个标量ε＞0满足

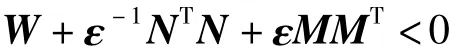
以下给出本文主要结果.

定理1对于具有错序、时延和丢包的NCS模型(3)，设系统状态反馈控制律如果存在正定对称矩阵和标量 ε ＞0，满足下面的不等式:则系统(3)是渐近稳定的.

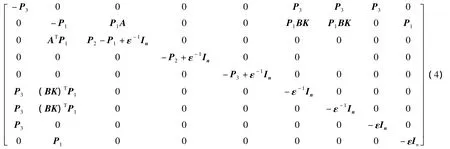
沿着系统(3)的轨迹对Vk作差分，得

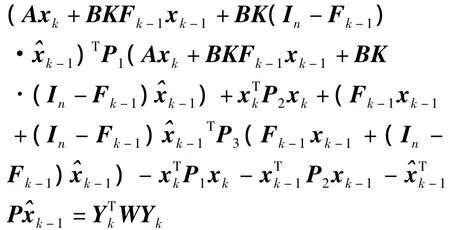
其中

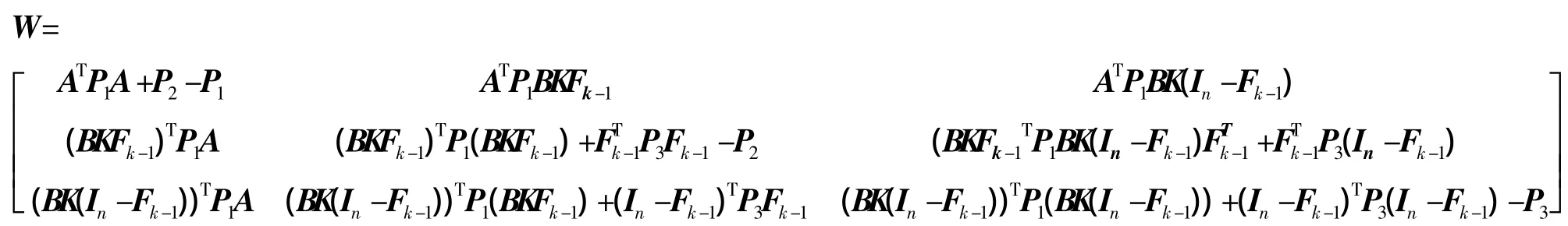
利用Lyapunov稳定性理论，如果ΔVk＜0，则系统(3)是渐近稳定的.而ΔVk＜0的充分条件是W＜0.注意到

由引理1，W＜0当且仅当

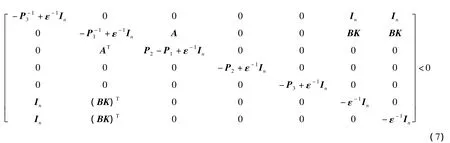
由引理1，上式等价于不等式(4).证毕.

3 算例仿真

考虑如下具有错序、时延和丢包的NCS.

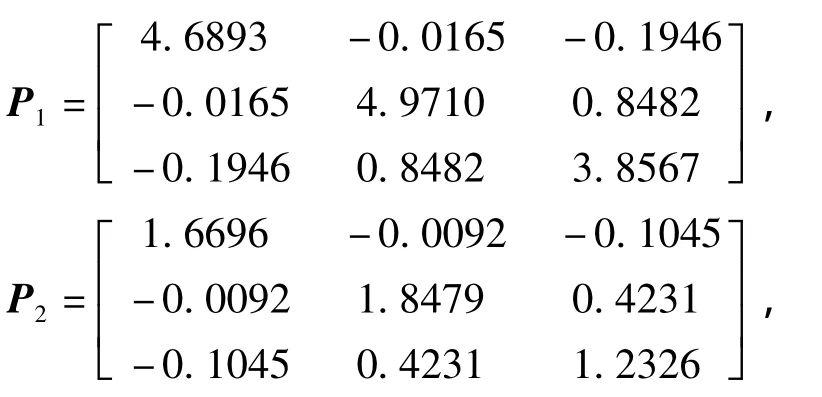
则NCS是渐近稳定的.

如果系统初始值为[x1x2x3]=[5 1-1]T，仿真结果如图3所示.

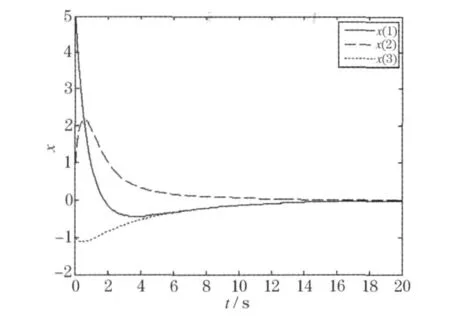
图3 闭环NCS状态响应曲线

4 结语

在研究具有时延和数据丢包的多包传输NCS的同时，加进了另一种非理想网络状况——错序.假设每个数据都带有状态标识符，并在控制器前端安放一个存储器，在存储器中设置有缓存区，其目的是让数据到达时按照原有的标识排序，然后建立NCS模型并分析稳定性.

[1]严怀成.网络控制系统的分析与综合[D].武汉:华中科技大学，2007:5-7.

[2]SCHENATO L.Optimal Estimation in Networked Control Systems Subject to Random Delay and Packet Loss[C]//Proceedings of the 45th IEEE Conference on Decision and Control Manchester Grand Hyatt Hotel，USA，2006:5615-5620.

[3]周映江，李训铭，梁 华.不确定时滞网络控制系统的状态反馈控制[J].控制理论与应用，2010，27(2):221-225.

[4]彭 晨，岳 东，彭丽萍.网络控制中基于LMI的次优化允许等价时滞界研究[J].系统仿真学报，2007，19(2):369-372.

[5]LIAN F L，JAMESM，DAWN T.Optimal Controller Design and Evaluation for A Class of Networked Control System with Distributed Constant Delays[C]//Proc of the American Control Conference，Anchorage，AK，2002:3009-3014.

[6]LIX，SOUZA C E.Delay-depended Robust Stability and Stabilization of Uncertain Linear Delay Systems:A Linear Matrix Inequality Approach[J].IEEE Transactions on Automatic Control，1997:1141-1144.

[7]张立众.基于ARM的工业以太网控制器的设计与应用[J].哈尔滨商业大学学报:自然科学版，2010，26(5):583-585，591.