基于遗传算法的组卷方法研究
王民川
郑州广播电视大学,河南郑州 450007
考试是一项“测量工程”。从统计学的角度来看,考试是一种抽样测量,通常我们告诉学生的应考内容是考查的总体,而试题实际考查到的内容则是我们从总体中抽取的样本。要提高考试质量,在实施考试之前,先要进行设计。为了更好地普及计算机命题,有必要研究一种采用科学、先进的组卷方法来实现快速、高效、科学组卷。本文着重对遗传算法在自动组卷中的应用研究,通过对遗传算法理论的研究,探讨一下遗传算法以解决智能选题成卷的问题。
1 自动组卷算法研究
国内外的许多科研单位、学校机构都在对组卷系统进行研究[1]。虽然组卷系统是一个被探讨了很长时间的问题,但至今还没有一个很好的解决其自动出题的算法方案。以前所采用的算法大多是随机选取和回溯试探法,他们虽然都能最终组出试卷,但是在实际的操作过程中,却发现他们不是耗费的时间很大就是容易进入死循环。
2 遗传算法概述
遗传算法GA[2](Genetic Algorithm)是一种新型的、模拟自然界生物进化过程的随机搜索、优化方法。他是模拟达尔文的遗传选择和自然淘汰的生物进化过程的计算模型,是由美国Michigan大学的JohnH.Honlland教授于1975年首先提出来的。他采用简单的编码技术来表示各种复杂的结构,并通过对一组编码表示进行简单的遗传操作和优胜劣汰的自然选择来指导学习和确定搜索的方向。由于他采用种群的方式组织搜索,这使得他可以同时搜索解空间内的多个区域。而且用种群组织搜索方式使得遗传算法特别适合大规模并行。
3 基于遗传算法的组卷方法
首先,确定考试时间KSSJ、试卷的满分值MFZ和所用的题型以及各种题型的题目和分数,而且对一种考试而言,这种题型一一分数分布曲线LT常保持相对稳定,如英语等级考试、各种计算机等级考试等都是这样。
其次,获取难度一一分数分布曲线LD、内容一一分数分布曲线LC,教学要求度一一分数分布曲线LR及其各自允许的误差,曲线LC,LR及其允许的误差均由用户给出。曲线LD在很大程度上决定了考试成绩的分布,是很重要的一条曲线。
4 自动组卷的遗传算法设计与实现
4.1 染色体编码及群体的初始化
经典遗传算法采用二进制编码,用1表示该题被选中,0表示该题未被选中,这种编码简单明了,但是进行交换等遗传操作时,各题型的题目数难以精确控制,而且,当题库中题量很大时,编码很长。
4.2 适应度函数
在遗传算法中,以适应值大小来区分群体中个体的优劣。一般情况下适应值越大的个体越好,适应值越小的个体越差。
4.3 遗传算子设计
1)选择算子
采用期望值模型选择机制,即先用公式1计算群体中各个个体期望被选中的次数:
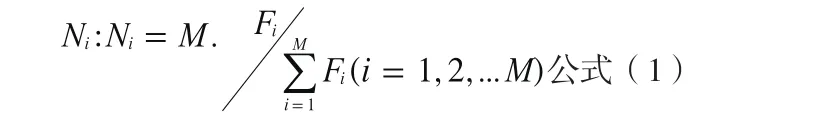

2)交叉算子
将以上选出的个体进行两两随机配对,对每一对相互配对的个体采用有条件的“均匀交叉”,即两个配对个体的每一个基因座上的基因都按设定的交叉概率Pc和一定的条件(确保交换后个体仍是有意义的组合)进行交换,产生两个新个体。
3)变异算子
由于普通的变异操作可能会使用户指定范围外的题目出现在染色体中,也会使各题型的题目数难以保证,本文采用有条件的变异算子,即每个个体的每一个基因座上的基因都按设定的变异概率Pm在一定范围内变异。
4)最优保存策略
进行了选择、交叉、变异操作后,比较新一代的最好个体与上一代的最好个体的适应值,如下降,则以上一代最好个体替换新一代的最差个体。
5)算法实现
确定参数:最大代数MaxGene,群体规模Pop Size,交叉概率Pc,变异概率Pm;
接收用户的组卷要求:
产生初始群体;
当前代数Gene=0;
计算群体中各个体的适应值;
while(Gene { 根据个体适应值及选择策略从当前群体中选择生成下一代的父体; 执行交换操作和变异操作生成新一代群体; 计算新一代群体中各个体的适应值; 比较新一代的最好个体与上一代的最好个体的适应值,如下降,则以上一代最好个体替换新一代的最差个体: 输出当前代数,群体的平均目标函数,最好个体的目标函数值; 输出最好个体的编码,计算各难度级别的分数等指标,输出这些指标的值并与用户的要求值相比较。 从难度、区分度、信度、效度是评介成卷合理性的有效指标,尽管这些指标是利用试卷的应试结果进行分析,我们在组卷时没有应试结果,但我们应当了解其计算方法,以便指导我进行科学、合理性组卷。试卷分析涉及的理论如下所述[3]。 本系统要求所开发的组卷功能体现遗传算法的应用,其技术指标,如:难度、所用时间等,存放在试题库中,而试题库管理系统则采用合理的选题算法,对题库中的题目从难度进行控制选题,从而生成符合测试要求的试卷。 随着计算机考试系统的不断普及,基于遗传算法的自动组卷技术越来越成为计算机辅助测试中人们研究的一个热点。文章基于对遗传算法的研究,只应用了组卷系统的几个变量,至于要自动生成完全符合标准化考试的试卷,则算法中应用加入更多的组卷系统变量,才能高效、科学地满足组卷要求。由于计算量大,所以在运行过程中程序出现了假死现象,这个问题值得继续研究。 [1]王小平,曹立明.遗传算法[M].西安:西安交通大学出版社,2002,6. [2]李敏强,等著.遗传算法的基本理论与应用[M].北京:科学出版社,2003,3.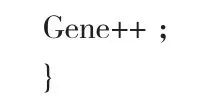
5 成卷的技术指标
6 组卷系统分析
7 结论

