关于热机循环效率的讨论

汤庆国，沈国浩

（蚌埠学院 数理系，安徽 蚌埠 233030）

关于热机循环效率的讨论

汤庆国，沈国浩

（蚌埠学院 数理系，安徽 蚌埠 233030）

讨论了卡诺定理的含义，证明了奥托循环和其他可逆非卡诺循环的效率低于同温度之间可逆卡诺循环的效率，这可作为卡诺定理的推论，纠正了一种对卡诺定理的模糊认识.

热机；循环效率；卡诺定理

从热机诞生后，人们就致力于研究热机的循环效率问题，探索提高热机效率的途径.法国工程师卡诺在1824年提出了一种由两个等温过程和两个绝热过程构成的热机循环模式，即卡诺循环，并总结出关于其循环效率的卡诺定理.在热机研究中做出重要贡献.在教学中有些人认为卡诺定理指出了热机循环的效率上限[1]，我们认为这是不够准确的，因为卡诺定理只是讨论了卡诺循环的效率，并未涉及其他循环模式的效率，本文就此展开一些讨论.

1 卡诺定理的表述[1,2]

（1）在相同的高温热源和相同的低温热源之间工作的一切可逆热机，其效率都相等，与工作物质无关.

（2）在相同的高温热源和相同的低温热源之间工作的一切不可逆热机，其效率都小于可逆热机的效率.

由上述定理表述及定理的证明过程[2]可知：此定理所说的可逆热机和不可逆热机都是做卡诺循环的热机，并没有讨论以其他循环模式工作的热机的效率，也就无从得出热机循环的效率上限.

2 奥托循环的效率

四冲程汽油机的理想循环模式由绝热压缩、等体吸热、绝热膨胀和等体放热四个过程构成，称为奥托循环，如图1所示.

对于两等体过程BC和DA，有

对于两绝热过程AB和CD，有

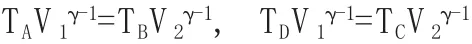
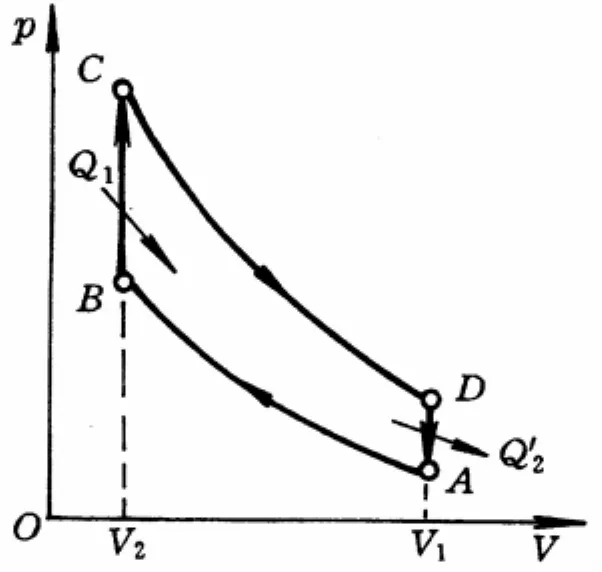
图1 奥托循环

其循环效率为：

则TC和TA分别是此奥托循环过程中工作物质的最高和最低温度.

若有一卡诺循环热机同样工作在最高温度TC和最低温度TA之间，则其效率为

由（1）（2）（3）式可得 ηC>ηo

3 可逆非卡诺循环的效率小于同温度之间可逆卡诺循环的效率

下面我们用温熵图来比较任意一个可逆非卡诺循环的效率与同温度之间可逆卡诺循环的效率[3].

如图2所示，在两条等温线之间给定任意一个可逆非卡诺循环am bna，设其循环效率为η.我们可以做一个相应的可逆卡诺循环ABCDA，设其循环效率为ηC.循环am bna中am b过程吸热，吸收的热量等于曲线am bEFa包围的面积SambEF即：

图2 温熵图

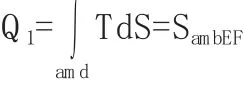
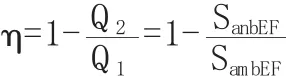
所以 ηC>η

此结论可作为卡诺定理的推论.

4 不可逆循环的效率小于同模式可逆循环的效率

对于可逆循环，因为不存在摩擦等耗散因素，所以循环一周系统对外作的净功等于吸收的热量Q1减去放出的热量Q2

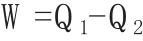
对于不可逆循环，因为存在摩擦等耗散因素，设循环一周耗散的热量为Q3>0,所以系统对外作净功

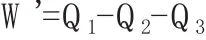
可见 η>η'.

5 结束语

通过以上讨论可知，卡诺定理是在研究热机的卡诺循环时得出的结论，并未涉及其他循环模式的效率，因此不能说其给出了热机循环的效率上限.本文第3、第4部分的讨论证明了可逆卡诺循环的效率是热机循环效率的上限，这可作为卡诺定理的推论.

〔1〕罗益民，余燕．大学物理（下）（第 2 版）[M]．北京：北京邮电大学出版社，2008：183－184．

〔2〕赵凯华，罗蔚茵．新概念物理教程：热学[M]．北京：高等教育出版社，1998：180－182．

〔3〕刘凤鳌．卡诺定理及其推广的简捷证明[J]．工科物理，1994（3）：18－19．

〔4〕黄晓圣，王剑．关于卡诺定理证明的教学探讨[J]．大学物理，2002，21（11）：24－25．

〔5〕熊吟涛，等．热力学[M]．北京：人民教育出版社，1979．

O414

A

1673-260X（2011）10-0018-02