光场与纠缠原子依赖强度耦合系统场熵的演化
杨猛 刘海燕
聊城大学 物理科学与信息工程学院, 山东 聊城 252059
光场与纠缠原子依赖强度耦合系统场熵的演化
杨猛 刘海燕
聊城大学 物理科学与信息工程学院, 山东 聊城 252059
在考虑原子与光场依赖强度耦合光子共振相互作用的条件下,研究了粒子数态光场与纠缠双原子依赖强度耦合系统场熵的演化特性,并借助于数值运算,讨论了双原子纠缠度及光场强度对场熵演化的影响。研究结果表明,双原子纠缠度的变化影响场熵的平均值,而初始光场的强度则影响场熵演化的振荡特性。
1 引言
量子纠缠现象是量子信息理论[1-3]的基础。为了定量地描写量子纠缠,人们对量子纠缠度进行了大量地研究[4-7]。对于两个子系统组成的复合系统,纯态纠缠度的定量化已经完成,其纠缠度等于任一子系统约化密度矩阵的Von Neumann熵。熵自动包含了量子系统密度矩阵的全部统计矩,它既是一种十分灵敏的量子态纯度和光场-原子关联程度的量度,也是解释量子系统动力学特征的重要工具[8]。场(原子)熵的时间演化反映出关联程度的演化特性,熵越高,关联越强。因此,考察光场-原子相互作用系统熵的演化行为,可以获得该系统纠缠特性的有用信息。
依赖强度耦合J-C模型(J-C模型)是Buck和Sukumar为反映光场与原子相互作用对光场强度的依赖性而提出的理论模型。众多学者对该模型作了多种推广[9],但有关光场与纠缠原子依赖强度耦合系统量子特性的研究尚少涉及。本文应用量子熵理论,研究了粒子数态光场与纠缠双原子依赖强度耦合系统的场熵演化规律,发现双原子纠缠度和光场强度对场熵的时间演化行为均有非常重要的影响。
2 模型及理论推导
考虑纠缠双原子中一个二能级原子进入腔场,而另一个远离腔场。设原子与光场间的耦合系数为ε,在旋波近似下,系统的哈密顿量为:

若光场处于粒子数态,则原子-光场相互作用系统初始时刻的态矢可表示为

3 场熵的演化特性
由于光场和原子在初始时刻均处于纯态,彼此无关联,因此光场-原子系统的熵S为零且不随时间变化。在t>0的任何时刻,光场与原子的熵相等,即。因此,可以利用原子约化密度矩阵求出系统场熵的表达式。
根据态矢表达式(10),容易得到原子约化密度矩阵为
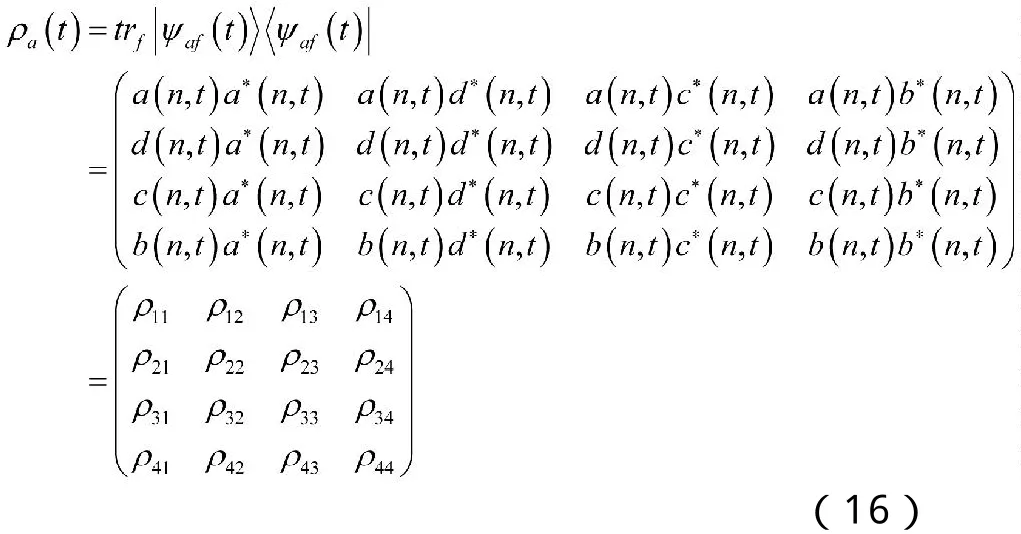
系统的场(原子)熵为


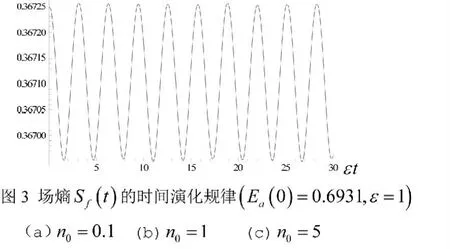
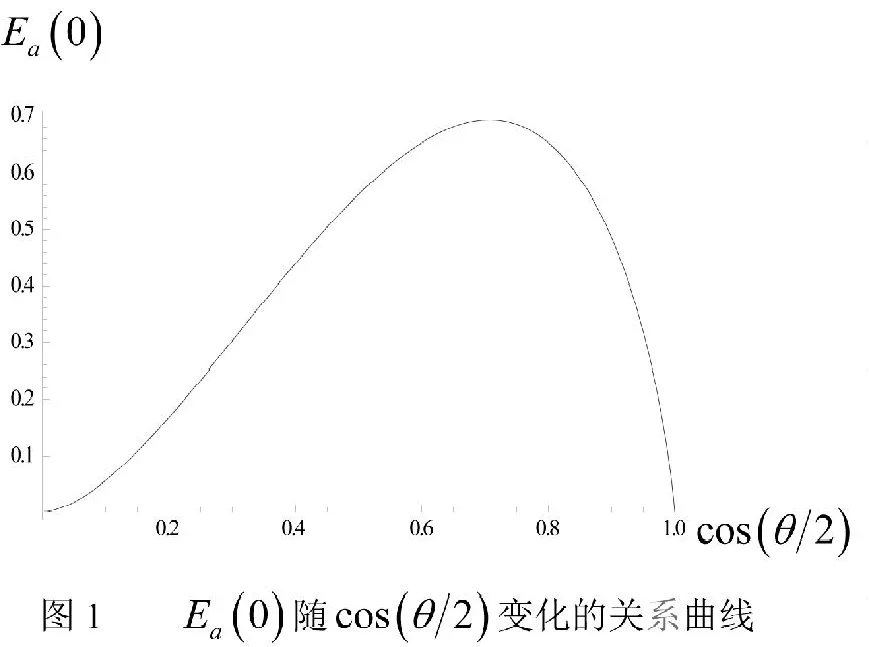
为了揭示系统场熵的时间演化特性,分别选取不同的双原子初始纠缠度Ea(0)和初始光场强度n0作数值计算,得到如图2和图3所示的结果。

对于光场-原子相互作用系统,场熵演化呈不规则振荡是单光子过程的基本特征,而场熵演化呈规则振荡则是双光子过程的基本特征。上述结果表明:初始光场强度的变化不仅影响光场-原子系统纠缠度的强弱,还影响场熵演化的振荡特性。
4 结论
本文运用全量子理论,研究了粒子数态光场与纠缠双原子依赖强度耦合系统场熵的演化特性,着重讨论了双原子系统初始纠缠度和初始光场强度对场熵演化行为的影响。
1)光场-原子相互作用系统中光场-原子的纠缠与双原子初始纠缠度是相互关联的。双原子系统初始纠缠度大时,则场熵的平均值也较大,从而光场-原子纠缠度也大;双原子系统初始纠缠度小时,则场熵的平均值也较小,从而光场-原子纠缠度也小。
2)初始光场强度不仅影响光场-原子系统纠缠度的强弱,还影响场熵演化的振荡特性。当初始光场强度较弱时,场熵随时间的演化呈不规则振荡,光场-原子之间的相互作用主要表现为单光子跃迁过程;当初始光场强度较强时,场熵随时间的演化表现为较规则振荡,光场-原子之间的相互作用主要表现为双光子跃迁过程。
[1] Bennett C H, Brassard G, Crepeau C, et al. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels [J]. Phys. Rev.Lett. , 1993, 70: 1895
[2] Horodecki R, Horodecki M.Information-theoretic aspects of inseparability of mixed states [J]. Phys
Rev A, 1996, 54: 1838~1843.
[3] Shor P W. Scheme for reducing decoherence in quantum computer memory[J]. Phys. Rev., 1995, A52:R2493
[4] Bennett C H , DiVincenzo D P,Smolin J A , et al. Mixedstate entanglement and quantum error correction[J]. Phys. Rev., 1996, A54:3824
[5] Vedral V, Plenio M B, Rippin M A,et al. Quantifying entanglement [J].Phys. Rev. Lett. , 1997, 78: 2275
[6] Horodecki M, Horodecki P, Horodecki R. Limits for entanglement measures [J].Phys. Rev. Lett. , 2000, 84: 2014
[7] R.R.Schlicher. Jayens-Cummings model with atomic motion [J].Opt.Commun.,1989,70 (2):97~102
[8] Vedral V, Plenio M B. Entanglement measures and purification procedures [J].Phys. Rev., 1998, A57:1619
[9]黄春佳,周明,厉江帆.单模辐射场与耦合双原子相互作用系统中场熵的压缩特性 [J]. 物理学报. 2002,51(4):805-808
A
10.3969/j.issn.1001-8972.2011.02.012
国家自然科学基金(10574060)、山东省自然科学基金(Y2008A23)和山东省高校科技计划(J09AL07)资助项目
量子光学;场熵演化;纠缠双原子;依赖强度耦合
中国分类号:0431.2

