直接驱动XY平台零相位误差跟踪新型交叉耦合控制*

赵希梅 郭庆鼎 翟惠萍

(沈阳工业大学电气工程学院，辽宁沈阳 110870)

随着复杂型面零件加工质量要求的不断提高，轮廓加工精度已成为其重要的精度指标。XY平台系统的轮廓误差是由轮廓运动所涉及的X、Y两轴的位置误差共同决定。在直线电动机直接驱动XY平台的系统中，参数不确定性、进给系统的机电延迟以及两轴驱动系统参数不匹配等因素对XY平台的轮廓加工精度产生重要的影响。

传统多轴控制器的控制方法，是采取各轴独立控制方式。对于轮廓误差的改善是增加位置跟踪控制的精度，降低跟踪误差，进而间接地降低路径误差。此种控制方式除了PID控制外，有前馈控制、预见控制和零相位误差跟踪控制等。Masory提出速度前馈控制以改善跟踪误差，加入前馈控制补偿，只补偿被控系统的传递函数，使输入与输出的传递函数之积为1，但由于相位的前移而使系统频宽增大，且可让位置跟踪误差减小，以补偿参数不一致所造成的影响。Tomizuka提出零相位误差跟踪控制法则，使得理论上跟踪误差为零。而以上的方法均需了解各轴的参数，才能设计最佳的控制器。由于各轴的参数不一致，且系统模式经常是非线性时变的，因而不易准确测出系统的参数。而又有负载干扰对系统的影响，使得前馈控制等方法的鲁棒性较差，无法有效地改善系统的跟踪误差。

为提高XY平台系统的轮廓精度，许多研究方法侧重于设计良好的反馈控制器以减小单轴的跟踪误差，进而减小整个系统的轮廓误差，但这种方法对提高轮廓精度并不总是有效的。Koren首先提出了交叉耦合控制器(cross－coupled controller——CCC)以直接减小轮廓误差的思想，其方法是将整个多轴运动系统看成是一个单一系统而含多个变数，借由各轴间彼此的影响来相互补偿，使响应快的轴减慢，响应慢的轴加快，增加两轴的匹配程度，进而减小其路径误差。文献［4－5］设计了CCC以提高多轴数控机床的轮廓精度。已有的研究表明，传统交叉耦合控制系统较之常规的非耦合控制系统有更好的轮廓精度，但传统交叉耦合控制器不足之处在于对任意曲线轨迹轮廓误差系数的计算量较大，控制器设计复杂。

本文采用永磁同步直线电动机(PMLSM)直接驱动XY平台，利用零相位误差跟踪控制与新型交叉耦合控制相结合的策略对两轴的运动进行协调控制，实现跟踪精度与轮廓精度的同时提高。在单轴控制回路中引入ZPETC以补偿伺服系统的滞后效应，提高系统的跟踪精度。新型交叉耦合控制器作用于两轴之间，将轮廓误差作为直接被控目标，根据各轴的反馈信息，进行实时补偿控制，可有效提高轮廓精度。

1 XY平台的轮廓误差分析

考虑XY平面的圆弧跟踪，由两台PMLSM直接驱动轴向相互垂直的XY两轴进行平面运动，以完成精密轨迹运动。

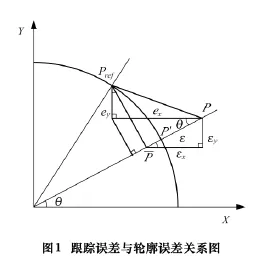
Pref为轨迹上的参考位置，P为刀具实际位置，要求P到轨迹上P'的距离最小，而以来近似圆弧的轮廓误差。图1为其相关几何关系图，ε为轮廓误差，e为跟踪误差，εx、εy分别为轮廓误差在X轴和Y轴上的分量，ex、ey分别为跟踪误差在X轴和Y轴上的分量。

轮廓误差ε为

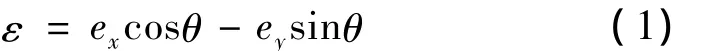
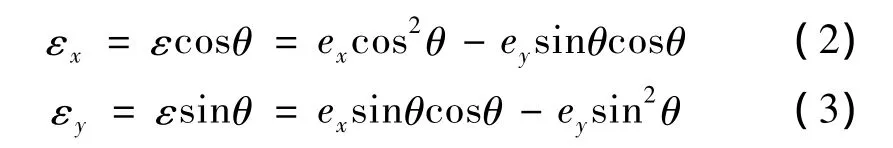
目的是希望实际加工位置能达到参考位置，所以除了补偿各轴的跟踪误差ex、ey外，必须另外补偿［－εx– εy］T的向量，－ εx和 － εy的大小为

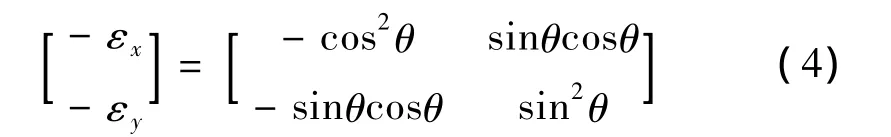
使得实际加工点达到参考指令点，以使得合成轨迹趋近于预设的轮廓。

2 XY平台系统设计

基于ZPETC和新型交叉耦合控制的系统框图如图2所示，Xd和Yd、Xa和Ya分别表示各轴的位置输入和输出，εx和 εy为X、Y轴的扰动项，Ⅰ、Ⅱ表示X、Y轴的零相位跟踪控制器，Ⅲ表示新型交叉耦合控制器。

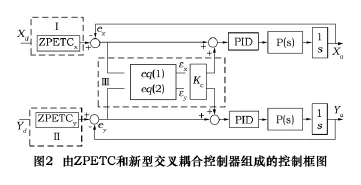
2.1 零相位误差跟踪控制(ZPETC)

XY平台驱动系统在跟踪控制时，由于存在着电磁惯性和机械惯性使输出响应和输入指令之间存在滞后现象，两信号间存在着较大的相位误差。为补偿时间延时对系统跟踪精度的影响，采用Tomizuka提出的零相位误差跟踪控制(ZPETC)［7］，它是一种结合零、极点对消和相位对消，能在较大的带宽范围内对闭环动态系统进行逆处理的前馈控制［8］。

下面将针对包含不可对消零点的系统来设计ZPETC。考虑如下离散闭环传递函数

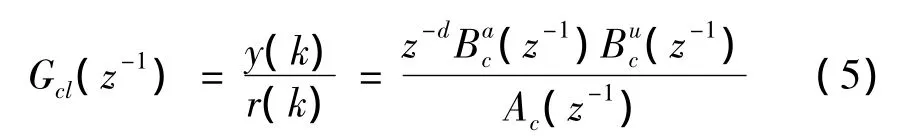
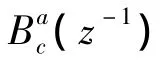
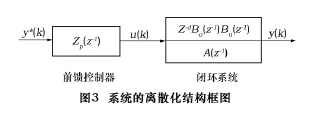
所设计的ZPETC如图3及式(6)所示。

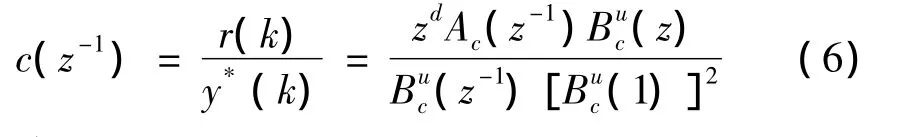
所以由y*(k)到y(k)的传递函数为

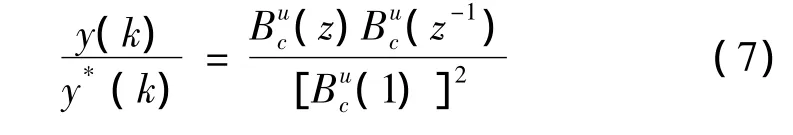
当z=ejωT时，输入指令与输出响应之间不存在相位差，可达到零相位跟踪控制。当ω→0时，z→1，所以系统在甚低频时有y(k)→y*(k)。上式的相位差在整个频域内趋近于零，在一定频带内其幅值接近1。

2.2 新型交叉耦合控制

传统轨迹跟踪控制方法为将各轴的控制器分开设计，而且轴与轴之间各自独立控制，彼此之间不互相影响，由于轴与轴之间动态特性的不同，且系统模型通常呈现时变现象，因此无法满足轮廓误差对精度的要求。因此本文研究交叉耦合控制系统，利用直角坐标平面轨迹图，由几何关系推导出必须额外补偿的控制量，借助这种补偿方式人为地使各轴之间产生互相影响，使响应快的轴变慢，响应慢的轴变快。

2.2.1 传统交叉耦合控制

图4为交叉耦合控制结构框图，其中eq(1)和eq(2)即为上述的式(2)和(3)。

由图4可以明显得知除了各轴的跟踪误差外，中间的交叉耦合控制器计算出轮廓误差的X轴与Y轴分量 εx、εy，分别乘以交叉耦合控制器增益Gx、Gy后，再补偿到X轴与Y轴上，至于交叉耦合控制器的增益Gx、Gy调整法则，目前并没有一定的规则可循，只知道和规划路径存在一定的关系，因此一般使用常数增益来调整:

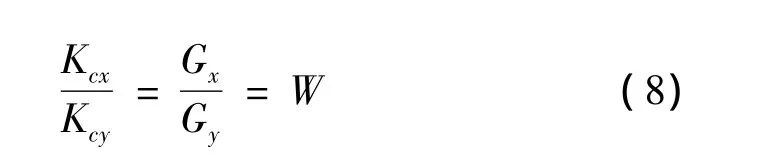
其中:Kcx、Kcy为各轴PID参数中的Kp值;W为一常数定值。另外也有利用PID控制器取代Gx、Gy的一般常数增益，并使用试凑法求得最小轮廓误差的PID参数。

2.2.2 新型交叉耦合控制

新型交叉耦合控制结构框图如图2中虚框Ⅲ所示。根据交叉耦合原理，除了各轴的跟踪误差ex、ey外，必须另外补偿［εxεy］T的向量使得合成向量接近于预设路径与参考指令点。参考Koren提出交叉耦合控制结构，另外补偿的值为经过一常数增益，加上单轴控制回路运算完的值，再输出命令给电动机，即使以PID控制器取代常数增益值，依然必须针对不同条件作PID参数的修正。

然而从直观上看，可以让轮廓误差补偿值先和跟踪误差作运算，再经由PID控制器处理。因此本文在补偿运算上作部分修改，让补偿值εx和跟踪误差ex先作加减运算，其中因为跟踪误差和轮廓误差补偿值非为同等地位参数，因此轮廓误差补偿值需先乘一权重常数，才得以和跟踪误差作运算，之后再经PID控制器处理，然后输出给电动机。

在传统PID交叉耦合控制结构中，控制器设计方法为利用自动调整求得X、Y轴上的PID参数，再依实验数据做稍微修正，然后再利用试凑法求取交叉耦合控制器参数。本文中将交叉耦合运算位置稍微变动后，就可以比原来结构更容易设计控制器参数，且得到更好的效果。

交叉耦合控制器(Kc)的设计，一般而言为一大于0的常数，理论上随着Kc值增大，轮廓误差将逐渐减小至0;实际上Kc会有一极限值，当Kc大于极限值时，会发生实际轨迹在参考轨迹左右快速震荡，并造成机械台振动。因此当一般常数Kc无法达到要求的精度时，可以将Kc设计为一时变参数，使Kc与轮廓误差成正比，借以进一步修正轮廓误差。这里所谓时变参数方法为先求出非耦合时的轮廓误差曲线，利用Curvefitting求得时间和误差的曲线方程式，再将方程式放到Kc的位置，取代成为时变的参数。

3 仿真结果及分析

为了验证所提出的控制方法的有效性，进行了圆弧轮廓控制的仿真和实验研究，采用两台参数相同的PMLSM作为XY平台的驱动部件进行研究。电动机参数为Mn=11.0 kg，B=8 N·s/m，Kf=29 N/A，圆弧轨迹跟踪条件为:进给速率200 mm/s，角速度为2π，圆弧角度为180°。Kp=13.96，KI=232.69，KD=0.21，Kc=0.3。图5、图6分别为PID+CCC、ZPETC+CCC和ZPETC+新型CCC三种情况下的圆弧轮廓误差仿真和实验曲线。其中，曲线a表示在PID+CCC条件下的轮廓误差;曲线b表示在ZPETC+CCC条件下的轮廓误差;曲线c表示在ZPETC+新型CCC条件下的轮廓误差。从仿真和实验结果可以明显地看出，在相同的条件下，采用ZPETC+新型CCC的控制策略最佳，能提高系统的跟踪性能，并能消除各坐标轴间参数不匹配的影响，能十分有效地减小轮廓误差。从仿真曲线看轮廓误差达到170 μm左右，实验曲线看轮廓误差达到230 μm左右，得到很好的效果。

4 结语

基于ZPETC与新型CCC相结合的控制策略有效地削弱机械系统的时间延迟效应、负载扰动以及两轴驱动系统参数不匹配等因素对直线电动机直接驱动XY平台轮廓加工精度的影响。ZPETC实现了快速准确跟踪;新型CCC作用于两轴之间，将轮廓误差作为直接被控量进行实时补偿控制，解决了两轴驱动系统参数不匹配问题，有效地提高了轮廓精度并简化了控制器设计。此控制方案在保证系统跟踪性和鲁棒性的同时大幅度减小了系统轮廓误差。仿真和实验结果表明了此方案是有效的。

［1］王广炎，张润孝，帅梅，等.数控机床的轮廓误差的控制［J］.机床与液压，1999(6):59－61.

［2］Yan Zugen，Sun Lining，Huang Bo.Research of a novel XY － table based on error compensation［J］.Proceedings of the IEEE International Conference on Mechatronics ＆ Automation.Niagara Falls，Canada，2005(1):61－64.

［3］丛爽，刘宜.多抽协调运动中的交叉耦合控制［J］.机械设计与制造，2006，10:166－168.

［4］Sun Dong，Shao Xiaoyin，Feng Gang.A model－free cross－ coupled control for position synchronization of multi－ axis motions［J］.Theory and Experiments.IEEE Transactions on Control Systems Technology，2007，15(2):306－314.

［5］Cheng Ming－Yang，Lee Cheng－Chien.Motion controller design for contour－following tasks based on real－time contour error estimation［J］.IEEE Trans.on Industrial Electronics，2007，54(3):1686 －1695.

［6］蓝益鹏，郭庆鼎.直线电动机伺服系统的鲁棒H∞控制［J］.电工技术学报，2003，18(5):54－58.

［7］富强，吴云洁.基于QFT和ZPETC的高精度鲁棒跟踪控制器设计［J］.自动化技术与应用，2004，(23)8:1 －3.

［8］赵希梅，郭庆鼎.为提高轮廓加工精度采用 DOB和ZPETC的直线伺服鲁棒跟踪控制［J］.电工技术学报，2006，21(6):111－114.

［9］Yeh Syh－Shiuh，Hsu Pau－Lo.Estimation of the contouring error vector for the cross－ coupled control design［J］.IEEE/ASME Trans.on Mechatronics，MARCH 2002，7(1):44 －51.

［10］Yang Jiangzhao，Xu Jijie，Li Zexiang.Two－degree－of－ freedom based cross － coupled control for high － accuracy tracking systems［J］.Proceedings of the 3rd Annual IEEE Conference on Automation Science and Engineering，Scottsdale，AZ，USA，Sept 22－25，2007:950－955.