基于Daubechies小波和工件面形误差的机床导轨误差相关性分析*
陈东菊 范晋伟 张飞虎
(①北京工业大学机械工程与应用电子技术学院,北京 100124;②哈尔滨工业大学机电工程学院,黑龙江哈尔滨 150001)
对于机床这种复杂而庞大的结构,其加工精度受到机床几何误差、热误差、切削力以及外界环境等多个误差源的影响,几何运动误差(如导轨直线度,主轴偏摆误差等)主要引起加工结果的低频误差,振动误差(如切削力误差)等主要引起加工结果的高频误差。误差源辨识技术是利用现代科学技术手段,根据机床的误差信息及机床的工作状况,确定误差的性质、程度、类型及产生的部位和机理。辨识方法主要有两种:一种是基于检测仪器的误差辨识;一种是基于工件检测数据的误差辨识。目前对机床误差的辨识,大部分还是利用第一种辨识方法。如用球杆仪检测机床热误差[1],激光干涉仪用于机床误差的测量[2],平面正交干涉测量[3]等。这种方法有一定的弊端,它基本上都是针对静态或准静态误差进行测量的,难以辨识出切削过程中的动态误差,对于可直接测量的误差,会引入单项检测误差;不能直接测量的误差,通过对直接可测误差测量来推导其误差,这样会引入大量推导误差,这些都会对加工结果带来大的影响。Cheung等[4]和Kim等[5]基于工件检测数据对机床误差进行辨识,但他们的研究只单从频域对信号进行傅里叶变换,假设信号是平稳的,其频谱是非时变的。但对于机械振动信号,具有明显的时变非平稳性,其频谱时间有较大变化[6],这样单从频域确定机床误差源的方法已不再适用。
机床加工的实际检测结果表明,加工工件的表面形貌包含各频率范围的低频信号和高频信号。针对这种表面形貌信息,提出一种基于小波变换和特征相关性分析的辨识模型。小波变换是在时间和尺度平面上描述的,是一种多分辨率的分析方法,最大的优点是在时域和频域同时具有很好的局部化性质,既能对信号中的短时高频成分进行准确定位,又能对信号中的低频缓变成分进行精确的趋势分析。可以利用小波的变焦特性,观察和分析在不同尺度下的工件表面形貌。数理统计中,确定两个随机信号之间的相关联程度,一般用相关性函数进行分析[7]。L.Andren 等[8]利用结构特性间的相关性来辨识连续钻孔加工中切削机床的振动信号。Adam G等[9]把选择区域的相关性分析用于机床的故障诊断中。印度学者[10]利用互相关性来支持向量机对脑电图信号进行分类。对于分解出的各种信号的特征分析,因为相关函数是对两个随机信号相关性的测度,这里采取两种信号的互相关函数进行分析。仿真结果证实提出的基于小波变换与相关性分析的误差辨识方法有效。
1 小波变换原理及检测信号分解
1.1 Daubechies小波变换原理
小波变换是一种信号的时间、尺度(时间—频率)的分析方法,具有多分辨分析的特点,且在时、频域都具有表征信号局部特征的能力,是一种窗口大小固定不变但其形状可改变的时频局部化分析方法。它的实质是将信号向一系列小波基上进行投影,包括离散小波变换和连续小波变换[11]。离散小波变换理论主要建立在多尺度分析或滤波器的基础上,相对而言,连续小波变换在对信号细微变化的探测时更灵敏。不同类型的小波如Daubechies小波、Haar小波、样条小波和Mexican Hat小波等都已用于信号处理的研究中。值得注意的是,具有紧支集的正交小波无论在理论上还是在应用中都有特别重要的意义,尤其在数字信号的小波分解过程中可以提供有限长的更实际更具体的数字滤波器,因而使得紧支集正交小波更具重要性。由于Mexican Hat小波不具正交性、样条小波支集非紧,Haar小波虽支集紧且正交,但非连续导致频域局部性差,因此导致它们在许多实际应用中受到限制。而具有不同紧支集的Daubechies小波由于其支集紧、正交、又具有一定的光滑性[12],自提出后就受到广泛重视。
法国学者 Daubechies(1988)[12]对尺度为2整幂条件下的小波变换进行了较深入的研究,提出一类具有以下特点的Daubechies小波:

(2)在频域上y(w)在w=0处有L阶零点。
(3)y(t)和它的整数位移正交归一,即∫ψ(t)ψ(t-k)dt=δk。
(4)小波函数y(t)可以由尺度函数f(t)求出。f(t)在时域上的紧支集为:t∈[0,N],N=2L-1,且有:

(5)y(t)是f(2t)的位移加权和
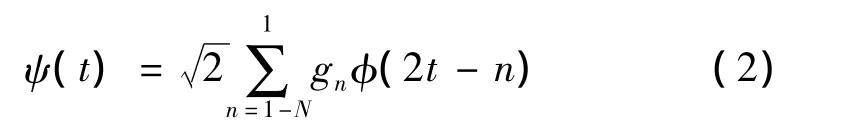
可见,y(t)在时域上的紧支集为:t∈[1-L,L]。
(6)尺度函数是低通函数,其滤波器系数为hn(n=1,1…,N),对应于小波函数y(t)的高通滤波器系数gn为
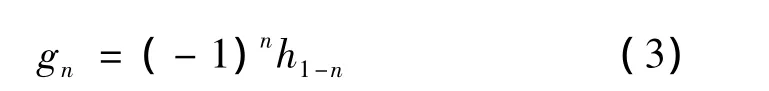
在文献[12]中,Daubechies给出了L从2到10的9种滤波器系数。根据滤波器系数为hn和gn,不难由方程(1)和(2)求出Daubechies尺度函数和小波函数。
在尺度空间Vj,函数f(x)的大尺度逼近部分可以表示为
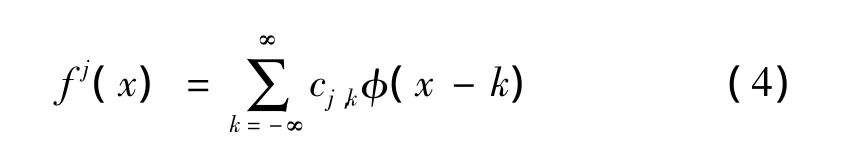
同理,在小波空间Wj,函数f(x)的细节部分可以表示为

式 中:j为是任意尺度;cj,k为尺度展开系数;dj,k为小波
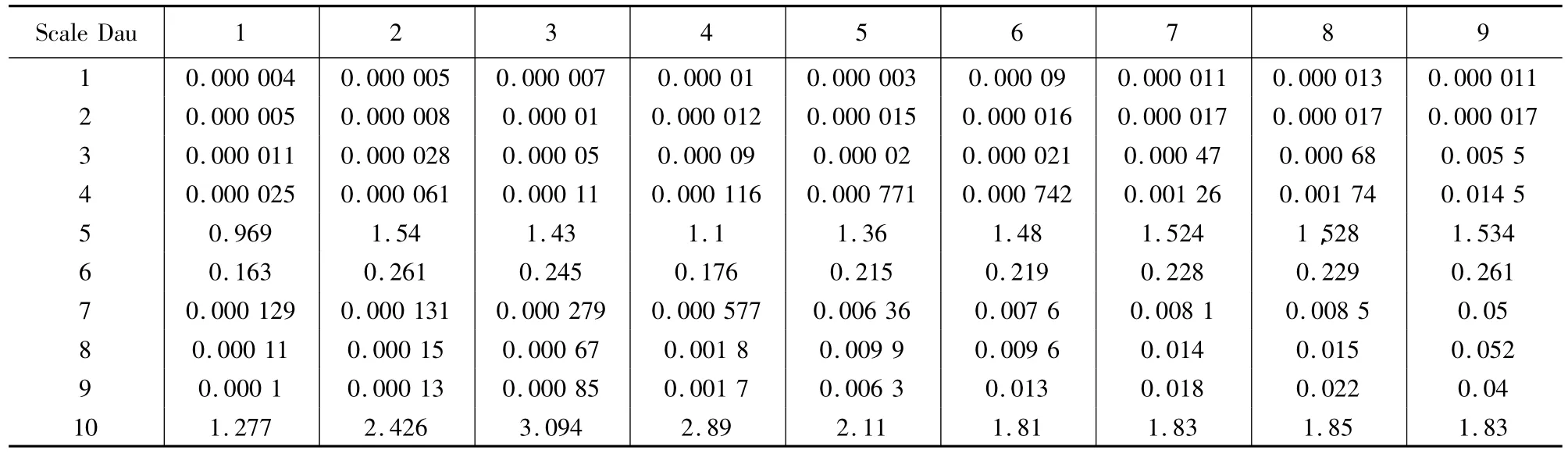
表1 不同尺度下不同小波的分解误差
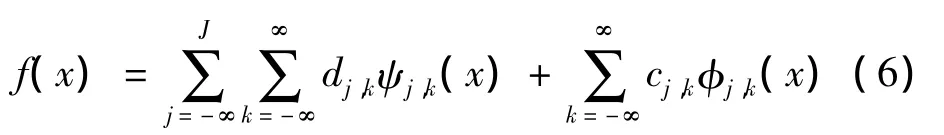
根据Mallat快速算法[13],对任意函数f(x)∈V0函数空间,可将其分解为细节部分W1和大尺度逼近部分V1,然后将大尺度部分进一步分解。如此重复就可得到任意尺度或分辨率上的逼近部分和细节部分。设尺度0上的尺度系数为c0,k,可按如下分解公式计算任意尺度下的尺度系数和小波系数:
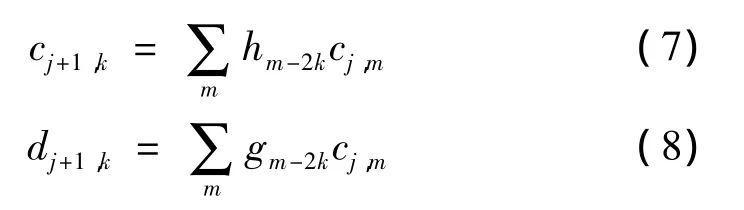
根据分解的尺度系数和小波系数,通过设定除某一尺度下的小波系数或尺度系数不为0而其他尺度下的小波系数或尺度系数为0,然后按式(6)重构信号到0尺度,便得到在设定尺度下的根据原始信号分解得到的细节信号或概貌信号。
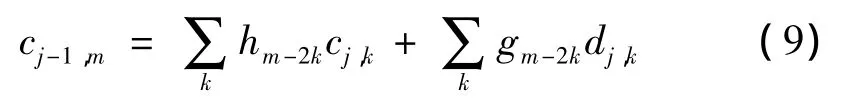
式(7)~(9)中的滤波器系数hn、gn可由不同紧支集的Daubechies小波滤波器给出[12]。根据式(6),可见,原始信号x(t)(t=1,2,…NT)通过 Daubechies小波Mallat分解与重构算法后便为展开系数。
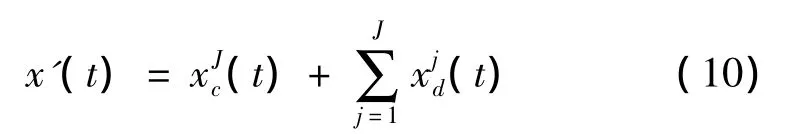
若将f(x)∈L2(R)按空间组合Wj⊕Vj展开(数学异或符号,两个值相异结果为真),则:
设原始信号不同紧支集Daubechies小波分解的误差En为
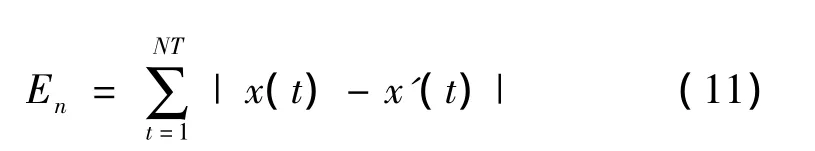
可见不同的DauN小波将给出不同的滤波器系数hn,gn,从而给出不同分解的误差为En。
将面形检测信号代入公式(6)进行Daubechies小波变换,得到尺度和小波系数,同时,也可以得到不同的Daubechies小波分解误差。表1给出了根据公式(11)得出的不同尺度上不同小波分解的误差。它表明,紧支集为[0,1]的Dau1小波具有最小分解误差,紧支集为[-9,10]的Dau10小波引起的分解误差最大,紧支集为[-4,5]的Dau5小波分解误差第二大。对于同一类型小波,基本趋势是分解尺度越大,分解误差越大,比如 Dau(2-4),Dau(7-9)。Dau10,Dau5和Dau6小波分解误差相对比较大,在尺度2到4有最大误差。
1.2 工件加工及其面形检测
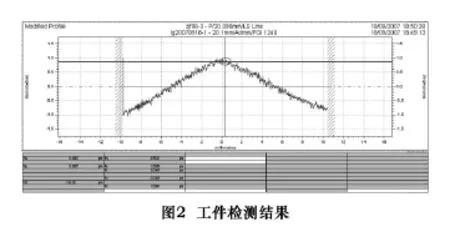
本文用两轴立式超精密数控机床加工一直径为10 mm的平面,工件材料为LY16,主轴转速为110 r/min,背吃刀量为15 μm,进给量为2 mm/min。机床结构如图1所示,包含X向导轨和Z向导轨。利用PGI1240轮廓仪对加工工件面形精度进行检测,检测结果如图2所示。

对于加工工件的检测信号,是含有多个误差综合作用的信号,这些信号相互作用、相互干扰,给误差源信号的辨识造成了很大困难。每一种误差源都对应特定的特征和频率成分,需要通过适当的信号处理方法将单一频率成分和特征分离出来,从而找出特定误差源。如何从混合误差信号中辨识出主要误差源信号,是机床加工精度提高的关键。
1.3 基于小波变换的工件检测信号分解
利用Db1小波将检测的工件信号分解到不同的频段上,然后在不同的频段范围内对检测信号进行分析,找出需要的频段进行重构,再进一步分析信号突出部分特征。首先,利用Db1小波把检测信号进行5层分解,小波分解结果如图3所示。

加工工件的检测结果是各个频段的误差源综合,因此检测结果x(t)可以表示为
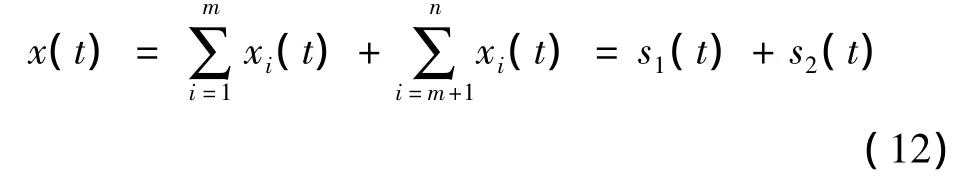
第一部分s1(t)由各低频信号成分叠加构成:
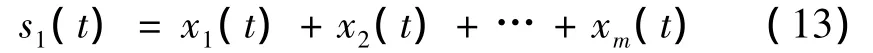
第二部分为各高频信号的叠加即原始信号和第一部分信号分量的差信号:
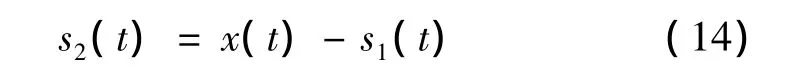
把x(t)代入公式(6)中进行小波变换,提取有用的信息得到不同尺度上的小波系数,小波系数代表不同频段误差源的误差形状,并且分解出低频部分信号s1(t)和高频部分信号s2(t),不同的信号对应不同的频率段。对分解出的每个频段的信号与机床误差源对映,所应用方法为相关性分析,根据相关函数值推导出对加工结果影响大的机床误差源。
2 相关性分析原理
相关分析法主要是用来分析某些因素之间是否关联,关联程度多少的方法[14]。机床的加工精度是对误差源的间接反映。加工结果中包含了多少误差源,与每个原始误差源的相关联的程度用相关函数来进行分析。相关函数分为自相关函数和互相关函数。
2.1 自相关函数
自相关函数Rxx(τ)是度量一个变化量或随机过程在t和t-τ两个时刻线性相关的统计参量,它是t和t-τ两点的时间间隔τ的函数,定义为
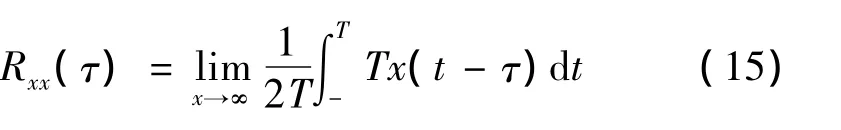
分析表明,自相关函数具有下列性质:
(1)Rxx(τ)=Rxx(-τ),即Rxx(τ)为τ 的偶函数。
(2)Rxx(τ)在原点τ=0处最大。并且Rxx(0)代表x(t)变化量的平均功率。
(3)若变化量x(t)不包含周期性分量,则Rxx(τ)代表x(t)变化量的平均功率。
(4)若变化量x(t)为规则函数,即包含有周期性信号分量,则自相关函数Rxx(τ)也将包含有周期性信号分量。
2.2 互相关函数
互相关函数Rxy(τ)是度量两个随机过程x(t),y(t)间的相关性函数,定义为
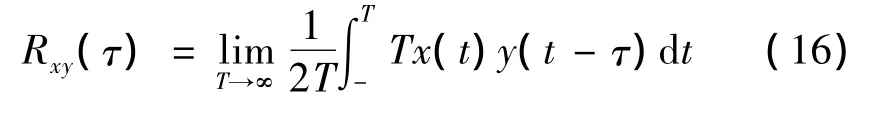
式中τ为所考虑时间轴上的时间间隔。如果两个随机过程互相完全没有关系,则其互相关函数将为一个常数,并等于两个变化量平均值的乘积,若其中一个变化量平均值为零,则两个变化量互相关函数Rxy(τ)将处处为零,即完全独立不相关。
需要特别指出的是:在相关性分析中必须有一个定量的指标来度量变量间的相关性强弱。数学上用相关系数来表示两个变量之间线形相关的强弱程度:
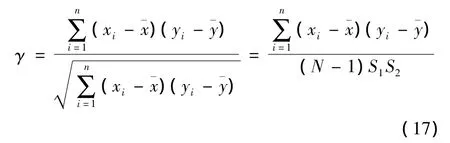
式中S1、S2分别代表第一个变量的标准偏差和第二个变量的标准偏差。
3 基于试验的误差辨识及讨论
根据对本机床导轨误差的分析[15],这里对导轨误差与检测结果做相关性分析,导轨误差的仿真数据与加工工件的检测结果为2个不同过程信号。这里假设检测过程的信号为x(t)=x1(t)+x2(t),其中x1(t)是由db1小波分解的检测信号中的低频信号,x2(t)为相应的高频信号;导轨误差的仿真过程信号设为y(t)=y1(t)+y2(t),其中y1(t)是导轨垂直度误差仿真信号,y2(t)是导轨的直线度误差仿真信号。从而根据公式(17)可以得到相关系数γxym和γx1ym为
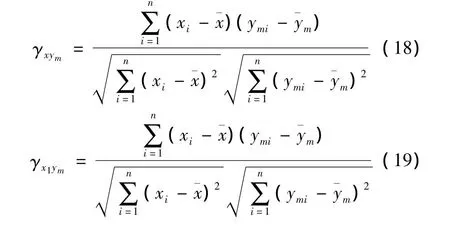
其中m=1、2。公式(18)中的γxym代表检测信号x(t)和仿真信号y(t),包括y1(t)和y2(t)之间的相关系数,公式(19)中的γx1ym代表检测信号中的低频信号和仿真信号y(t)之间的相关系数。
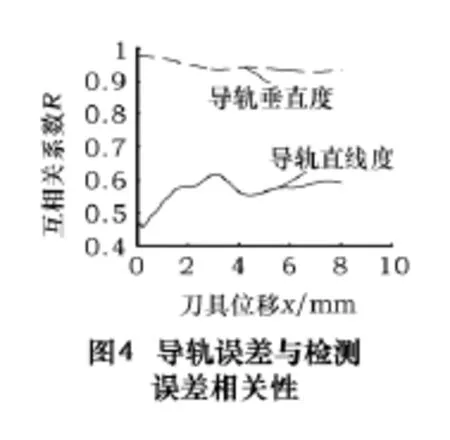
图4给出了小波变换后的检测信号与导轨误差仿真信号的相关函数曲线。从图中的相关性分析结果来看,检测信号x(t)与导轨垂直度信号y1(t)相关系数γxy1的范围为0.6~0.83,检测信号x(t)与导轨直线度信号y2(t)的相关系数γxy2的范围为0.45~0.6,这个值范围比垂直度相关系数范围小。所以我们可以得出,导轨误差中,对加工精度影响较大的是导轨的垂直度误差,导轨的直线度误差影响较小。其中起主要影响作用的是导轨垂直度误差。
4 结语
基于小波变换与工件面形误差的机床误差分析方法,为机床误差源的分析与辨识提供了一种有效辨识误差途径。其基本过程如下:
(1)利用Daubechies小波变换模型,把检测的工件面形结果分解为高频信号部分和低频信号部分,从而提取出高频信号特征和低频信号特征。
(2)针对低频信号部分,在时域内与低频误差源仿真结果作相关性分析,根据相关函数值确定对加工结果影响大的误差源。
最后的仿真结果证实了提出的小波变换与相关性分析这种辨识方法的正确性与有效性。
[1]商鹏,阮宏慧,张大卫.基于球杆仪的三轴数控机床热误差检测方法[J].天津大学学报,2006,39(11):1336-1340.
[2]李国纯,李书富,聂恒敬.机械量仪与光学量仪[M].北京:中国计量出版社,1987.
[3]刘建亭,沈云波,李济顺.机床误差正交光栅检测及补偿的研究[J].组合机床与自动化加工技术,2004,4:76 -77.
[4]Cheng C F,Lee W B.A Muti-spectrum analysis of surface roughness formation in ultra - precision turning[J].Precision Engineering,2002(24):77-87.
[5]Dong-Sik Kim,In-Cheol Chang,Seung-Woo Kim.Microscopic topographical analysis of tool vibration effects on diamond turned surfaces[J].Precision Engineering,2002,26:168 -174.
[6]何正嘉,孟庆丰,赵纪元.非平稳机械动态信号的时频分析[J].动态分析与测试技术,1992(3):5-11.
[7]Rodgers J L,Nicewander W A.Thirteen ways to look at the correlation coefficient[J].The American Statician,1988,42:59 -66.
[8]Andren L,Hakansson L,Brandt A,et al.Identification of motion of cutting tool vibration in a continuous boring operation-correlation to structural properties[J].Mechanical Systems and Signal Processing,2004,18:903 -927.
[9]Rehorn Adam G,Sejdic Ervin,Jiang Jin.Fault diagnosis in machine tools using selective regional correlation[J].Mechanical Systems and Signal Processing,2006,20:1221-1238.
[10]Suryannarayana Chandaka,Amitava Chatterjee,Sugata Munshi.Cross-correlation aided support vector machine classifier for classification of eeg signals[J].Expert Systems with Applications,2009,36:1329 -1336.
[11]孙延奎.小波分析及其应用[M].北京:机械工业出版社,2005.
[12]I Daubechies.Orthonormal bases of compactly supported wavelets,Commun.Pure Appl.Math,1988,41(7):909 -996.
[13]Mallat S,A theory for multiresolution signal decomposition:the wavelet representation,IEEE Trans Pattern Anal Mach Intell,1989,11(7):674-693.
[14]冯之敬.机械制造工程原理[M].北京:清华大学出版社,1999.
[15]Chen D J,Zhang F H,Dong S,et al.Identification and analysis of the guideway error based on the cross-correlation analysis in machine tools[J].Proceeding of the euspen Internaltioinal Conference.San Sebastian,2009(6):435-438.

