积分奇点问题浅析
吕淑婷
(北方民族大学信息与计算科学学院,银川750021)
积分奇点问题浅析
吕淑婷
(北方民族大学信息与计算科学学院,银川750021)
文章讨论了积分计算出现奇点时,通过巧妙的添加新的辅助线(面),挖去奇点构造新的复连通区域的求积分方法,本质上是对相应的公式做了推广,从而使对各类积分公式的运用有更深层次的掌握,加强了对各类积分联系的理解.
积分;连续;奇点
在求积分时,只要函数在积分区间或区域满足连续或偏导数连续,就可以利用相应的积分公式直接求积分,但是如果有奇点时,相应的公式就不能直接利用(很多初学者对此问题理解不够深透,直接利用从而导致积分错误).此时根据一元函数与多元函数积分的关联,巧妙而简洁的给出了处理积分区间或区域内有奇点时的积分问题的方法.文献[1]讨论积分区域边界上含奇点的Green公式应用,文献[2]讨论运用高斯公式应注意的一个偏导数连续与否的问题,本文讨论一元函数与多元函数积分区间(区域)内部出现奇点时,采取挖去奇点的处理方法,使新的区间(区域)内函数可积,是对文献[1]的总结和推广.以下从三个方面加以讨论:
1 牛顿—莱布尼茨积分公式运用时的奇点问题
定理1 如果函数F(x)是连续函数f(x)在区间[a,b]上的一个原函数,则F(a).
表明:一个连续函数f(x)在区间[a,b]上的定积分等于它的任意原函数在区间[a,b]上的增量.公式中要求f(x)必须连续,如果不满足条件呢?如积分:,知x=0为瑕(奇)点,如果忽略了x=0为被积函数的奇点,就会得到如下错误的结果:那么怎样处理此积分呢,方法是挖去奇点,具体如下:
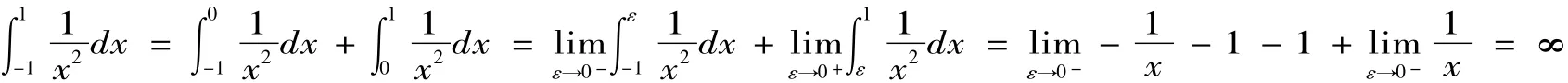
特别是,若被积函数在积分区间有多个奇点时,采用的方法是逐个挖去,即在[a,b]内构造若干个互不包含互不相交小区间,在[a,b]内挖去小区间的区间上,仿上题运用牛顿-莱布尼茨公式公式可求得相应积分.
2 格林公式运用时的奇点问题
定理2 设区域D是由分段光滑的曲线L围成,函数P(x,y)及Q(x,y)在D上具有一阶连续偏导,则有:,其中L是D的取正向的边界曲线.
若函数P(x,y)及Q(x,y)在D上不满足具有一阶连续偏导的条件,即若P(x,y)及Q(x,y)在D上有奇点时,如:计算曲线积分为一条无重点分段光滑不过原点的连续闭曲线,L的方向为逆时针方向,L围成的区域D含原点.

其中l的方向取逆时针方向,于是
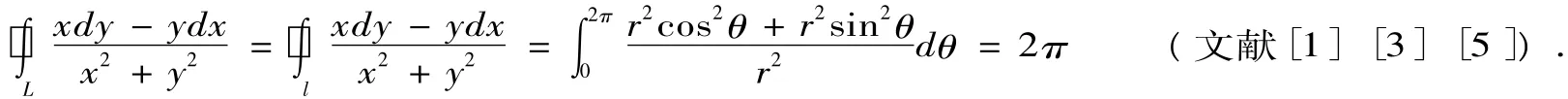
特别是,若被积函数在积分区域有多个奇点时,采用的方法是逐个挖去,即在D内构造若干个互不包含互不相交小圆,在D内挖去小圆域的区域,仿上题运用格林公式可求得相应积分.
3 高斯公式运用时的奇点问题
定理3 设区域Ω是由分片光滑的闭曲面∑所围成,函数P(x,y,z),Q(x,y,z),R(x,y,z)在Ω上具有一阶连续偏导,则有

这里∑是Ω的整个边界曲面的外侧.
同样,定理要求P(x,y,z),Q(x,y,z),R(x,y,z)在Ω上具有一阶连续偏导,若条件不满足,即P(x,y, z),Q(x,y,z),R(x,y,z)在Ω中有奇点时,如:求曲面积分,其中∑为曲面的上侧.若不注意(0,0,0)是奇点,直接利用高斯公式,导致错误结果(许多高等数学习题解书籍上就是犯了这样的错误).正确的处理方法也是将奇点挖去,设,其中
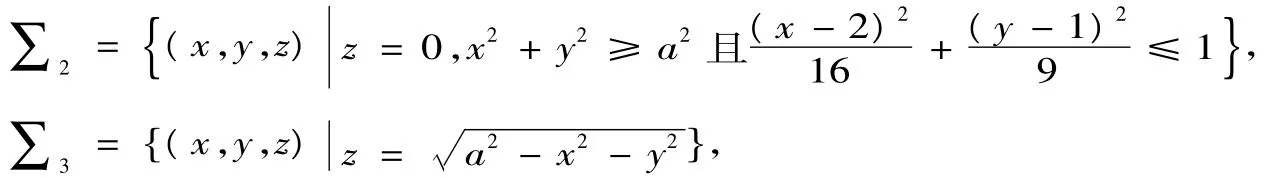
取下侧,a为足够小的常数,使上半球面∑3与积分曲面∑不相交
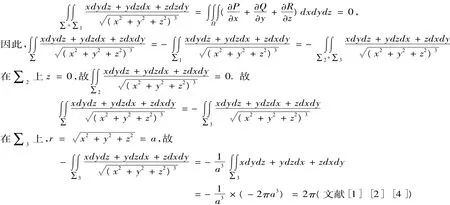
特别是,若被积函数在积分区域有多个奇点时,采用的方法是逐个挖去,即在Ω内构造若干个互不包含互不相交小球,在Ω内挖去小球域的区域,仿上题运用高斯公式可求得相应积分.
综上可以看出,当出现奇点时,有效的处理方法是添加新的辅助线(面),挖去奇点将原区域变为复连通区域从而运用相应的公式.
[1]唐玉华.积分区域边界上含奇点的Green公式应用[J].重庆工商大学学报,2008,25(5):464-466.
[2]李菊.运用高斯公式应注意的一个问题[J].高等数学研究,2000,(3):13-14.
[3]同济大学应用数学教研室.高等数学[M].北京:高等教育出版社,2002.
[4]邓东皋,尹晓玲.数学分析简明教程[M].北京:高等教育出版社,2002.44-59,292-358.
[5]华东师范大学数学系.数学分析(下)[M].北京:高等教育出版社,2001.272-292.
[责任编辑 舒尚奇]
Abstract:This paper discusses the integral calculation when the singularity point occurs.This integrationmethod is based on adding a new Auxiliary line(surface)and digging singularity point to construct a new complex connected region.In essence,this method is the promotion for corresponding formula.Hence,we further grasp the use of various types of integral formulas and strengthen the understanding of the relation of various integrations.
Key words:integration;continuous;singularity point
Analysis of Integration of the Singular Point
LV Shu-ting
(School of Information and Computation Science,North University for Nationalities,Yinchuan 750021,China)
O13
A
1009—5128(2011)02—0026—03
2010—10—26
北方民族大学科学研究项目(2009Y031)
吕淑婷(1976—),女,陕西宝鸡人,北方民族大学讲师,硕士.研究方向:随机微分方程数值解.

