基于模糊综合评判的数控车床故障分析*
申桂香 高文礼 张英芝 何 宇 刘 葳
(①吉林大学机械科学与工程学院,吉林长春 130025;②长春理工大学生命科学技术学院,吉林长春 130022)
数控机床的故障机理与表现形式复杂多样,大部分故障最终都反应在机床不能正常加工或加工件出现质量问题,致使在评估数控机床的故障模式影响及危害度时,存在很大的模糊性。对机床进行故障分析找出薄弱环节是解决这一问题的有效方法,故障模式、影响及危害性分析(Failure mode,effects and criticality analysis,FMECA)是常用的故障分析方法[1],然而根据国标草案确定的故障模式影响数值不能充分描述数控机床各故障模式造成零部件损伤的概率。本文充分考虑机床发生故障的随机性与模糊性,采用基于模糊综合评判的故障模式分析方法,引入圆形隶属度函数,对某系列国产数控车床故障模式影响进行模糊计算得出模糊评判矩阵,进而计算各子系统危害度排序,找出危害度较高的子系统,提高数控机床故障分析的准确性。
1 故障模式的不确定性
数控机床的不确定性通常可分为4类:随机不确定性、模糊性、灰色性不确定性和未确知不确定性[2]。模糊性和模糊现象在数控机床的可靠性方面是客观存在的。对于数控机床故障模式的模糊性,大致由数据的模糊性、数控机床硬件模糊性以及人员模糊性组成。数据模糊性是在获取数据过程中遗漏数据、分辨率、机床本体结构复杂等引起的;硬件模糊性是由设备运行故障现象与故障部位没有明确的对应关系、机床状态的好坏没有明显界限以及人们对故障现象的观察本身也是不明确的;人员模糊性是由人的独特性带来的不确定性。
2 危害度的模糊综合评判
对数控机床进行危害度的模糊综合评判主要有3个因素:故障率λ、故障模式频率比α和故障影响β。其中β是指故障对整机的影响,用固定量值来描述这一参数是不够准确的。因此本文选择一个模糊区间来表示β,以故障影响为因素集建立相应的评语集,选取模糊隶属函数,建立故障影响模糊评判集,根据影响度计算公式得到近似于精确数控机床的一个综合评判结论。
2.1 定性评估指标的归一化
针对数控机床FMECA评价特性和评价指标的选取特点,通过参考模糊综合评判方法在其他领域的应用实例,本文将评语集定为{很小、小、一般、大、很大},共5个等级,把经典集合的绝对隶属关系扩展为各种不同的隶属程度[3]。具体说明见表1。
在机床系统危害度的评估上,当定性指标采用{很小、小、一般、大、很大}的方式描述时,可根据它们的次序粗略地分别分配一个区间来实现结果的量化,此处使用0~5的区间与之对应。

表1 评语集
2.2 模糊函数的选取
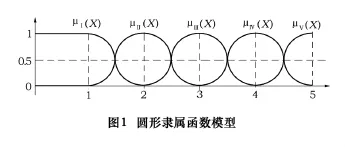
判断隶属函数是否符合实际情况,主要看它是否正确地反映了元素隶属集合到不属于集合这一变化过程的整体特性,而不在于单个元素的隶属度数值如何选取。根据构造隶属函数的基本原则,在任何一个模糊等级范围的中间区域既要保持一定的隶属度的稳定性,又要体现该区域内的细微差别,即均可认为中点处可以定义为绝对地属于该等级,即隶属度定为1,随着与该中点的距离变大,属于该等级的隶属度就变小,而且其变化率应该是由小变大(变化率最小值为0),当到达2个连续等级中间点时,这种变化率应该是最大的,且此时2个隶属度相等,都为0.5,过了该中间点变化率则又是由大变小,直到为0。为此,下面在利用模糊综合评判法评价机床危害度时,对参数βij的模糊采用了符合上述要求的圆形隶属函数模型[4],并且给定性指标各等级赋边界值。按照以上方法,此处相应于等级很小(Ⅰ)、小(Ⅱ)、一般(Ⅲ)、大(Ⅳ)、很大(Ⅴ)对定性指标赋予数值 1、2、3、4、5 的边界值,函数形式如图1所示。
横轴表示定性指标,此处为数控机床故障影响参数的区间变换值,纵轴表示隶属度,范围由0到1。以定性指标2为例,当危害度值归一化值处于2时认为绝对属于这个等级;当危害度归一化值小于1或者大于3时,由于此时变化率极低,可认为此时完全不隶属于这个等级;当大于1而小于2且逐渐变大时,其变化率也应该是由小变大,隶属度随之由小变大;当大于2而小于3时,其隶属度应由大变小。
2.3 β参数数据模糊
以某型号国产数控立式车床为研究对象,根据可靠性改进设计的需要,将该型号数控立车分成15个子系统或部件,分别是主传动系统、工作台、刀架、X轴进给系统、Z轴进给系统、CNC系统、伺服控制单元、冷却系统、电源、装卡附件、液压系统、气动系统、润滑系统、电气系统和防护装置。
零部件i以故障模式j发生故障致使该零部件发生故障的危害度CRij,其计算公式为

零部件i对整机的危害度为

将式(1)代入式(2)得
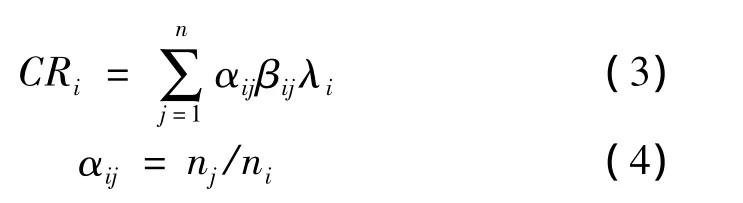
式中:n为零部件i出现的故障模式的种类数;αij为零部件i以故障模式j而引起该零部件发生故障的故障模式概率;nj为零部件i第j种故障模式出现的次数;ni为零部件i全部故障模式发生的总次数;βij为零部件i以故障模式j发生故障造成该零部件损伤的概率,国标草案将此称为丧失功能的条件概率,βij=1表示该件肯定发生损伤,βij=0.5表示该件可能发生损伤,βij=0.1表示该件很少发生损伤,βij=0表示该件无影响;λi为零部件i的基本故障率,是通过现场实验得到的平均故障率i,其计算公式为

式中:Ni为零部件i在规定时间内的故障总次数;∑t为零部件i在规定时间内累积工作时间,15台数控立车的累积工作时间为19 252 h(双班制)。
本文以主传动系统为例,该系统在考核期间共发生18次故障,由式(5)计算得:=0.000 935。
主传动系统的FMECA数据计算结果见表2。将βij(零部件i以故障模式j发生故障造成该零部件损伤的概率)根据隶属度函数要求进行区间变换后(见表3第4列),通过式(6)得到该参数的模糊评判矩阵β,计算出每个故障模式对应的近似精确危害度。由于数控立车各个子系统的故障模式个数参差不齐,故先将具有一个故障模式且故障率较低的子系统定义为“其他”子系统(本文将冷却系统、电源以及气动系统转移到“其他”)。
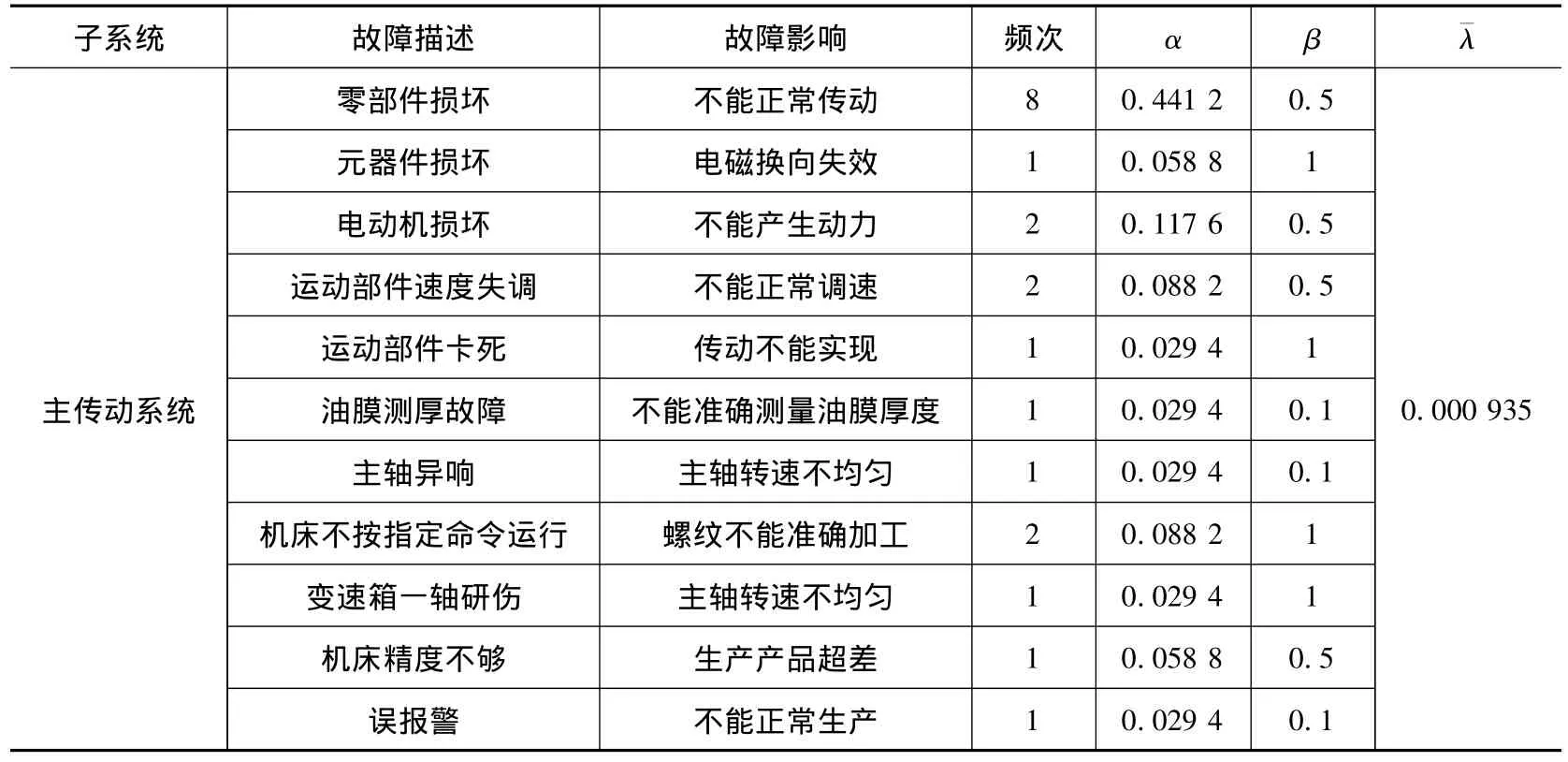
表2 主传动系统FMECA表

表3 故障影响参数的变换数据及隶属度
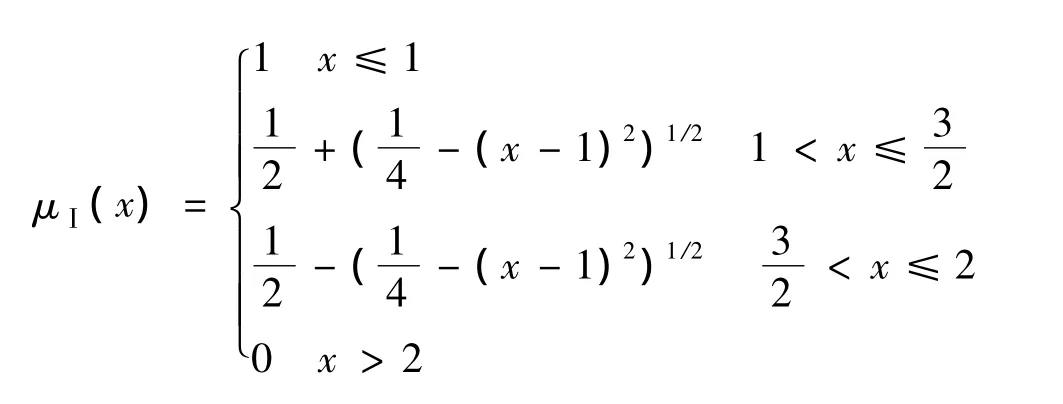

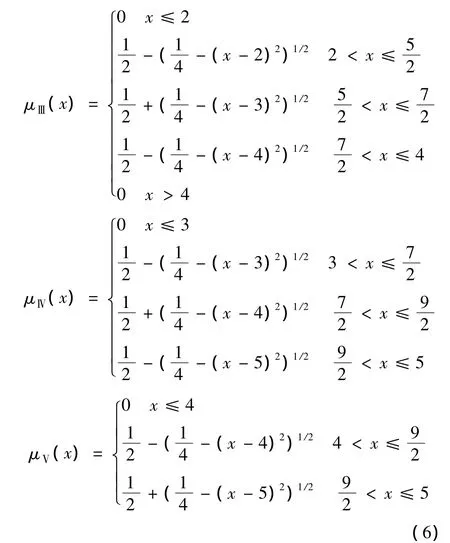
2.4 综合评判
结合数控车床故障模式的特点[5-6],既有的故障模式很多,这样势必导致权重系数都比较小,与隶属度值相比,不在同一个数量级上,所以在运算将各子系统模糊后的危害度在各个隶属区间的比重乘以区间值再相加。
以主传动系统为例对其进行危害度模糊综合评判,评判矩阵为

主传动系统各故障模式的模糊危害度评价结果为

主传动系统的危害度模糊综合评判结果由加权平均值得到

由于模糊后的危害度值不分布在评估指标内,因此在不影响危害度排序的基础上将其再进行区间变换(同时放大1 000倍),其他子系统及危害度评价值排序见表4。从表4中可以看出在各个子系统中,主传动系统与数控刀架的危害度接近中等,隶属于“一般”,应该引起相当的重视。我们对各个子系统按照模糊综合处理分析后,发现其排序和按照频率的排序并不一致,有些子系统的故障模式发生机会比较大但频率并不高,这也说明了如果只是单纯按照发生故障频率的多少来决定每种故障模式的发生具有片面性,其考虑的因素是不全面的,因此应用基于模糊综合分析的方法是必要的。

表4 各子系统危害度评价及其排序
3 结语
将模糊综合评价法应用于数控立车的可靠性分析,充分考虑了主客观因素以及各故障模式的不确定关系,使用了圆形隶属函数这一更接近数控车床隶属度定义的工具,对数控车床故障情况进行模糊综合评价,得出数控刀架和主传动系统的危害度最高。给出准确的评判等级,对危害度高的子系统必须要引起足够重视,要从设计、制造和使用等过程中尽量消除或减少该子系统所对应的故障模式,对其关键部位设置保护、检测和报警装置,以求能达到提高数控车床可靠性的目的,为实现数控车床整机的可靠性设计提供基础数据,为实施故障纠正及开发可靠性增长技术提供依据。
[1]张英芝.基于模糊与灰色理论的数控车床可靠性分析[D].长春:吉林大学,2005.
[2]胡圣武,张光胜.论GIS的模糊性[J].测绘科学技术学报,2007,24(3):164-166.
[3]薛玉霞.基于模糊逻辑的数控机床故障综合分析方法的研究[D].长春:吉林大学,2005.
[4]章熙海.模糊综合评判在网络安全评价中的应用研究[D].南京:南京理工大学,2006.
[5]许崇文.基于FMEA和重要度分析的数控车床可靠性改进设计[D].长春:吉林大学,2008.
[6]于捷,于双.数控车床 FMECA 分析[J].长春大学学报,2000,10(5):4-6.

