基于RBF神经网络的主轴热变形实时测量与研究*
伍良生 翟少剑 周大帅 马建峰
(北京工业大学机械工程与应用电子技术学院,北京100124)
机床工作时,在内、外热源的作用下,主轴系统的各个部分(如滚珠丝杠、轴承、定子、切削过程以及冷却和润滑液等)都会产生不同程度的温升。升温后,主轴和机床其他部件的空间相对位置和尺寸都将与温升前不同,形成不同的温度场,进而产生不同程度的热变形,导致加工精度误差[1-3]。据统计,主轴单元的热变形已经成为影响加工精度的主要因素,已达到工件总加工误差的40% ~70%[4-6]。所以,要提高机床的加工精度,就必须采取有效的措施减小热误差。误差补偿是最常用有效的方法之一,经济性也好,既可应用于新机床,也可用于旧机床的改造。但热误差补偿的关键是尽可能准确地进行热误差建模,即建立机床热误差和温度之间的关系,从而在实时补偿过程中用机床温度值来预报热误差。
国内外许多学者都对热误差进行了大量的有益研究,大多是采用有限元的方法建立温度场模型[7]。但由于主轴是个复杂系统,各零件之间的传热系数及传热方式不易具体确定,这些非线性因素及其交互作用的影响,致使很难精确地确定其热变形误差[8-10]。神经网络理论是利用工程技术手段模拟人脑神经网络结构和功能的一种非线性动力学系统,并已成功运用到热误差建模中。本文运用径向基函数(Radial Basis Function,RBF)神经网络对机床进行热误差建模,首次采用美国API公司的主轴热变形分析系统,对主轴热变形误差进行实时试验研究,为主轴的精度提高和实时精度补偿提供了重要的数据依据。
1 主轴热误差模型及测量系统
1.1 RBF网络热误差模型
常用的热误差模型有多元线性回归分析模型法、神经网络模型法、综合最小二乘建模法、正交试验设计建模法和递推建模法等等[11],所有这些热误差模型,都为误差预测建模技术注入了新的活力,特别是神经网络理论的运用,使对复杂系统的建模成为可能。本文运用RBF神经网络的方法对机床热误差进行建模,是因为它具有模型拟合性好、补偿能力强、建模时间短且对传感器的布置具有一定的鲁棒性。
人工神经网络模型由一定数量的神经元相互连接组成的1个非线性系统,每个神经元具有单一输出,并且与其它神经元连接,但它们之间又存在着多种连接方法,每2个神经元之间存在着特定的连接权系数。根据机床温度测量的特点和对输入输出的要求,选择局部逼近的神经网络[12]。
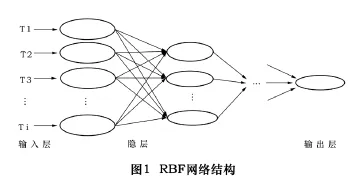
该网络由3层节点组成,即输入层、中间层(隐层)和输出层,如图1所示。输入层节点只是传递输入信号到中间层,对于温度测量模型来说就是各测量点的温度;中间层由像高斯核函数那样的辐射状函数构成;输出层是简单的线性函数,对于温度测量模型来说就是5自由度主轴的温度误差。隐层中的作用函数(核函数)对输入信号将在局部产生响应,即当输入信号靠近核函数的中央范围时,隐层节点将产生较大的输出。核函数中最常用的是高斯核函数,如式(1)所示:
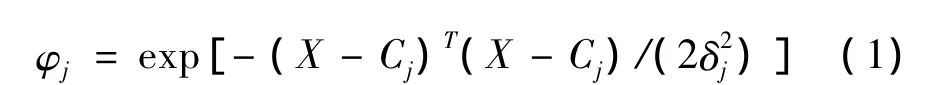
式中:φj是第 j个隐层节点的输出,j=1,2…,nh;X=(x1,x2,…,xn)T是输入样本,即测量点的温度值,Cj是高斯函数的中心值,δj是标准化常数,nh是隐层节点数。该神经网络输出为隐层节点输出线性组合,即:
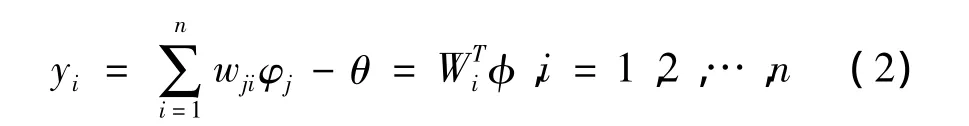
1.2 5自由度主轴热误差测量系统
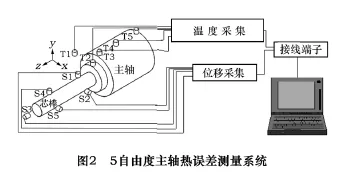
主轴的旋转是1个复杂的运动,它包括6个自由(6 DOF)误差运动,即:2个径向运动误差,1个轴向运动误差,2个转角运动误差和1个绕测量轴旋转的滚摆角。从机床测量实际角度出发,滚摆角运动可以忽略(即第6个自由度主轴的公转)。因此,本文采用ASME(USA)主轴测量评价系统——5自由度主轴温度误差测量系统,对主轴进行实时测量。系统结构如图2所示,该装置由1根心棒和5个电容位移传感器、5个热电偶温度传感器及控制盒等硬件组成,经USB接口和电脑测量软件相连。图2中S2、S5为X轴方向热漂移变形量,S1、S4为Y轴方向热漂移变形量,S3为Z轴方向热漂移变形量。
2 主轴热变形分析系统的实时测量与研究
2.1 测试设备的安装与调整
API主轴热变形分析系统(THERM-500,由美国自动精密工程公司提供)由5个热电偶传感器、5个电容位移传感器、控制接线盒通过USB接口和PC机相连,测量范围 0 ~0.7 mm,分辨率 0.1 μm,精确度 0.5 μm。它的精妙设计在于能够适应厂房现场和各种生产环境的测量,并且为了发挥最大的测量性能,测量精度也是经激光校准。此系统配有完全的交互式的软件使用户能够很容易地进行界面操作和数据分析。根据ANSI/ASME中主轴热变形测量中的相关规定,在主轴的发热源处轴向安装T1~T4热电偶传感器(热变形实时补偿系统中有T1~T20个热电偶传感器)和环境温度参考热电偶传感器,在主轴上安装标准芯棒,用磁力座安装测试夹具,如图3所示,调整固定测试夹具与主轴端面的距离为150 mm。
打开API的主轴热变形分析系统和控制接线盒的电源,显示主轴热变形分析系统如图4所示。手工转动主轴,调整5个高性能非接触位移传感器和主轴之间的间隙距离,使波动范围在图4中参考线附近后固定,左侧是所用热电偶传感器所测量的温度值和位移传感器实时测量值。


测试过程分3种测试工况:①恒速连续运转模式,在这种工况下,主轴从常态启动,以某一恒速(如1 000 r/min)连续运转;②渐进式连续运转,在这个工况下,主轴转速渐进式递增(或递减),各速度转动时间相隔 10 min,如 0 r/min、1 000 r/min、2 000 r/min、3 000 r/min,然后从 3 000 r/min、2 000 r/min、1 000 r/min、0 r/min递减;③随机式连续运转。
2.2 主轴系统的误差采集和分析
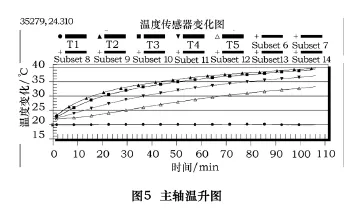
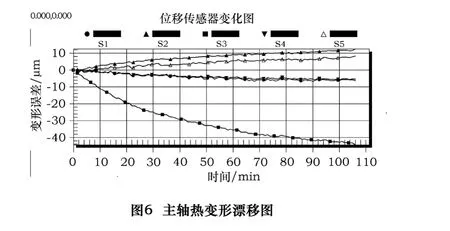
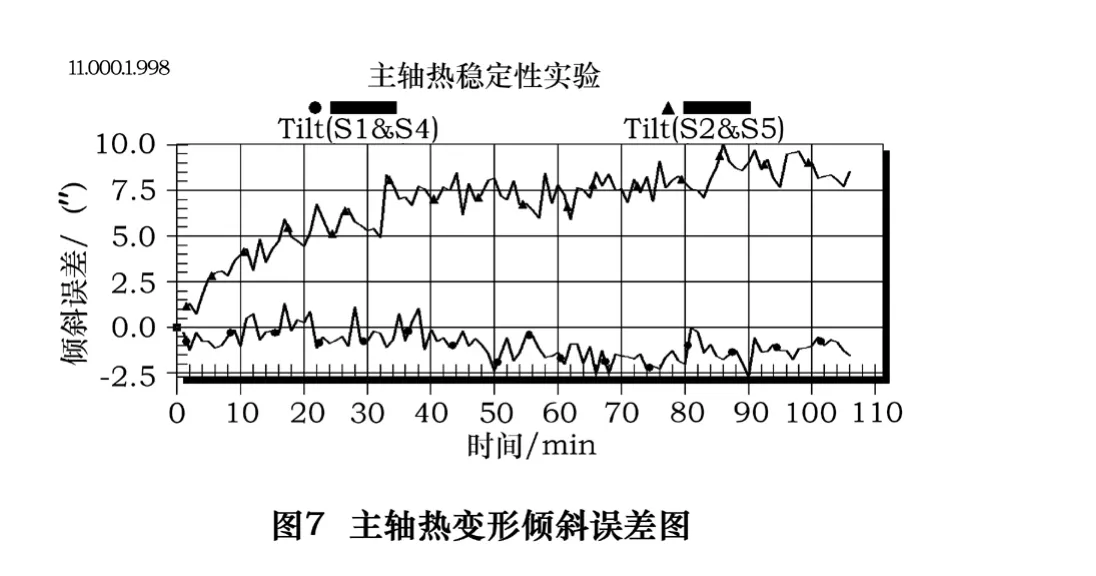
依据上述基本要求,开启主轴和测试系统以上面所述的某一工况进行测试。本文以第一种工况转速为1 000 r/min进行测试(取前120 min,实际各工况连续测试时间不得少于4 h),得到主轴温升曲线如图5,其中主轴前端盖温度T2、前轴承温度T3、主轴中间温度T4、后轴承温度T5及外环境温度T1。通过温升图可以看出,主轴前端盖和前轴承处的温升较迅速,100 min时已经到达39.5℃,而主轴中间和后轴承也有温升,但幅度不大。通过主轴热变形夹具测量到的主轴热变形漂移量如图6所示,其中S2、S5为X轴方向热漂移变形量,S1、S4为Y轴方向热漂移变形量,S3为Z轴方向热漂移变形量。从图中可知,X轴方向热漂移较大,100 min时达到10 μm,而Y轴方向相比较小才5 μm,变化最大的是 Z轴方向,100 min时达到43 μm。主轴热变形后在X、Y方向倾斜度(相对于初始位置)如图7所示。从图中可知,X轴方向倾斜误差较大,100 min时倾斜角已达到0.143 28°,这与在该方向的热变形漂移量是相对应的;而Y轴方向变化不大。
通过上述步骤,根据 ANSI/ASME B5.54-2005(USA)规定的国际测量标准,对另一主轴连续测量24 h的主轴温升及热漂移情形如图8所示,热变形后倾斜误差如图9所示。从图中可知,该主轴Z轴方向最大位移是32 μm,主轴热变形后倾斜误差是0.119 4°。
通过上述实时测量可以看出,由于主轴工作条件、工况和结构等不同因素,造成测出的热变形等结果也不尽相同:有的热变形明显,而有的由于冷却效果好而热变形较小。所以应针对不同主轴及其所处环境,采取不同的补偿数据。
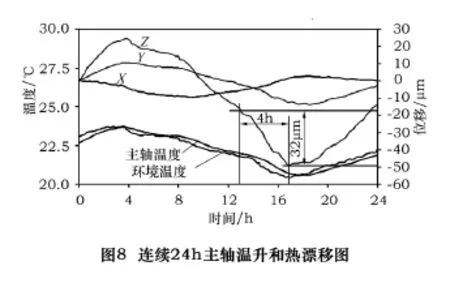
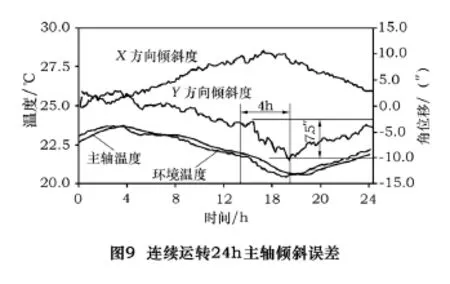
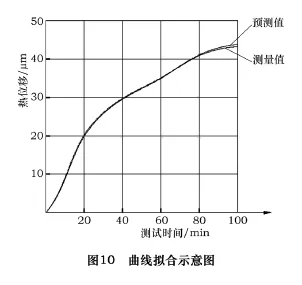
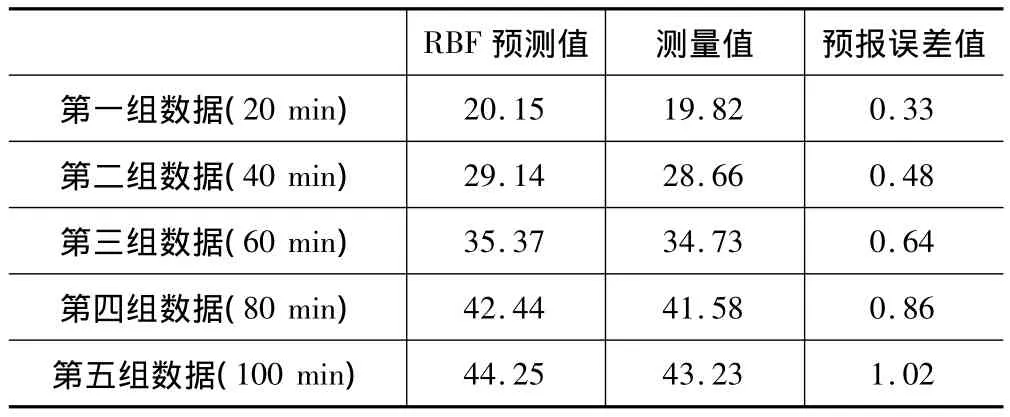
表1 预测值与测量值比较 μm
而基于RBF神经网络,以图3的主轴3个温度传感器点为温度敏感点,在主轴转速为1 000 r/min下的温度值和主轴前端的热变形量作为测试样本,建立主轴热误差数学模型。将测试样本输入在MATLAB下运行的网络模型,查看主轴在1 000 r/min的速度下,20 min、40 min、60 min、80 min、100 min 的预报结果,其预测值见表1,拟合曲线见图10。总的预报误差平方和SSE为2.53 μm,程序运行时间为0.02 s。图中,虚线代表RBF神经网络预测值,实线代表用API主轴测量系统所测的测量值。
3 结语
本文运用RBF神经网络对主轴热误差建立了数学模型,结合API主轴测量系统对电主轴进行了热变形漂移研究。由图10实验分析可以看出,利用RBF神经网络预测的主轴变形量与API主轴测量系统实验所得测量值相差在3%以内。温升对主轴的加工精度影响很大,主轴在X、Y、Z三个方向都有较大的变化,同时,该测量系统还首次测量出了主轴的倾斜误差,为下一步的实时误差补偿和机床加工精度的提高奠定了理论和实践基础。
[1]Postlethwaite S R,Allen J P,Ford D G.Machine tool thermal error reduction - an appraisal[J].Proceedings of the Institution of Mechanical Engineers,Part B:Journal of Engineering Manufacture.1999,213(B1):1-9.
[2]梁允奇.机械制造中的传热与热变形基础[M].北京:机械工业出版社,1982.
[3]Chang C,Ling C,Chao C,et al.A theory thermal growth control techniques of high speed spindles[C].Seoul,Korea,Republic of:Inst.of Elec.and Elec.Eng.Computer Society,2008.
[4]Bryan J B.International status if thermal error research[J].Annals CIRP,1969(16):203-215.
[5]Mcclure.E R.Significance of thermal effect in manufactuing and metrology[J].Annals CIRP,1967(15):61 -66.
[6]Donaldson R,Thompson D C.Design and performance of a small precision CNC turning machine[J].Annals CIRP,1986,35(1).
[7]张伯霖,肖曙红,郭军.高速电主轴热结构耦合特性的有限元分析[J].机械设计与制造,2008(09):96-98.
[8]Ching Feng C,Chao Shui L,Ching Yi C,et al.Theory thermal growth control techniques of high speed spindles[C].Piscataway,NJ,USA:IEEE,2008.
[9]郭策,孙庆鸿.高速高精度数控车床主轴系统的热特性分析及热变形计算[J].东南大学学报:自然科学版,2005,35(231-234).
[10]Li Y X,Yang J G,Li Y Y,et al.Study on the application of the combined prediction modeling method to thermal error modeling on NC machine tools[J].Key Engineering Materials,2007,329:779 -784.
[11]Bossmanns B,Tu J F.A thermal model for high speed motorized spindles[J].International Journal of Machine Tools &Manufacture,1999(39):1345-1366.
[12]杜正春,杨建国,窦小龙,等.基于RBF神经网络的数控车床热误差建模[J].上海交通大学学报,2003(1).

