饱和土结构性参数演化规律及其简化模型研究

胡 伟，韩建刚，李光范

（海南大学 土木建筑工程学院，海口 570228）

1 引 言

土的结构性是土颗粒空间排列和粒间联结作用的力学效应[1－2]。实践表明：绝大多数天然土体都具有一定的结构性，且这种结构性对土体的工程特性有着很大的影响[3]。土体结构性研究的关键是要找到一个合适的定量化指标，建立岩土微结构与宏观力学效应之间的定量表达关系，发现岩土结构性及其所反映出的宏观力学效应的变化。文献[4]建议了根据原状土、饱和原状土和重塑土的压缩试验，基于压缩应变来定义和测定土结构性定量参数，把这类结构性参数归为应变型。文献[5]中使用的是孔隙比，也应属于这一类型。文献[6]中建议对原状土、饱和原状土以及相同含水率和干密度的重塑土进行三轴试验，依据它们的应力-应变曲线，以得到的给定应变条件下不同结构状态土各自的主应力差定义的综合结构势来反映扰动、浸水和加荷作用下的结构性变化。把这类结构性参数归为应力型，文献[7]中对动荷载作用下土体结构性参数的定义也属于这一类型。文献[8－9]中把非均匀的结构性土体看成由胶结块和软弱带组成的二元介质材料。为了定量的评价受荷中两者各自所起的作用，引入了剪切抗力分担率系数，此系数是对不同的试样达到破坏状态时软弱带所发挥的剪切抗力的比率。显然这里定义的结构性参数对应于土体的破坏状态。为了得到结构性参数加载全过程的定量评价，本文以饱和黄土为研究对象，引入两类超固结比的概念，在对原状饱和黄土、重塑饱和黄土进行三轴不排水剪切试验的基础上，将应力分担率推广到任意变形下的情形，定义了结构性发挥系数，并给出了其计算模式及相应的理论计算公式。

2 结构性量化试验研究

表1 结构性饱和黄土指标Table 1 Property indexes of structural saturated loess

考虑到工程实际，定义两类超固结比：第1类是前期固结压力不同，当前固结围压相同而形成的第1类超固结状态β1，如图1中的A、B点所示。

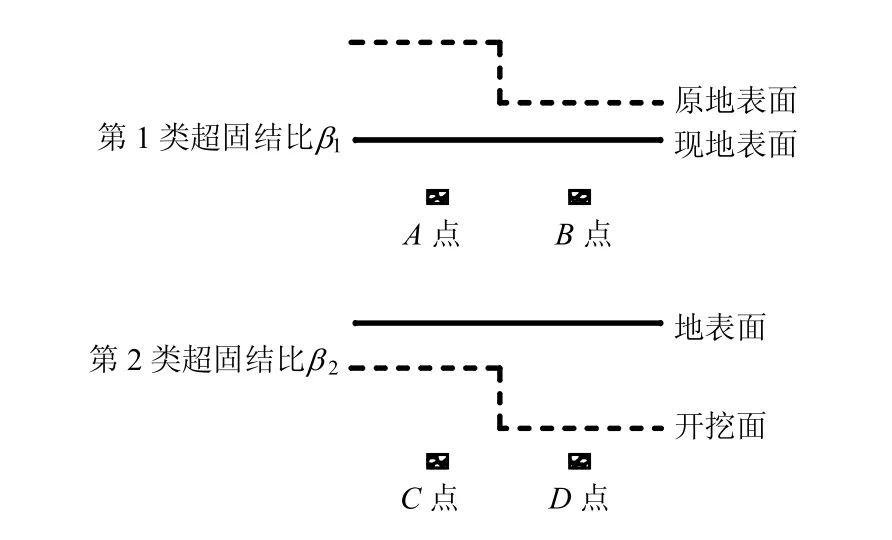
图1 两类超固结比定义示意图Fig.1 Sketch maps of two over-consolidation ratios

此类固结比适用于由于开挖而引起的超固结状态，当前应力状态清楚的；第2类是前期固结压力相同，当前固结围压不同而形成的第2类超固结状态β2，如图1中的C、D点所示。此类超固结比适用于液化引起的似超固结状态，前期固结压力是已知的。

试验中，第1类超固结比试样通过加载到不同围压，固结后卸载到相同的当前围压获得不同的超固结比β1，如4个试样分别在50、75、100、200 kPa围压下固结后均卸载至50 kPa，得到的第1类超固结比分别为：β1=1、β1=1.5、β1=2.0、β1=4.0；第二类超固结比试样通过加载到相同围压，固结后卸载到不同的当前围压获得不同的超固结比β2，如4个试样先均在 100 kPa围压下固结后分别卸载至100、66.7、50、25 kPa得到的第2类超固结比分别为：β2=1、β2=1.5、β2=2.0、β2=4.0。将对应的饱和原状黄土和完全重塑饱和黄土三轴剪切试验所得的应力水平-应变水平曲线绘制在同一 σi- ei坐标下，如图2所示，其中应力水平σi、应变水平ei分别定义如下：

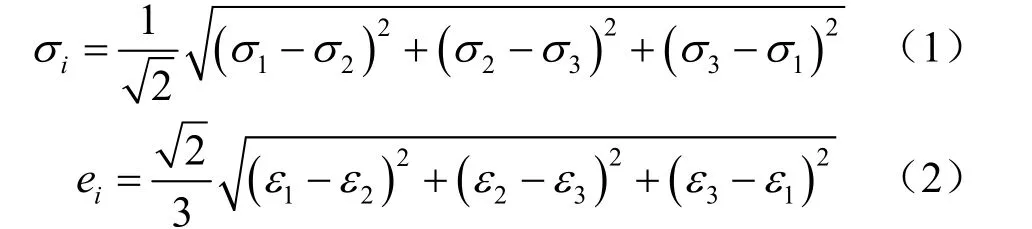
在图2所示的 σi-ei关系图中，对应相同的应变水平ei，饱和原状黄土对应的应力水平为σis，完全重塑饱和黄土为σir，则定义应力分担率系数如下：

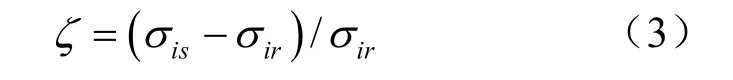
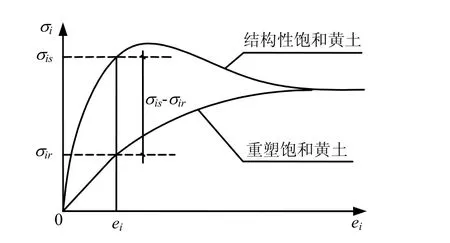
图2 应力分担率计算原理Fig.2 The calculation of stress share ratio

ζ表示相同围压下不同应变水平时土体结构性在抵抗剪切变形中的贡献比例，它是应变水平ei的函数，即 ζ= f(ei)。如果针对不同围压下进行类似的定义，则可以得到相同应变水平不同围压时ζ的变化规律。

图3中给出了3种围压下正常固结试样的典型ζ- ei曲线。试验中以应变水平10%为破坏标准，即此时土体的结构性被完全破坏，应力分担率为 0。从图中可以看出，应力分担率随应变水平的变化曲线明显分为两个阶段：第1阶段几乎表现为线性增长，也就是此阶段结构性是处于线性发挥状态；当应变达到一定值后，应力分担率出现峰值，随后结构性开始发生破坏，进入到第2阶段。在此阶段内，应力分担率随着变形的增长而减小，呈双曲线变化，变化速率先快后慢，最终趋于 0，土体退化为完全重塑状态。上述变化规律表明，在很小变形下，结构性强度就能被充分发挥出来，并达到峰值，随即又被迅速破坏。这也意味着结构性对变形初期土体力学性能的影响是相当显著的，随着变形的增大，其影响也越来越小。从图中还可以看出，固结围压越小，应力分担率的峰值越大。这表明固结压力对结构性有破坏作用，固结围压越小，结构性的影响则相对越大。

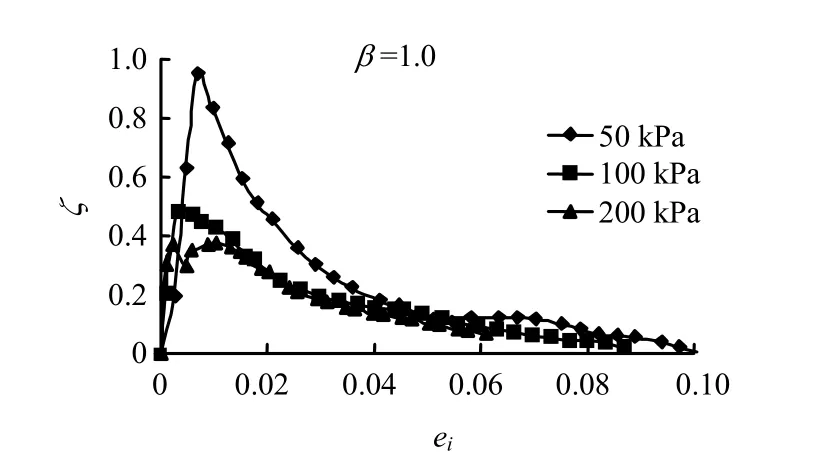
图3 正常固结土ζ -ei 关系曲线Fig.3 ζ -ei curves of normal consolidated soil

3 结构性演化计算模型

上述定义的应力分担率系数虽然很好地反映了结构性的演化规律，但在不同情况下这种规律并不具有归一性，不便于实际应用。对应力分担率2阶段变化特点的进一步分析可知，土体结构性的破坏具有相应的应变阈值，在变形未达到该阈值之前发生卸载的话，土体的结构性是能完全恢复的，在下一次再加载中结构性仍能发挥到其最大值；当变形超过阈值后，土体的结构性就已部分被破坏，在后期的加载中，已无法发挥出其最大值。据此定义结构性发挥系数η如下所示，其中ζmax为应力分担率峰值。

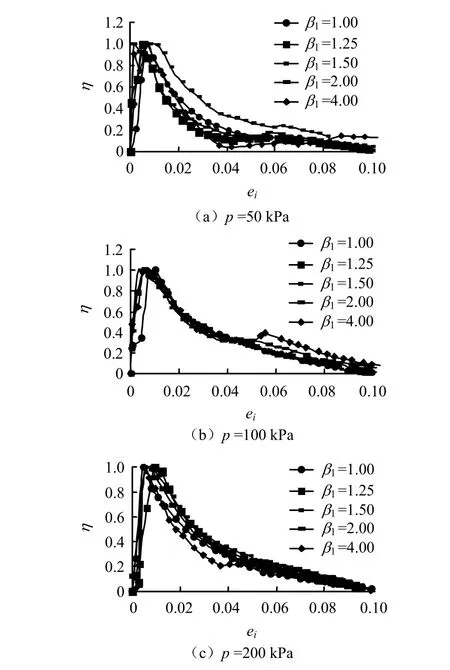
图4 不同第1类超固结比下η -ei变化规律Fig.4 η -ei curves under different first types of over-consolidated ratios

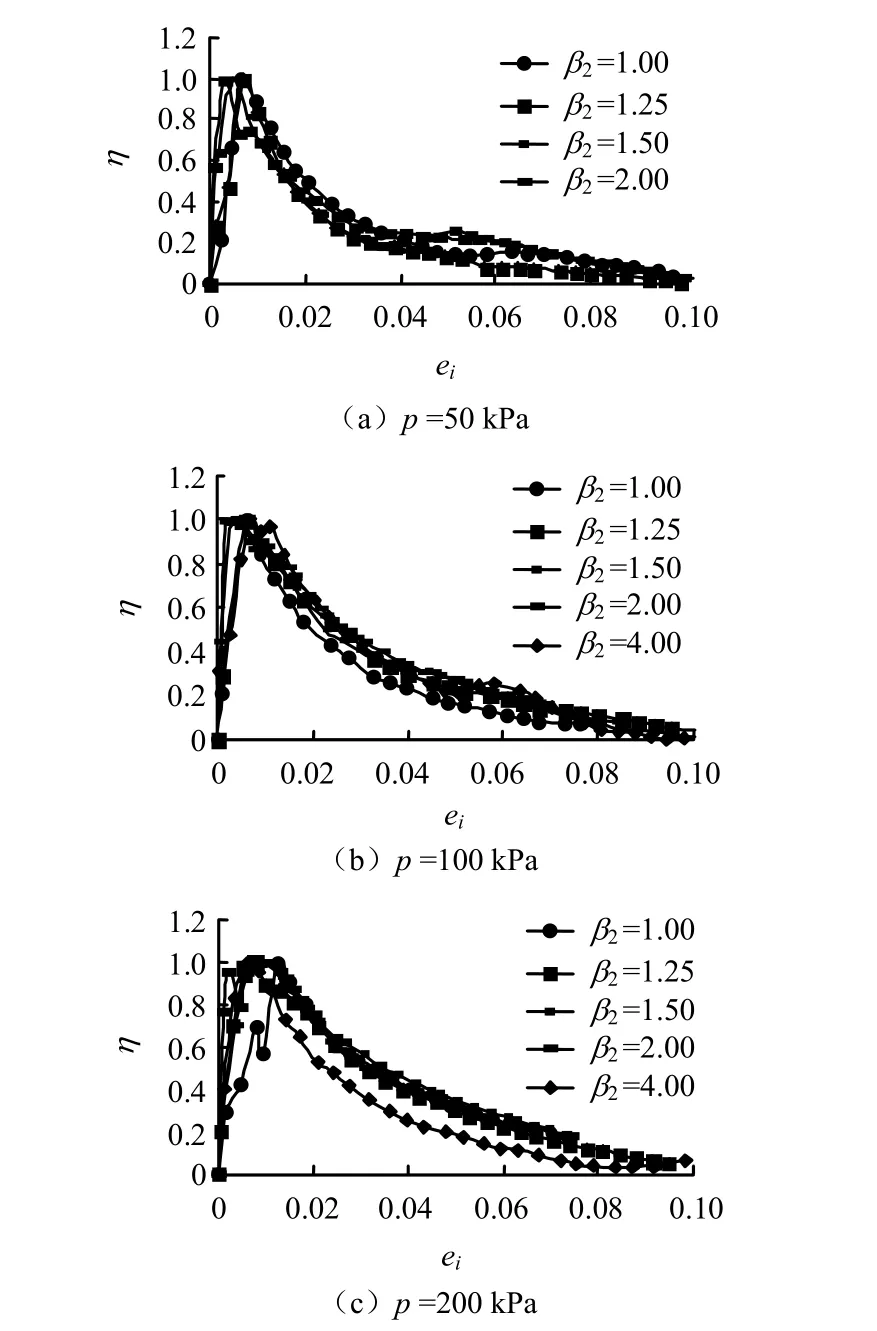
图5 不同第2类超固结比下η -ei变化规律Fig.5 η -ei curves under different second types of over-consolidated ratios

不同围压、两类超固结比下结构性发挥系数随变形水平的变化规律如图4、5所示。从图中可以看出：结构性发挥系数随应变水平的变化分为两段：峰值应变之前，η呈线性增长；峰值之后，则随着变形的增大呈对数规律减小。上述规律对于不同的围压下的不同超固结比，都具有很好的稳定性。图6为3种围压的两种不同类型超固结比试样的结构性发挥系数随变形水平的变化规律。从图中可以看出，两类超固结比下，结构性发挥系数的变化规律也具有较好的归一性，故可以用同一计算模式进行计算。这也意味着当第一类超固结土样当前围压和第2类超固结土样前期固结压力相同时，两者结构性演化规律的的模拟计算中所不同的是应力分担率的峰值ζmax不一样，结构性发挥系数计算模式是相同的。

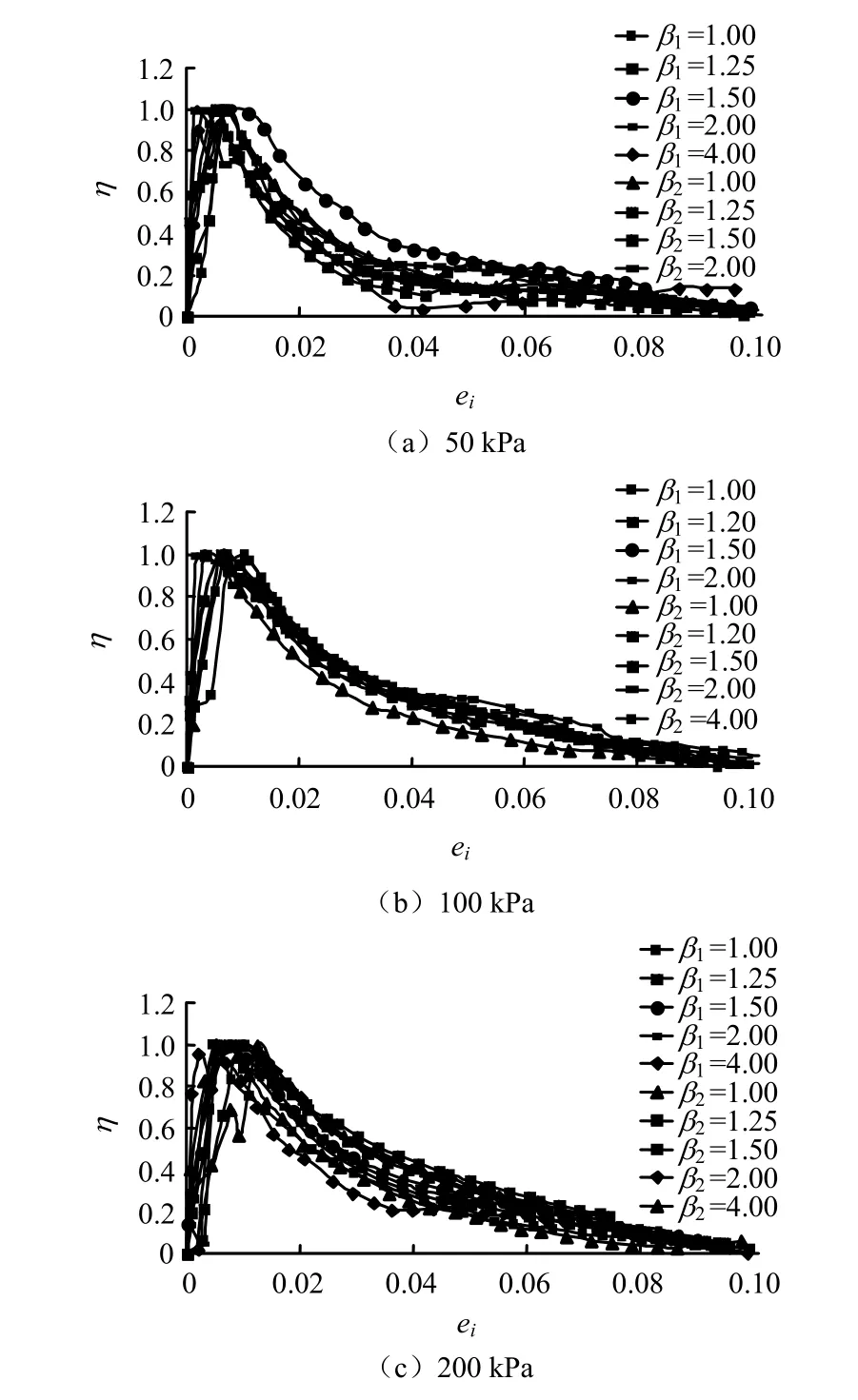
图6 相同围压、两类超固结比下η -ei变化规律Fig.6 η -ei curves under different two types of over-consolidated ratios

综合上述分析可知，结构性发挥系数的演化规律可采用如图7所示的计算模式。

相应的理论式如式（5）所示，其中独立的参数只有2个，即结构性初始破坏应变阈值ei,sta、结构完全破坏应变值ei,ult，其余3个参数a、b、c均为计算参数。

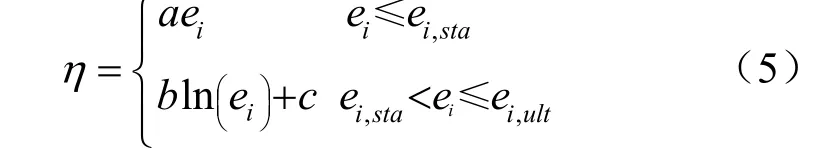
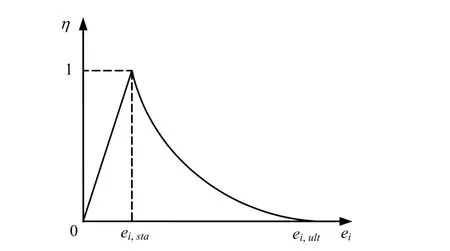
图7 η 计算模式Fig.7 The calculation model of η

25个试验结果的统计如图8所示，离散系数为0.067 7，由此可知，对于给定的土样，应变阈值ei,sta具有较好的稳定性。本次试验土样ei,sta平均值为0.655%，即当 ei＜ 0.655%时，η呈线性增长；此时ηmax= 1；结构性完全破坏时对应的应变水平取ei,ult= 10%，即当 ei≥ 10%时，η=0；当0.655%＜ei＜ 10%时，由一对数曲线来确定。根据边界条件可以确定出 a=152.7、b=-0.367、c=- 0.845。则任意应变水平下结构性应力分担率由一个3段式函数确定：

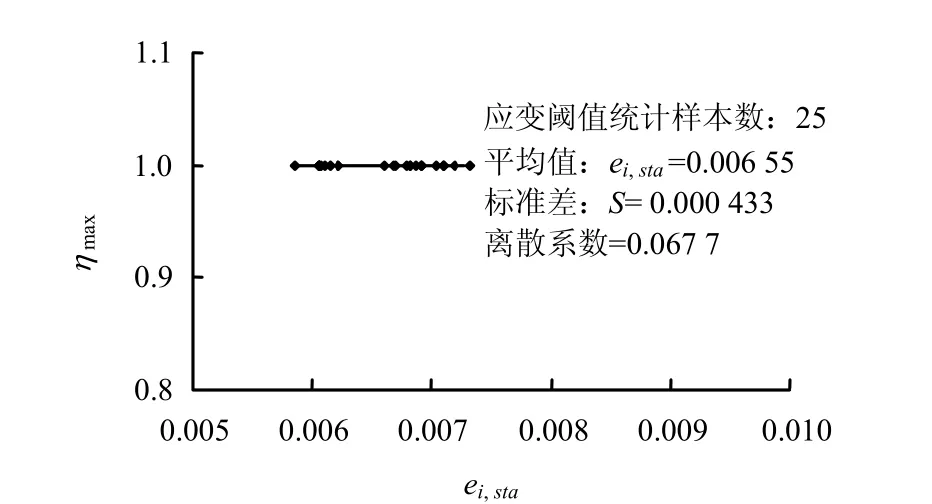
图8 应变阈值统计Fig.8 The statistics of strain threshold value

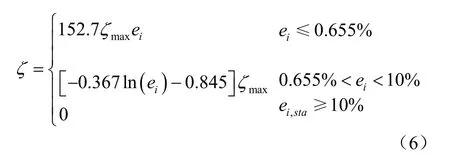
4 计算模型验证

由式（6）可知，如果土体破坏标准事先确定的话，确定应力分担率的演化规律也仅需2个参数，即结构性初始破坏应变阀值ei,sta和该应变水平对应的应力分担率峰值ζmax。应力分担率一旦确定，若重塑土的应力-应变关系表示为 σi= f(ei)，则结构性土体的应力-应变关系可表示为

图9为不同围压下(50，100，200 kPa)重塑土、结构性土的应力-应变试验曲线和公式计算曲线的对比图。从图中可以看出，计算和试验曲线符合得较好，这证明了本文提出的结构性量化计算模式的有效性。

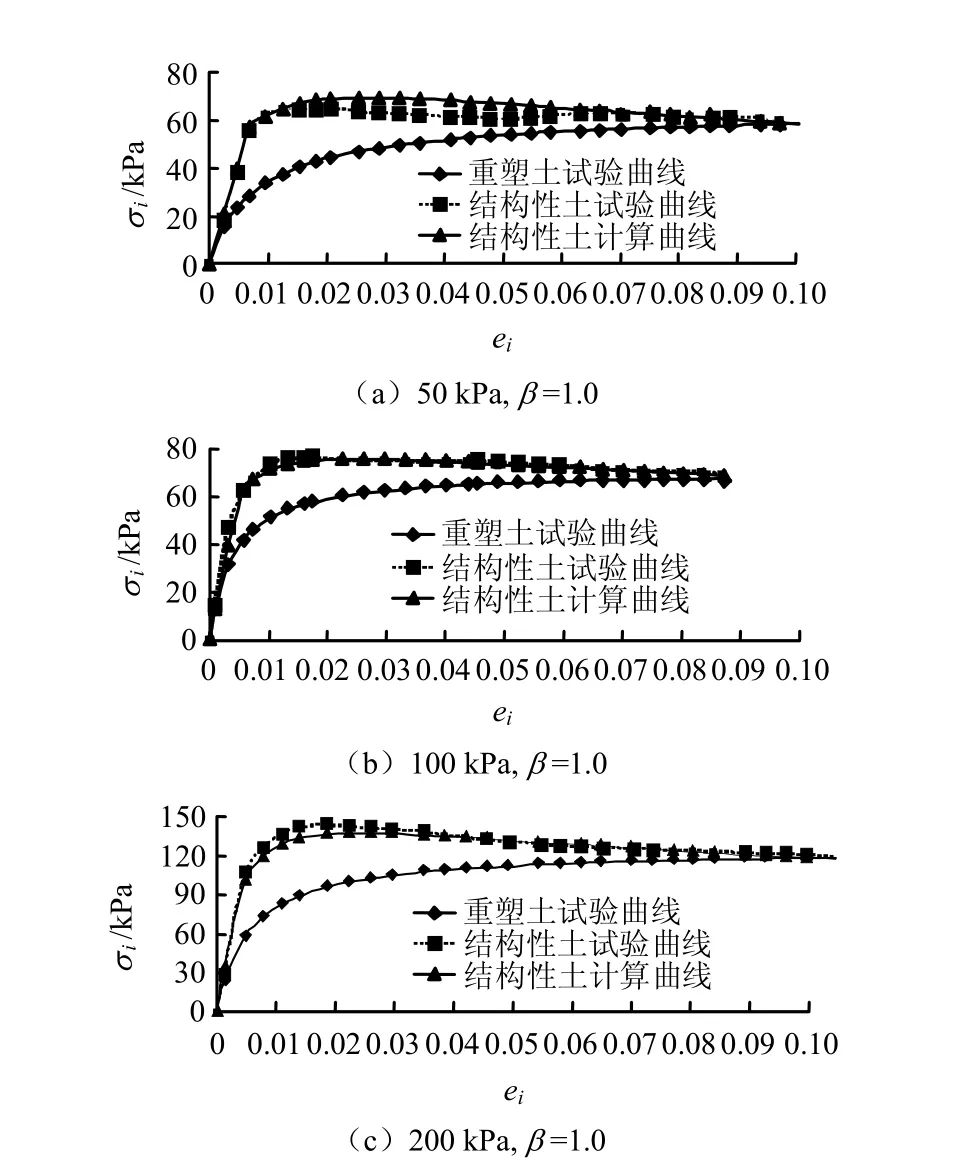
图9 应力-应变试验、计算曲线对比Fig.9 Comparison between test’s stress-strain relationships and calculation ones

5 结 语

结合工程实际，本文引入了两类超固结比的概念，对不同围压下的两类不同超固结比饱和原状、重塑黄土试样进行三轴固结不排水剪切试验。结合应力分担率的定义对试验所得的应力-应变曲线进行整理，获得了应力分担率随应变水平呈两阶段特征的变化曲线。进一步引入结构性发挥系数的概念对应力分担率曲线进行归一化处理，并由此提出了结构性的计算模式和相应的理论计算公式。理论公式为一个3段式函数，形式简单、参数少且具有较好的稳定性。对比分析表明：公式计算和试验结果具有很好的一致性，证明了本文提出的结构性量化计算模式的有效性。

[1]邵生俊, 周飞飞, 龙吉勇. 原状黄土结构性及其定量化参数研究[J]. 岩土工程学报, 2004, 26(4): 531－536.SHAO Sheng-jun, ZHOU Fei-fei, LONG Ji-yong.Structural properties of loess and its quantitative parameters[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(4): 531－536.

[2]宁树军, 张树光. 土的结构性对路基稳定的影响[J]. 沈阳大学学报, 2002, 14(4): 46－48.NING Shu-jun, ZHANG Shu-guang. Effect of soil’s configuration to roadbed stabilization[J]. Journal of Shenyang University, 2002, 14(4): 46－48.

[3]刘用海, 朱向荣, 吴健, 等. 宁波软土结构性成因及其对工程特性影响的研究[J]. 工业建筑, 2008, 38(3): 68－71.LIU Yong-hai, ZHU Xiang-rong, WU Jian, et al. Genetic analysis of soft soil structure and experiment on its influence engineering properties in Ningbo area[J].Industrial Construction, 2008, 38(3): 68－71.

[4]谢定义, 齐吉琳, 朱元林. 土的结构性参数及其与变形-强度的关系[J]. 水利学报, 1999, 10: 1－6.XIE Ding-yi, QI Ji-lin, ZHU Yuan-lin. Soil structure parameter and its relations to deformation and strength[J].Journal of Hydraulic Engineering, 1999, 10: 1－6.

[5]陈存礼, 胡再强, 高鹏. 原状黄土的结构性及其与变形特性关系研究[J]. 岩土力学, 2006, 27(11): 1891－1896.CHEN Cun-li, HU Zai-qiang, GAO Peng. Research on relationship between structure and deformation property of intact loess[J]. Rock and Soil Mechanics, 2006,27(11): 1891－1896.

[6]骆亚生, 谢定义. 复杂应力条件下土的结构性本构关系[J]. 四川大学学报(工程科学版), 2005, 37(5): 14－18.LUO Ya-sheng, XIE Ding-yi. Structural constitutive relation of soils under complex stress conditions[J].Journal of Sichuan University (Engineering Science Edition), 2005, 37(5): 14－18.

[7]陈存礼, 高鹏, 何军芳. 考虑结构性影响的原状黄土等效线性模型[J]. 岩土工程学报, 2007, 29 (9): 1130－1136.CHEN Cun-li, GAO Peng, HE Jun-fang. Equivalent linear model of intact loess considering structural effect[J].Chinese Journal of Geotechnical Engineering, 2007, 29(9): 1130－1136.

[8]刘恩龙, 沈珠江. 结构性土的强度准则[J]. 岩土工程学报, 2006, 28(10): 1248－1252.LIU En-long, SHEN Zhu-jiang. Strength criterion for structured soils[J]. Chinese Journal of Geotechnical Engineering , 2006, 28(10): 1248－1252.

[9]刘恩龙, 沈珠江. 结构性土的二元介质模型[J]. 水利学报, 2005, 36(4): 391－395.LIU En-long, SHEN Zhu-jiang. Binary medium model for structured soils[J]. Journal of Hydraulic Engineering,2005, 36(4): 391－395.

[10]杨振茂, 赵成刚, 王兰民. 饱和黄土的液化的试验研究[J]. 岩石力学与工程学报, 2005, 24(5): 864－871.YANG Zhen-mao, ZHAO Cheng-gang, WANG Lan-min.Testing study on saturated loess liquefaction[J]. Chinese Journal of Rock Mechanics and Engineering, 2005,24(5): 864－871.