三江平原地下水埋深灰色自记忆预测模型

吕 萍，刘 东，2，赵菲菲

（1．东北农业大学 水利与建筑学院，哈尔滨150030；2．东北农业大学 农林经济管理博士后科研流动站，哈尔滨150030）

三江平原是我国重要的商品粮基地，对我国粮食生产起着重要的保障作用。1986－2005年，三江平原水稻种植面积从57．7万h m2增加到150．9万h m2［1］。由于水田面积的迅速扩大，地下水开采量也迅速增加，加之人为浪费严重及管理不善，使得三江平原多年平均地下水埋深持续增加，“吊泵”和局部超采现象时有发生［2］，地下水资源平衡遭到了严重的破坏。

地下水埋深由于受诸多自然和人为因素的影响而呈现复杂的非线性变化过程［3］，预测和分析研究地下水动态变化过程，有助于正确估算及合理开发利用地下水资源。地下水埋深动态预测传统的方法有确定性模型和随机性模型，其中确定性模型的求解主要有解析法、数值法和物理模拟法；随机性模型有回归分析法、频谱分析法等，但由于这些模型本身复杂或大量的物理参数难以获得，因而不便在实际中应用［4－5］。

本研究采用灰色微分方程与自记忆原理相结合的方法建立自记忆方程预报模型，并应用于三江平原七星农场地下水埋深序列的模拟及预测。该方程避免了多种影响因素数据的收集整理，只涉及地下水埋深观测序列本身，方便实用且具有较好的预测精度。

1 建模思路

诸多自然现象和社会经济现象都是有规律的辨证发展过程，其运动变化都有一定的惯性，这种惯性就表现为系统的记忆性［6］。自记忆性强调系统的变化总是与其历史行为相联系，或者说系统总会记得它的过去，因此可以通过引入记忆函数建立系统的自记忆方程，从而预测系统未来的变化［7］。对于有微分方程描述的动力系统，可以建立相应的自记忆模型，通过实际应用［7－10］，证明它能显著提高预报准确率。对于地下水系统一般只有一系列动态观测值，这时可把现有的许多观测资料看作是描述实际非线性动力系统动力模式的一系列特解，通过一定的方法反演出描写系统的非线性动力模式后，便可建立自记忆模型进行模拟或预报［7］。

2 灰色自记忆模型

2．1 灰色GM（1，1）微分方程

地下水埋深时间序列受众多因素影响，具有很大的不确定性，因此可用灰色系统方法进行分析研究［9］。GM（1，1）是用一阶线性常微分方程来描述灰色系统单序列动态情况的模型，可以对水文单因素进行中长期预报［6，10－11］。

设地下水埋深观测序列为x（t），t＝1，2，…，n。为消除数据量级上的差别影响，首先对序列进行归一化预处理［12］，本文采用除以序列最大值方法得到处理数据序列：

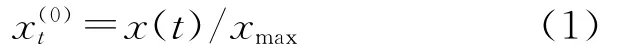
式中：xmax——序列原始数据的最大值。对序列作一次累加生成：

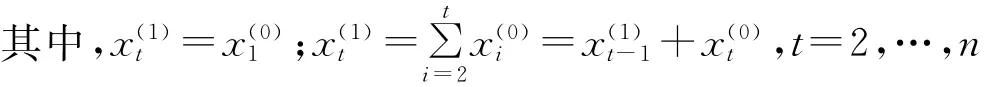
（3）

得到的新数据序列与原始数据序列相比较，其随机程度大大弱化，平稳程度大大增加。其变化趋势可用一阶微分方程描述为

式中，参数a和u可通过最小二乘法得到，即

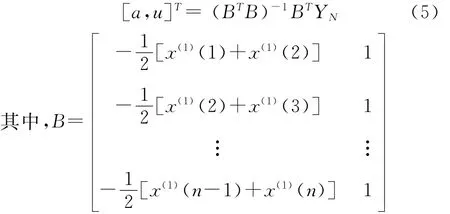
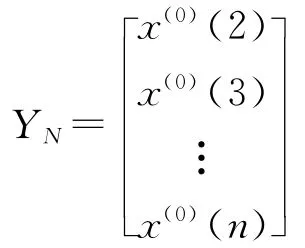
在式 （4）中，令 d x（1）／d t＝F（x，t），移项后得GM（1，1）微分方程式为

F（x，t）＝u－ax（1）（6）

2．2 自记忆模型

将导出的灰色微分方程作为动力核，运用自记忆性原理建立月地下水埋深时间序列的自记忆模型［6，9，12－13］。

对时间序列的多个时次ti（i＝－p，－p＋1，…，0，1），t0为初始时次，t1为预测时次，p为回溯阶，引进记忆函数β（t），对F（x，t）求t－p至t1的加权积分，运用分部积分和微积分中值定理得出一个差分－积分方程：

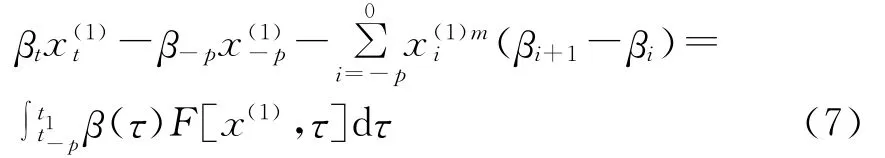
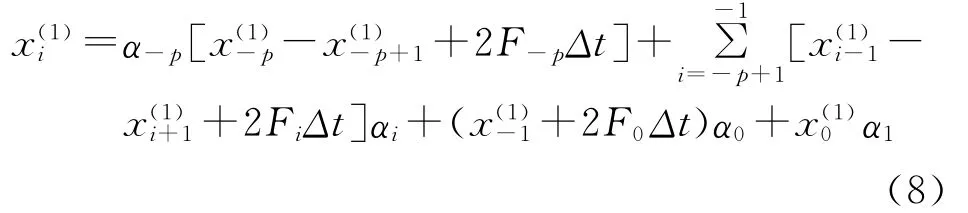
式中：Δt——序列时间间隔，一般取为1；Fi——式（6）中的F（x，t）。

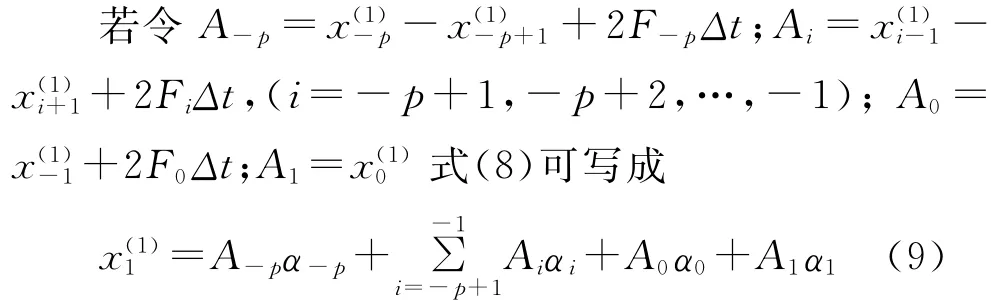
式（9）即灰色自记忆模型预测方程。模型记忆系数αi可用最小二乘法估算，顺次取累加生成序列式（2）中p＋2个数据为一组，则有L＝n－（p＋1）组数据，将每组数据代入式（9），则可得到一个L行p＋2列矩阵：

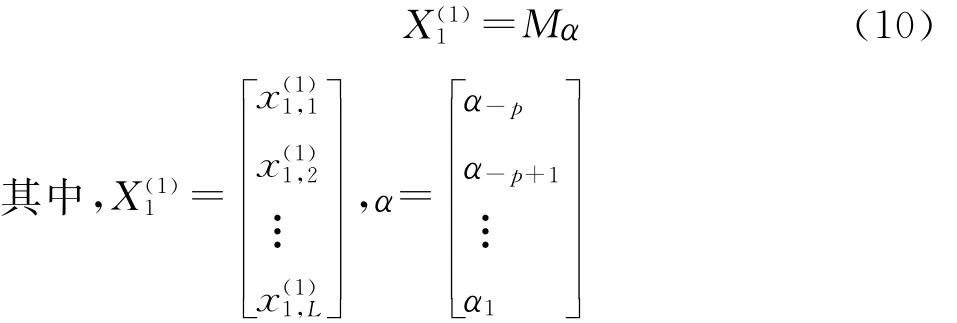
式（10）中，α的最小二乘解为：α＝（MTM）－1MTX（1）1。

3 应用实例

3．1 数据资料

根据三江平原七星农场1997－2007年132个月的月地下水埋深观测资料，从中选取前120个月（1997－2006年）的资料进行建模，用2007年12个月的资料对模型进行试报检验，并预测2008年12个月的地下水埋深。

3．2 灰色自记忆模型建立

首先求得归一化处理后地下水埋深时间序列的微分方程为：

F（x，t）＝0．4731＋0．005407x（1）

然后按照式（9）建立灰色自记忆预测方程，取回溯阶数p为11，则有：

经计算，模型记忆系数：α－11＝－16．648，α－10＝16．71，α－9＝－16．956，α－8＝17．378，α－7＝－17．392，α－6＝17．447，α－5＝－17．254，α－4＝17．378，α－3＝－17．478，α－2＝17．783，α－1＝ －17．475，α0＝16．626，α1＝－15．626。

将计算结果乘以最大值并进行累减还原，用所建模型模拟1998年2月至2006年12月的107个月地下水埋深值（对应编号为14－120），因回溯阶及累减原因，1997年1月至1998年1月无拟合值（对应编号为1－13）；对2007年12个月的地下水埋深值（对应编号为121－132）进行试报，模型拟合值、预测值和实测值见图1，预测结果与实测值的比较见表1。

图1 七星农场月地下水埋深实测值与拟合值、预测值的比较

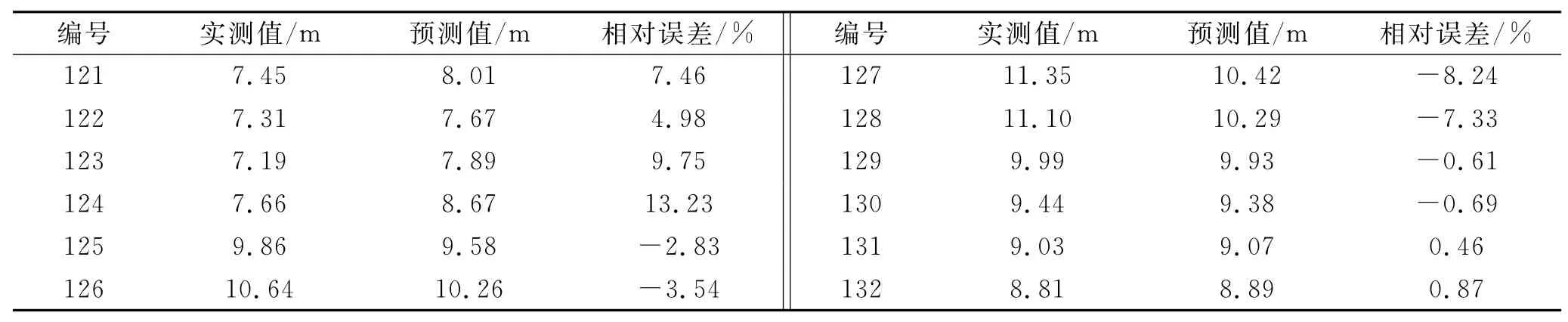
表1 七星农场月地下水埋深实测值与灰色自记忆模型预测值的比较（2007年1－12月）

应用上述数据资料及模型对2008年12个月地下水埋深预测结果见图2。

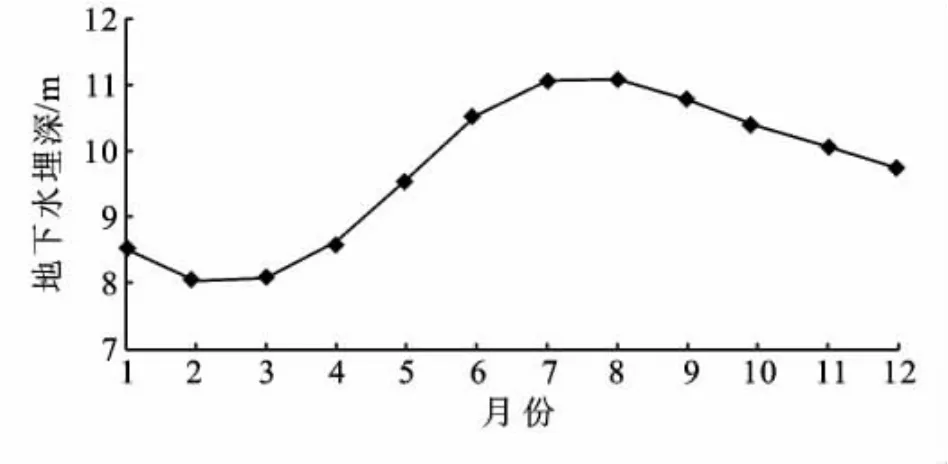
图2 2008年七星农场月地下水埋深预测结果

3．3 模型结果分析

由图1可看出，模型拟合效果较好，能很好地拟合变化趋势和序列中的极值，体现出时间序列的波动特征。计算结果表明，在拟合的107个月中，相对误差在20%以上的有7个，占拟合月份的6．54%；相对误差在10%以下的有85个月，占拟合月份的79．44%；平均相对误差为7．31%。预测结果（表1）表明，在试报的12个月中，只有一个月相对误差在10%以上，占预测月份的8．33%，58．33%的月份相对误差在4%以内，平均相对误差为5%。

编号65，66，113和114的4个月份分别对应为2002年5月、6月和2006年5月、6月，这几个月份的拟合值与实测值有较大偏差。经分析认为，以上4个月份受当时气候影响，干旱严重，用于灌溉的地下水量激增，导致地下水埋深在短时期内急剧增加，地下水位在这几个月份有较大波动，所以在预测时出现了滞后和偏离的情况。

2008年地下水埋深的预测值较好地体现了地下水埋深的季节性波动特征，反映了地下水埋深逐年加深的变化趋势。

4 结 论

（1）灰色自记忆模型是一种确定性与不确定性相结合的方法，具有简洁实用的优点。模型计算只涉及地下水埋深观测序列本身，无需其它影响因素的观测资料，将由灰色理论导出的GM（1，1）微分方程作为动力核较其他方法简单方便，模型结构简单，易于编程计算。

（2）通过实例验证，灰色自记忆模型充分利用了多个历史观测值信息，能够显著提高预报的准确率，具有较好的模拟和预测效果。其预测结果比较科学合理，可为三江平原水资源合理开发利用提供参考依据。

（3）研究结果表明，三江平原七星农场的地下水埋深逐年加深趋势显著，不利于区域的可持续发展，建议当地严格控制地下水开采量，兴建地表水控制工程，开源节流，防止地下水资源进一步恶化，同时应大力推广节水灌溉技术，以提高有限水资源的利用效率。

［1］ 黄妮，刘殿伟，王宗明．1986－2005年三江平原水田与旱地的转化特征［J］．资源科学，2009，31（2）：324－329．

［2］ 刘东，付强，孟军．集对分析法在三江平原井灌区地下水资源承载力评价中的应用［J］．中国农村水利水电，2009（2）：1－4．

［3］ 李荣峰，沈冰，张金凯．考虑周期性变化的地下水埋深预测自记忆模型［J］．农业工程学报，2005，21（7）：34－37．

［4］ 张蔚榛，沈荣开．地下水文与地下水调控［M］．北京：中国水利电力出版社，1998．

［5］ 周维博．人工神经网络理论在井渠结合灌区地下水动态预测中的应用［J］．西北水资源与水工程，2003，14（2）：5－9．

［6］ 曹鸿兴．动力系统自忆性原理：预报和计算应用［M］．北京：地质出版社，2002．

［7］ 李荣峰．地下水动态预测的自记忆性模型及其应用研究［J］．山西水利科技，2005（1）：6－8．

［8］ 沈冰，李荣峰，黄领梅，等．年径流预测的灰色自记忆模型［J］．西北农林科技大学学报：自然科学版，2005，33（4）：132－134，138．

［9］ 解苗苗，王文圣，王红芳．灰色自记忆模型在年径流预测中的应用［J］．水电能源科学，2007，25（2）：8－9，4．

［10］ 沈冰，刘敏，黄领梅．灰色自记忆模型及其在新疆和田地下水埋深预测中的应用［J］．西北农林科技大学学报：自然科学版，2006，34（11）：223－226．

［11］ 徐建华．现代地理学中的数学方法［M］．北京：高等教育出版社，2004．

［12］ 李荣峰，沈冰，张金凯．作物生育期降雨量预测的灰色自记忆模型［J］．武汉大学学报，2005，38（3）：19－21，53．

［13］ 曹永忠，封国林，曹鸿兴，等．区域气候预报自记忆模式的研究与计算［J］．南京气象学院学报，1999，22（3）：387－391．

［14］ 陆君安，夏军，陈士华，等．动力系统的自记忆数值预报［J］．数学杂志，1998，18（增刊）：11－14．

［15］ 李荣峰．水文非线性时间序列分析的自记忆模型研究［D］．西安：西安理工大学，2005．