带挠性附件的航天器结构-姿态耦合动力学

王 钦,何星星,文援兰

(1.国防科学技术大学 航天与材料工程学院,湖南 长沙 410073;2.上海卫星工程研究所,上海 200240)

0 引言

当前,航天领域中大型挠性航天器所受的关注越来越广泛,挠性附件的复杂度也越来越高,在精确控制星体姿态的同时有效抑制柔性附件的振动,成为目前研究的重要方向[1]。挠性附件的运动需用无限自由度的分布参数描述,而挠性运动和刚体的姿态运动相互耦合,用常微分方程和偏微分方程共同描述的是非线性、非定常系统。特别是当附件结构非常复杂时,求解更难。柔性航天器动力学建模中,合理选择航天器数学建模方法和原理可简化推导过程并有助于提高模型的工程实用性,常用方法有离散坐标法、分布参数法、混合坐标法和正则模态法等[2]。工程中常用的参数法或有限元法,都是将无限自由度的系统转为有限自由度系统,再行求解[3]。

相关领域的研究取得了大量成果[4、5]。特别是随着计算机性能的提升,采用混合坐标系方法建立由刚体姿态坐标描述中心刚体的运动以及由离散模态坐标描述挠性附件的运动,截去高阶模态对姿态控制系统的影响,即可转化为有限自由度对系统的描述,这既能准确描述系统运动及动力学特性,又便于设计与分析控制系统。本文基于结构动力学及刚体运动学和动力学,建立多平台联合仿真系统,对航天器结构-姿态全系统进行性能了分析及评估。

1 理论建模

1.1 挠性附件振动特性

对航天器挠性附件结构动力学系统,由有限元方法的基本格式,可得系统的求解方程为

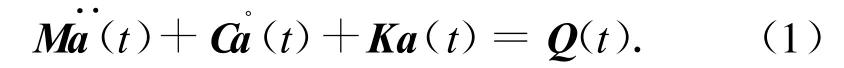
对式(1)的大型特征值问题,用有限元法求解时,常见的解法有矩阵反迭代法、子空间迭代法、里兹向量直接叠加法和Lanczos向量的直接叠加法等,可解得方程的特征值ωi及特征向量φi。在此基础上,将主坐标转化为模态坐标,即引入a(t)=Φx(t)=。此处：Φ为标准模态;n为模态阶次;x(t)为模态坐标,且x(t)=[x1… xn]T。由此可得模态坐标的动力学方程为

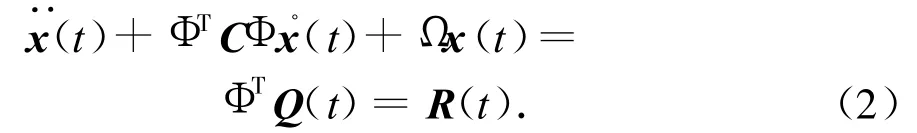
式中：Ω=diag[(ω1)2(ω2)2… (ωn)2];R(t)为模态坐标下的广义力。对应的初始条件转为：x0=ΦTMa0,。此处：a0为a的初值。

一般工程结构可视为结构型阻尼,根据Φ的正交性,有

式中;ξi为结构阻尼比。因此,此时原动力学方程可变为互相不耦合的二阶常微分方程

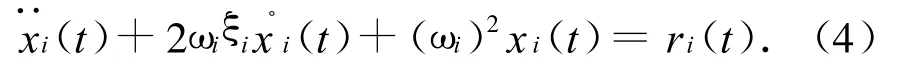
式中：i=1,2,…,n。求解式(4)即可获得每个振型的响应,将其叠加后,则每个节点的位移响应为

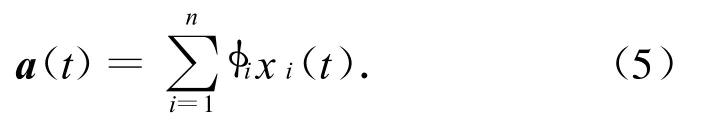
1.2 挠性附件-航天器姿态耦合动力学

对复杂的挠性附件结构,本文建立集中参数模型,用有限元法对系统进行离散化,建立有限自由度的动力学模型。

1.2.1 卫星运动线动量方程

设卫星由1个本体结构B和N个挠性附件组成,其中第i个挠性附件为Bi,如图1所示。建立惯性坐标系O1-x1y1z1。令卫星未变形时的整星质心位于点O,在点O处建立本体坐标系O-xyz;第i个挠性附件与卫星本体的连接点位于点Oi,在点Oi处建立挠性附件坐标系Oi-xiyizi,点Oi在O-xyz系的矢量为lpi。对第i个附件的任一质量元(点K)mik,在Oi-xiyizi系中的矢量位置为rik,卫星变形后的位移为uik。则第i个附件的任一质量元mik在O1-x1y1z1系中的线速度可表示为

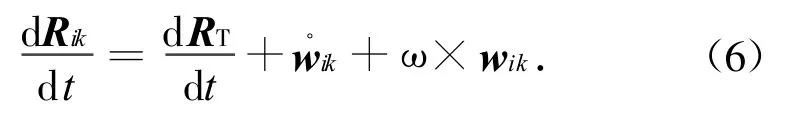
式中：wik为O-xyz系中卫星变形后点K的矢量坐标;ω为卫星的绝对速度。

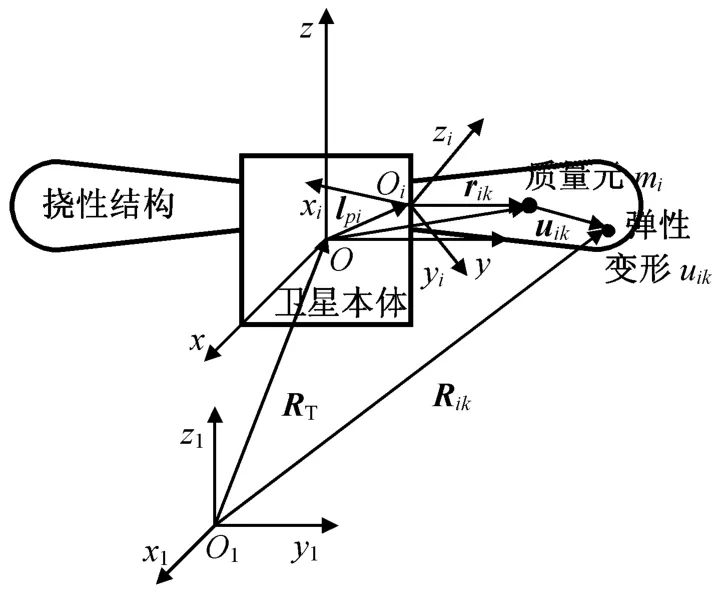
图1 卫星挠性附件结构Fig.1 Flexible appendages structure of satellite

设挠性变形为小量,变形后的位移函数亦为一阶小量,并作部分线性化处理,有wik=lpi+rik+uik,。

令VT=,则整星系统的线动量

式中：mT为整星系统质量。因点O为未变形前整星的质心,则=0,故P=mTVT+。

根据Newton第二定律,卫星运动的线动量方程为

式中：F为作用于卫星的外力。

在挠性附件的有限元计算中,令求解得到的挠性附件坐标系的结构振型为Φik=[φi1(rik) φi2(rik) … φin(rik)],k=1,2,…,n;固有频率为ωi1,ωi2,…,ωin。根据式(5),uik=Φikqi(t)。此处：qi(t)为附件结构离散的模态坐标,且qi(t)=[qi1(t) qi2(t) … qin(t)]。

设Oi-xiyizi系至O-xyz系的转换阵为TSiB,则线动量方程可改为

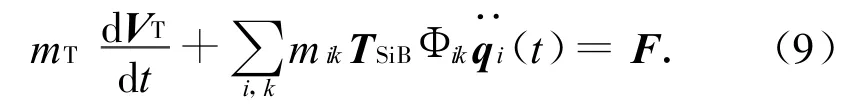
令BTrani为第i个挠性附件在O-xyz系中的平动耦合系数,且(此处BTrani为3×N维矩阵)。则

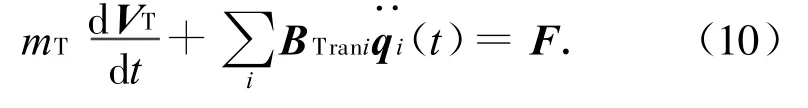
1.2.2 卫星角动量方程

设系统相对点O的绝对角动量为L,系统相对点O的力矩为MSat,则根据角动量定律,有

式中：IT为卫星未变形时的惯量阵。

将有限元法所得的振型函数代入式(11),并统一转为O-xyz系,即

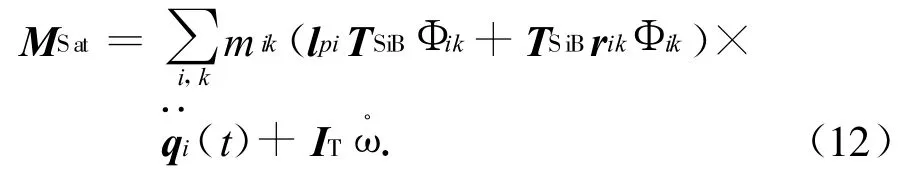
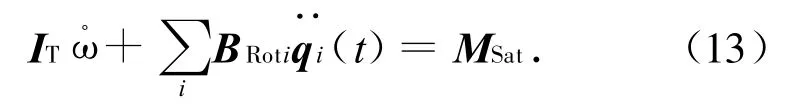
1.2.3 挠性附件运动方程

式中：Ψ(VT,ω)为仅含VT,ω的项。

仍用FEA结果uik=Φikq(t),并转为O-xyz系,再由振型函数的归一化性质,即(Φik)T(TSiB)TTSiBΦik=IN(此处：IN为单元阵),以及B Rot i,(B Rot i)T,附件动能可简化为

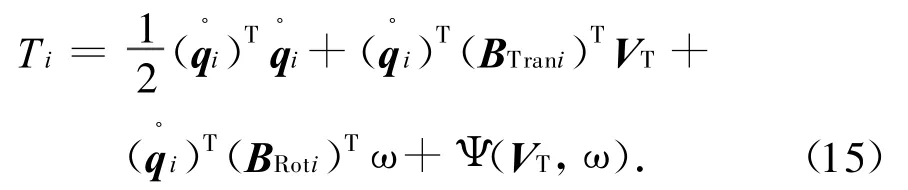
第i个挠性附件的应变能为

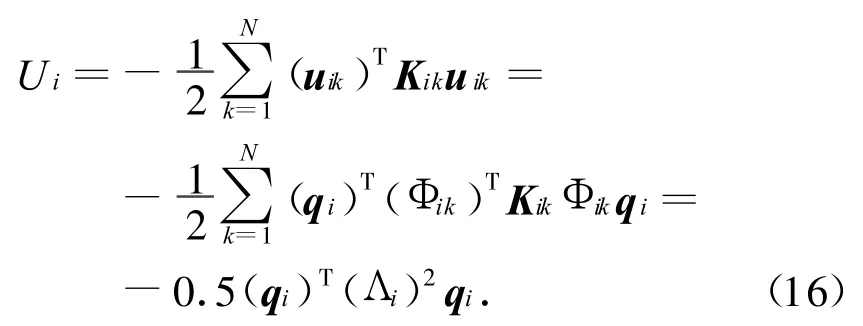
式中：Kik为第k个节点的刚度阵;(Λi)2=diag[(ωi1)2(ωi2)2… (ωiN)2]。

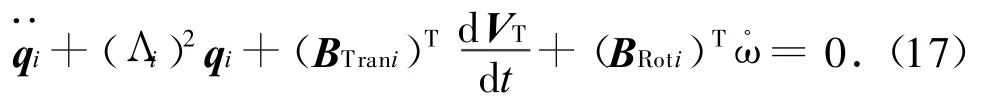
式中：i=1,2,…,k。

1.3 解耦分析

联立式(10)、(13)、(17),可得经线性化处理的卫星动力学方程组。若推广为更一般情况,即

a)考虑挠性附件的结构阻尼ζ=[ζ1ζ2…ζn]T时,式(17)应为

b)卫星带角动量为h的偏置动量轮时,式(13)应为

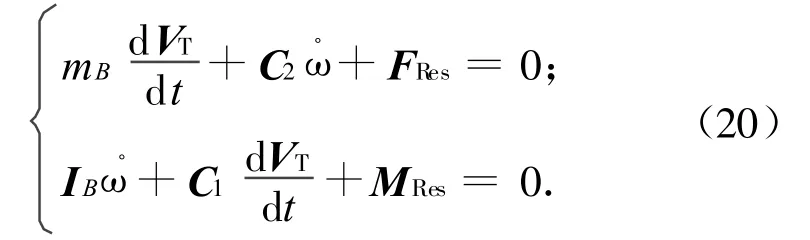
式中：

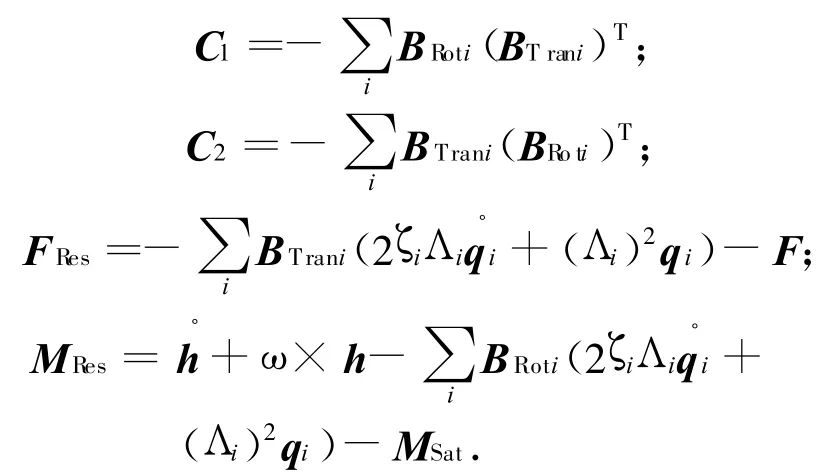
其中：IB-C1(mB)-1C2为等效惯量阵。式(21)表明：角加速度项已与线加速度项解耦。

2 联合仿真方法

卫星在轨运行过程中,大型挠性附件振动会使姿态动力学与结构动力学形成较紧密的耦合。大型挠性结构如太阳翼、天线、机械臂等会因卫星调姿引起激烈振动,姿控系统的活动部件如飞轮等在起动、停止和反向等过程中会对结构产生扰动,而这些振动又会影响卫星姿态。传统卫星设计方法中往往忽略姿态动力学与结构动力学的耦合效应,单独针对卫星姿态动力学与结构动力学进行分析和设计,故由此获得的方案在实际应用时的结果常与设计预期不符。

本文基于结构动力学平台和姿态动力学开发平台,实现对全系统进行联合仿真研究,其总体方案如图2所示。挠性附件的振动与卫星姿态系统的耦合主要通过挠性附件振动特性、卫星本体的姿态调整时产生的加速度和推力力矩形成耦合效应。此外,姿态调整时坐标系的变化会改变附件振型和耦合系数,增大了求解难度。为此,本文用数值模拟方法实现姿态控制系统与挠性附件结构动力学的同步仿真,姿态控制系统将姿态角、加速度和推力力矩等数据送至附件振动特性的计算;结构动力学分析将算得的附件结构固有频率、振型等数据送至姿态控制仿真系统,循环直至整个姿态系统稳定。

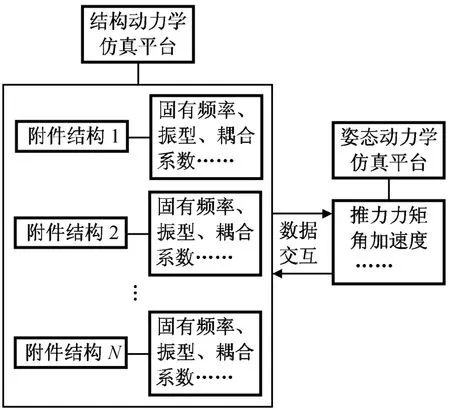
图2 联合仿真方案Fig.2 Co-simulation program

通过结构动力学平台ANSYS提供的APDL标量参数和数组参数可方便地实现有限元分析全过程的参数化,形成参数化的批处理文件,完成各种参数化分析,并可极大地提高分析效率。基于多刚体系统的卫星姿态动力学建模技术已相对成熟。在考虑挠性附件时,常采用混合坐标法建立挠性附件的振动方程和中心刚体的动力学方程,联合仿真程序流程如图3所示。

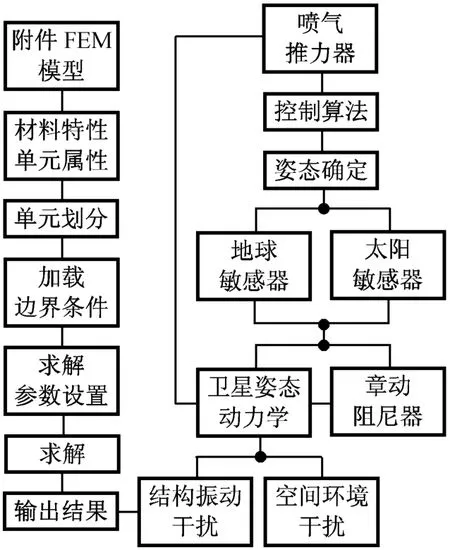
图3 联合仿真程序流程Fig.3 Program process of co-simulation

3 仿真结果与分析

3.1 挠性附件振动特性

以某双自旋卫星为例,以其中一星载天线作为卫星附件结构,如图4所示。该天线结构主要包括与卫星本体焊接的支撑板、半球柱网面结构体、信号发射外伸端及螺钉等附属构件。有限元建模时,忽略螺帽、螺钉等小型构件,对模型作部分简化。因支撑板与卫星本体相连,在分析星载天线的振动特性时,可视之为固支结构。

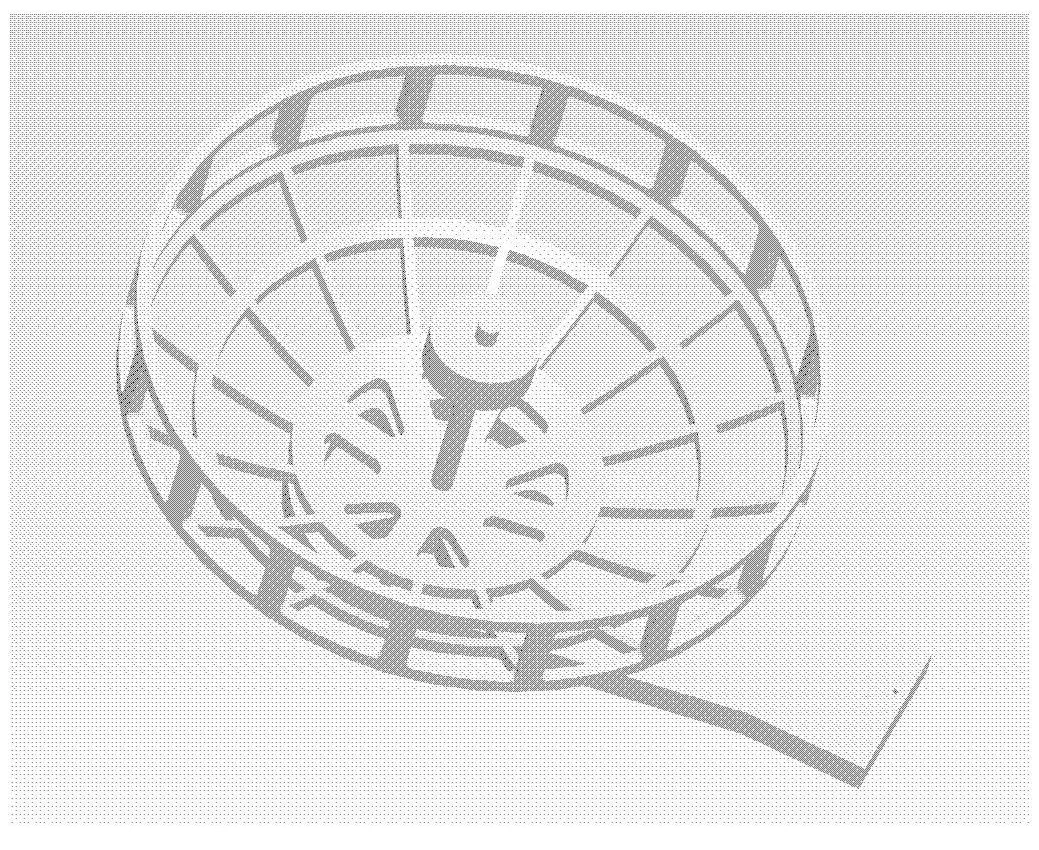
图4 天线结构Fig.4 Antenna structure

对天线结构进行模态分析,所得1～6阶的固有频率相应为11.37,14.81,21.26,21.37,28.94,29.24 Hz,其中前4阶模态振型如图5所示。

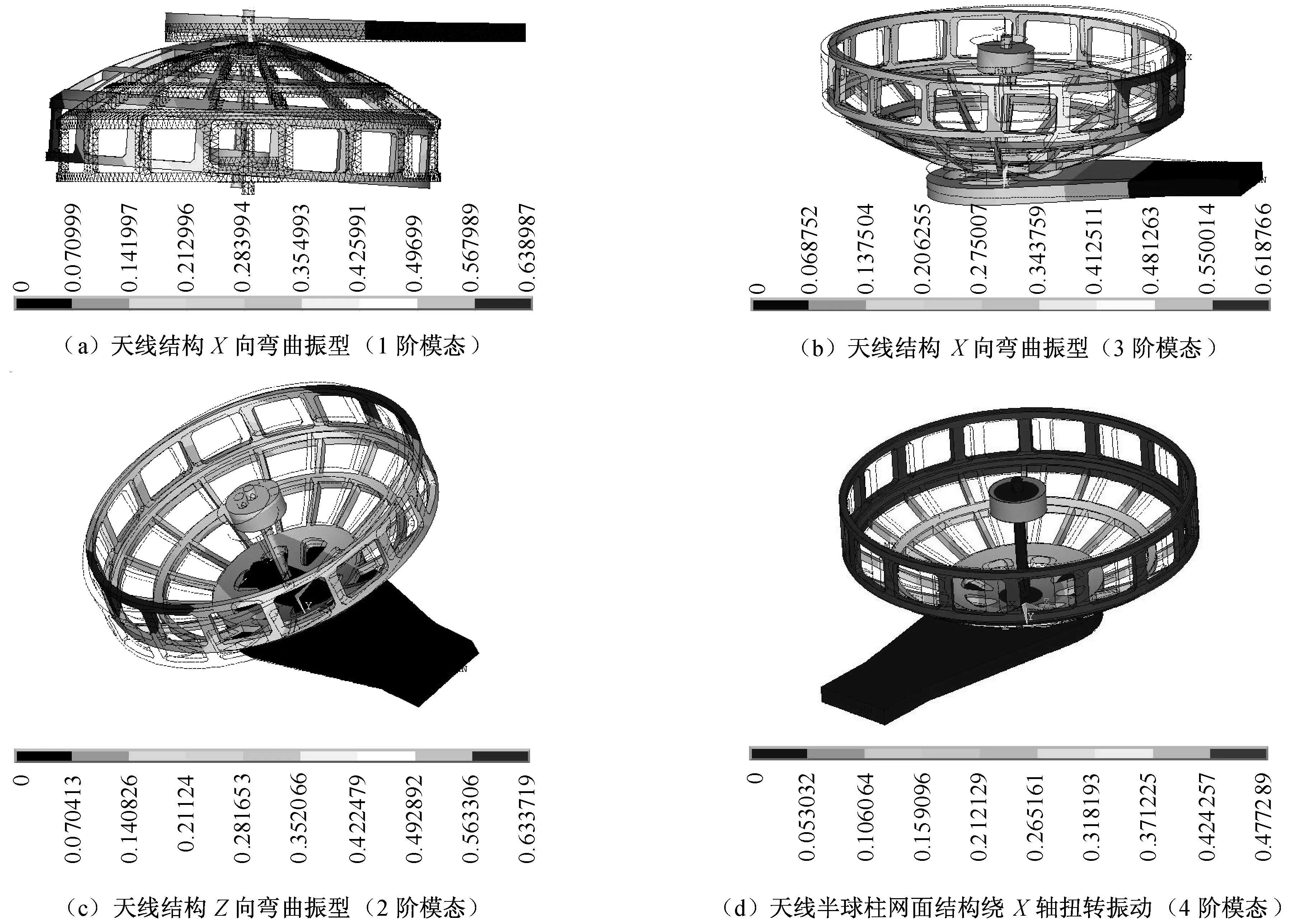
图5 天线结构1～4阶振型Fig.5 First 4 modes of antenna structure

3.2 附件振动与姿态动力学耦合算例

仍以某双自旋卫星为研究对象,建立其姿态动力学模型,其中包括姿态控制模块、球-管式章动阻尼器模块,以及喷气推力器模块等。设初始时刻,平台相对卫星质心惯性系姿态[ψ θ φ]=[0° 30° 30°],平台角速率在O-xyz系中角速率ω=[0 0 0]rad/s,输入附件天线结构的振动特性,联合仿真所得卫星本体姿态角及角速率变化分别如图6、7所示。在姿态控制系统的作用下,自旋轴方向单位矢量端点在质心惯性系中投影的变化轨迹如图8所示。

仿真结果表明：在喷气姿态控制和被动章动阻尼控制下,卫星平台姿态角趋于目标姿态角,角速率趋于零。星载天线结构作高频微幅振动,自由端最大振幅约10-6m量级,其振动响应对卫星本体的影响较小。另由图8可知：在姿态机动和附件结构振动相互耦合的影响下,卫星姿态控制系统仍能保持稳定。

图6 卫星姿态角变化过程Fig.6 Variation of satellite attitudeangle

图7 卫星角速率变化过程Fig.7 Variation of satelliteangular rate

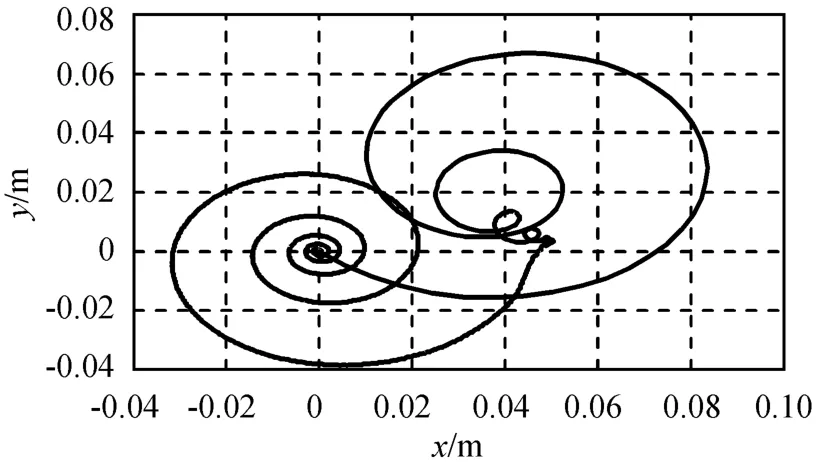
图8 自旋轴方向端点在质心惯性系中投影Fig.8 Projection with direction of spin axis on barycentric inertia coordinates

4 结束语

本文以某双自旋卫星星载天线为挠性附件,建立了基于有限元方法和刚体动力学结合的航天器姿态动力学模型,并实现了航天器结构-姿态的动力联合仿真。研究结果表明：通过此联合仿真方法能实现航天器姿态控制全系统的性能分析和评估,在工程应用中有一定的参考价值。

[1]MODI V.Attitude dynamics of satellites with flexible appendages：a brief review[J].Journal of Spacecraft and Rockets.1974(11)：743-751.

[2]曲广吉,程道生.复合柔性结构航天器动力学建模研究[J].中国工程科学,1999,1(2)：52-56.

[3]屠善澄,陈义庆.卫星姿态动力学与控制(I)[M].北京：中国宇航出版社,1999.

[4]CHOONGSEOK O H.Vibration control of flexible spacecraft under attitude maneuver using adaptive controller[C]//AIAA Guidance.Navigation and control Conference and Exhibit.Keystone,CO：AIAA,2006-6182：1-20.

[5]蒋建平,李东旭.带挠性附件航天器刚柔耦合动力学[J].上海航天,2005,22(5)：24-27.

[6]王勖成.有限单元法[M].北京：清华大学出版社,2005.