基于CMM的线轮廓度误差测量与评定技术*

路 坦,高 雷,安 涛,桂贵生

(1.合肥工业大学机械与汽车工程学院,合肥 230009；2.马钢股份有限公司车轮轮毂公司,安徽马鞍山 243021)

基于CMM的线轮廓度误差测量与评定技术*

路 坦1,高 雷1,安 涛2,桂贵生1

(1.合肥工业大学机械与汽车工程学院,合肥 230009；2.马钢股份有限公司车轮轮毂公司,安徽马鞍山 243021)

针对动车轮踏面线轮廓度误差检测,研究使用三坐标测量机检测平面线轮廓度误差的方法。以踏面轮廓CAD图形节点数据描述理论轮廓,以实际踏面轮廓探测点数据描述被测轮廓,应用最小二乘法和条件约束优化方法计算和评定线轮廓度误差。该方法的优点是分离和消除被测轮廓与理论轮廓间的位置误差对轮廓度误差评定结果的影响。

线轮廓度误差；最小二乘法；三坐标测量机

0 引言

动车轮踏面轮廓由多段直线段和圆弧段组成,难以用一个数学表达式描述,其测量基准不可能与设计基准重合,因而在计算机上按等误差法将轮廓CAD图形离散为有限个节点,将所得节点数据作为理论轮廓；在三坐标测量机上测得的有限个节点数据作为被测轮廓。由于两组节点数据是不同坐标系中的数据,求实际轮廓与理论轮廓的偏差需要调整测量坐标系位置,使实际轮廓与理论轮廓偏差符合最小条件原则。由于最小条件原则实现困难,故采用最小二乘法和条件约束优化方法调整被测轮廓的位置,将位置误差从轮廓误差中分离出去。

1 线轮廓度误差定义

根据GB/T1182——2008的定义,线轮廓度是限制实际曲线对理论曲线变动量的一项指标。按最小区域法评定原则,线轮廓度误差是指包容被测轮廓的理论轮廓等距线的最小间距。线轮廓度公差用于控制平面曲线或曲面截面轮廓的形状误差,公差带是包络一系列直径为公差值t的圆的两包络曲线之间的区域,诸圆圆心应位于理论轮廓曲线上,如图1所示。

线轮廓度误差是实际轮廓对理论轮廓的实际变动量,在量值上等于理论轮廓两侧的实际轮廓与理论轮廓的距离之和。

2 平面线轮廓数字化

2.1 理论轮廓

图2 “测量”动车轮踏面理论轮廓

2.2 实际轮廓

实际轮廓是未知的,使用三坐标测量机测量实际轮廓,测得的数据是实际轮廓上测量点的坐标值。首先在实物上建立测量坐标系(如图3所示),以O点作为坐标原点,在被测实际轮廓上划分m个节点作为测量点,得到实际轮廓m个节点坐标值(xi,yi,zi)。

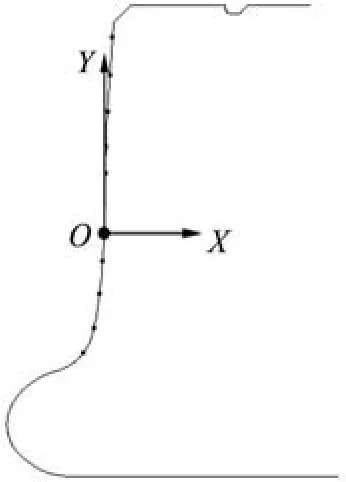
图3 测量动车轮踏面实际轮廓

理论轮廓和实际轮廓节点数据如表1所示。

表1 理论节点与实际节点坐标值

(续表)

3 理论轮廓表达式

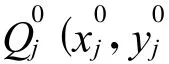
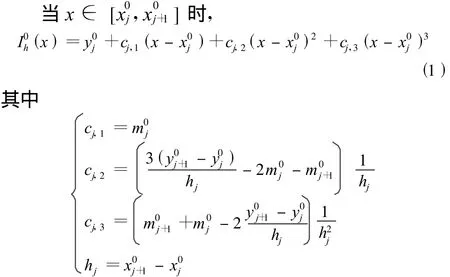
4 实际轮廓节点在理论轮廓上的投射点

所谓实际轮廓节点在理论轮廓上的投射点是指实际轮廓节点到理论轮廓曲线的垂足。投射点的计算分两步,先确定投射点位于哪一段曲线上,继而计算投射点的坐标。

4.1 确定投射点在理论轮廓曲线上的区间

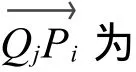
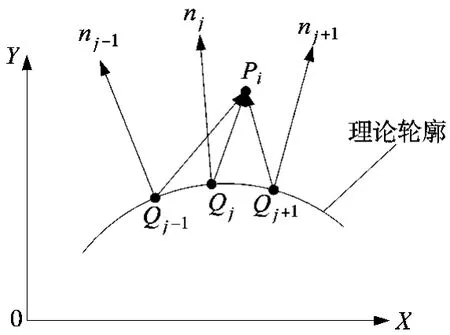
图4 实际轮廓节点在理论轮廓线上的投射区间

4.2 计算投射点的坐标

在测量坐标系X-Y中,实际轮廓节点Pi(xi,yi)到理论轮廓(x)之间的偏差为di(i=0,1,…,n),偏差di为Pi(xi,yi)到(x)的法向最小距离,公式为:

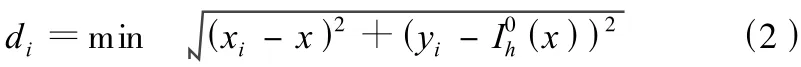
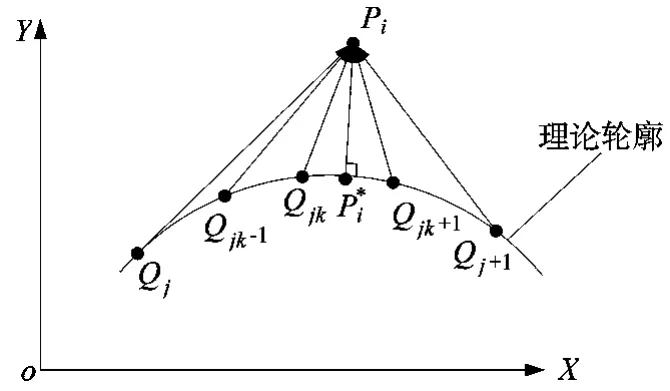
图5 实际轮廓节点到理论轮廓曲线的距离

(1)将第j段曲线按等间距法沿参数x方向细分成s段,计算给定点Pi(xi,yi)到各个细分点Qjk(k=1,2,…,s-1)之间的距离 djk；

(2)求所有距离的最小值,即dmin=min{dj1,dj2,…,djk,…djs-1}；

(3)若djk是最小值,则计算djk-1和djk+1,的差值Δ =|djk+1-djk-1|,若 Δ小于或等于优化精度 δ,则dmin就是所求的给定点到曲线的最小距离,对应的Qjk点就是实际点Pi在理论轮廓曲线上的投射点P；若 Δ ＞δ,则继续迭代,直至 Δ≤ δ,求得投射点P。

5 轮廓度误差的评定

由于实际轮廓节点数据和理论轮廓节点数据是不同坐标系中的数据,求实际轮廓与理论轮廓的偏差需要调整测量坐标系位置,使实际轮廓与理论轮廓偏差符合最小条件原则。由于最小条件原则实现困难,故采用最小二乘法和条件约束优化方法调整被测轮廓的位置,将位置误差从轮廓误差中分离出去。

轮廓度误差的评定算法以实际轮廓节点Pi(i=0,1,…,n)到理论轮廓的偏差di的平方和最小为准则来调整实际轮廓节点在理论坐标系X0-Y0下的位置,使实际轮廓最大限度地适应理论轮廓。设测量坐标系X-Y在理论坐标系X0-Y0下的位置为(u,v,θ),其中(u,v)为 X 、Y轴的坐标平移量,θ为坐标旋转量。将测量坐标系X-Y下的实际轮廓节点Pi(xi,yi)转换到理论坐标系X0-Y0下节点Pi′(xi′,yi′),依据坐标系变换关系有:

节点 Pi′(xi′,yi′)在Pi(xi,yi)的邻域内,故点Pi′(xi′,yi′)在理论轮廓上的的投射点可用Pi(xi,yi)的投射点P*i近似代替。

根据最小二乘法原理建立计算u,v,θ的数学模型:

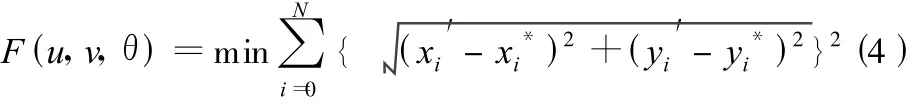
这是一个典型的三维优化问题,采用加速步长的坐标轮换法对(4)式表达的优化模型求解,给定初始设计参数(u0,v0,θ0)T；初始寻优化步长(hu,hv,hθ)T以及收敛判别系数E；以理论节点P(j=0,1,…,m)为原始数据拟合曲线(x)；求得各测点Pi′与理论轮廓(x)之间的偏差d,当Pi′在(x)上方时d为正,反之为负；计算

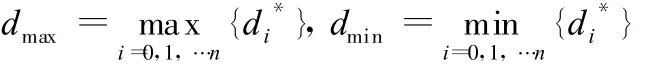
根据轮廓误差的定义,轮廓度误差为F=dmax-dmin。

6 结束语

以动车轮踏面的测量数据为例,算得轮廓度误差F=0.1413mm,其中(u,v,θ)={0.0064,0.0026,0.0011}；三坐标测量机测得轮廓度误差 F =0.1496mm。

用本文提出的线轮廓度误差评定方法评定动车轮踏面线轮廓误差,所得结果与某型号三坐标测量机的检测结果几乎相同,证明了本文提出的线轮廓度误差评定方法是可行的。

[1]熊有伦.精密测量的数学方法[M].北京:中国计量出版社,1989.

[2]刘文文,聂恒敬.一种自适应的平面线轮廓度误差评定方法[J].计量学报,1999(1):27-31.

[3]苑国英.用于坐标测量机上测量形位误差的软件包[J].现代计量测试,1994(4):23-26.

[4]戴能云,廖平,王建录,等.基于MATLAB的平面线轮廓度误差评定[J].计算机测量与控制,2010,18(7):1590-1592.

[5]廖平.分割逼近法快速求解点到复杂平面曲线最小距离[J].计算机工程与应用,2009,45(10):163-164.

[6]郭慧,马永有,潘家祯.基于遗传算法的复杂平面曲线轮廓度误差评定[J].华东理工大学学报(自然科学版),2007,33(6):888-892.

[7]杨密,李平,卢春霞,等.复杂平面曲线轮廓度的评定[J].工具技术,2006,40:76-79.

[8]王伯平,景大英.一种评定平面线轮廓度误差的新方法[J].太原重型机械学院学报,2005,26(1):46-50.

[9]王林艳,王建华.基于坐标法的复杂曲面轮廓度的误差评定[J].西安工业学院学报,2006,26(3):228-232.

[10]苑国英,冯文澜,邱志慧.在坐标测量机上检测复杂曲面形状误差的理论与方法研究[J].工程设计,2000(4):75-77.

Measurement and Evaluation Technology of Plane Profile Error Based CMM

LU Tan1,GAO Lei1,AN Tao2,GUI Gui-sheng1
(1.School of Machinery and Automobile Engineering,Hefei university of technology,Hefei 230009,China；2.Wheel and Type Plant of Maanshan Iron＆Steel Co.Ltd.,Maanshan Anhui 243021,China)

Aiming to the measuring of profile of a line error r of high speed wheel tread,work over the profile of a line error measuring method by CMM.For the CAD figure node data of profile of tread line being profile in frame of reference,for the measuring node data of profile of tread line being measuring profile,using east square method and conditional optimizative method to evaluate profile of a line error.The excellence of this method is to apart and remove position error between profile in frame of reference and measuring profile to make the result being more exactitude.

profile of a line error；least square method；CMM(Coordinate Measuring Machine)

TH16；TG65

A

1001-2265(2011)10-0075-03

2011-03-03

国家863高技术研究发展计划重点课题(2008AA030703)

路坦(1988—),男,安徽巢湖人,合肥工业大学机械与汽车工程学院硕士,研究方向为先进制造及特种加工,(E-mail)375576658@qq.com。

(编辑 李秀敏)