细长轴切削的非线性系统动力稳定性分析*

丛春晓,刘 恒,吕凯波,景敏卿

(西安交通大学机械电子及信息系统研究所,西安 710049)

细长轴切削的非线性系统动力稳定性分析*

丛春晓,刘 恒,吕凯波,景敏卿

(西安交通大学机械电子及信息系统研究所,西安 710049)

为了研究细长轴切削过程中的振动特征以及稳定性,运用轴承转子非线性分析理论研究非线性滚动轴承力和非线性切削力作用下的系统稳定性及失稳分叉规律。建立了非线性切削力模型和细长轴的有限元分析模型。通过周期解、Poincaré截面映射图确定系统的运动特性。经过计算,系统的失稳分叉方式是同步周期解经Hopf型伪周期分叉产生伪周期解。与空转情况相比,切削状态下的细长轴分叉点转速下降近80%,且其分叉点转速范围较窄。在系统参数中,稳定性规律对转轴长径比和轴承刚度的变化比较敏感。通过双主轴驱动的细长轴切削实验可以得出,失稳前后系统的频率变化特征和运动形态与计算结果一致。为提高切削稳定性,失稳颤振的预测和监测提供理论依据。

细长轴；非线性动力特性；稳定性；分叉

0 引言

在车削轴类零件的过程中,动态切削力和振动位移会相互耦合形成自激振动。当切削轴刚度较大时,系统的切削稳定性主要取决于刀具,可以把轴当作刚体。由于细长轴的柔性较大,在切削力的作用下容易激起振动,加工质量难以保证,所以其加工稳定性一直是学者们的研究对象。并且目前的车刀刚性也较大,所以细长轴的结构振动对切削稳定性的影响不能忽视。以前一般把细长轴当成刚支简化梁来进行研究,赵海涛[1]建立了细长轴车削时的简化受力模型,并在此基础上对细长轴的振动作了理论研究。随着转子动力学的发展成熟,柔性转子的研究成果应用于对切削振动的分析上,邹亚平[2]利用转子动力学的方法对切削振动进行了研究,考虑了不同参数对振动的影响。在解析法稳定性分析中,由于分析方法的限制,轴承力和切削力多简化为线性力[3]。为了研究切削系统的非线性动力特性,通过建立非线性模型,对转子进行有限元离散的数值分析方法可以对非线性动力系统进行稳定性分析。TIWARI[4]建立了非线性滚动轴承支承的转子模型。张伟刚[5]等建立了6自由度的机床主轴-滚动轴承系统,进行非线性动力学研究。J.-J.SINOU[6]用Timoshenko梁轴单元对轴承——转子系统进行了有限元建模,并研究了非线性滚动轴承力对系统稳定性的影响。

结合双电主轴驱动的车削机床(图1)的结构特点,本文将细长轴的切削系统简化成滚动轴承支承的柔性转子。将轴承-转子非线性动力系统的稳定性和分叉理论运用到对细长轴切削加工稳定性的分析上。研究该柔性转子在非线性轴承力和非线性切削力作用下的振动特性。求出切削加工前后的自激振动失稳转速以及失稳形式。并研究了轴承接触刚度系数、长径比对稳定性分叉规律的影响。最后通过在车铣复合中心上的细长轴车削实验,将实验数据与理论计算结果进行验证。为切削参数的确定,失稳颤振的预测和监测提供理论依据。

图1 双电主轴车削机床

1 切削力和滚动轴承力的非线性分析模型

1.1切削力模型

在切削过程中,工件的振动位移会通过切削厚度的改变来影响切削力,产生动态切削力,形成自激效应。为了对切削系统进行振动特性研究,需要确定非线性动态切削力分析模型,建立如图2所示的轴类零件切削力模型。

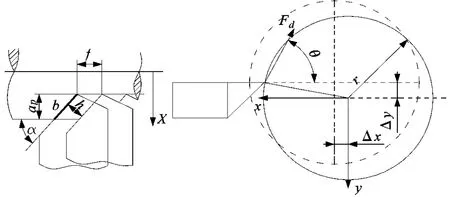
图2 轴类零件切削力模型

设在切削过程中轴心的振动位移为x,y,则

由于振动产生的切削深度变化量为

瞬时切削深度ap=ap′+Δ ap,ap′为理论切削深度(mm),r为轴的半径。

切削宽度b=ap/sinα,α为刀具主偏角。

切削厚度 h=f⋅sin α+Δ ap⋅cosα,f为理论轴向进给量(mm/r)。

动态切削力为:

Kd为切削力系数(N/mm2)[7]。

1.2 角接触球轴承的支承力模型

在加工机床中,主轴的支承多为角接触球轴承。根据赫兹弹性接触理论,第j个滚动体与滚道间的局部接触力Qj与弹性变形 δj之间的关系可表示为[4]:

其中Kn为单个滚珠的接触刚度系数(N/mm1.5)。

角接触轴承轴向预紧后,第j个滚动体的弹性变形表示为:

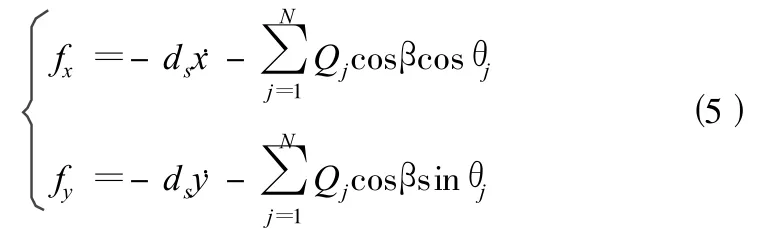
式中ds为接触阻尼,其大小和等效刚度系数的关系为:

dk为轴承阻尼系数(0.25 ×10-5～2.5 ×10-5)[8]。

2 非线性动力系统稳定性分析

2.1 稳定性分叉规律的数值分析方法

为了对非线性系统进行数值法稳定性分析,采用Timoshenko梁轴有限元单元[9]对转子系统进行离散。由于非线性特征在轴承和切削点的区域,所以系统属于高维局部非线性系统,为了保证完整分析整个系统的动态特性,同时减小计算量,采用模态综合法将非线性节点自由度保留在物理空间,将线性部分转化到模态空间,实现系统降维[10]。

获取缩减后的系统质量、阻尼和刚度矩阵后,建立系统运动方程:

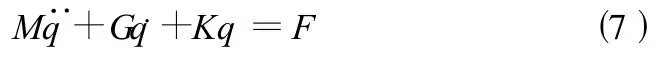
其中F=Fg+Fb+Fex+Fc；Fg为重力向量,Fb为轴承力向量,Fex为不平衡外激励力向量,Fc为非线性切削力向量。

研究非线性动力系统稳态周期解随外参数变化的分叉规律,用打靶法求解系统的周期解,然后用CPNF(Continued-Poincar é-Newton-Floquet)[11]方法追踪预估外参数变化时的周期解。对非线性动力系统的周期解的判稳以及分叉形式通过对周期解的状态转移矩阵的特征值(Floquet乘子)的结构分析得出[12]。

结合以上理论,建立如图3所示的细长轴切削模型,其中细长轴分成8段,整个转子分成10段,共11个节点,其中非线性滚动轴承力加在2和10节点上。自由度缩减时保留3个节点(轴承2和10,切削点6),保留8阶低阶模态。

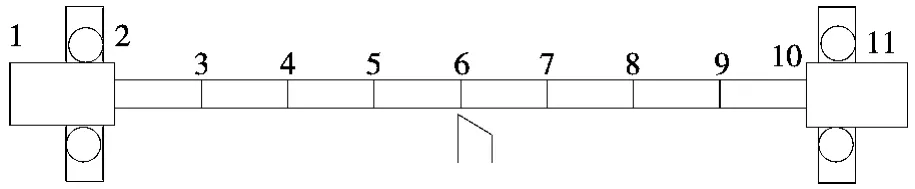
图3 轴承转子有限元模型

2.2 无切削力时的e-ω图

在不加切削力的情况下,细长轴受非线性轴承力和轴段质量偏心的影响,取细长轴长度320mm,轴径20mm,轴承刚度系数Kn=5.465 ×1010N/m1.5,经过计算可得分叉点转速随质量偏心变化的e-ω图如图4a所示。

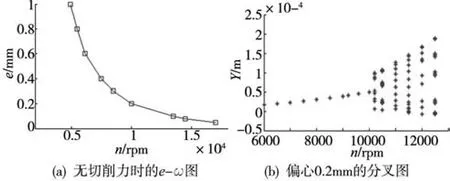
图4 转速变化图

从图中可以看出,不加切削力时转子系统的分叉点转速在5000 ～20000rpm区域内,取出细长轴的质量偏心为0.2mm的一组参数进行研究,其振动位移随转速变化的分叉图如图4b所示。转速从9000rpm到11000rpm之间的Floquet乘子的变化规律如表1所示。

表1 无切削力时Floquet乘子 λ的变化

可见转速经过10000rpm时,有一对Floquet乘子以复共轭方式穿出复平面上的单位圆,同步周期解经Hopf型伪周期分叉产生伪周期解,在分叉点前后各取一点研究其特性,当转速9000rpm时,节点6的同步周期解以及细长轴各节点的解如图5所示,当转速为11000rpm时,节点2和节点6的伪周期解以及其在Poincar é截面上的投影如图6所示。

图5 转速9000rpm时节点6的同步周期解和细长轴运动

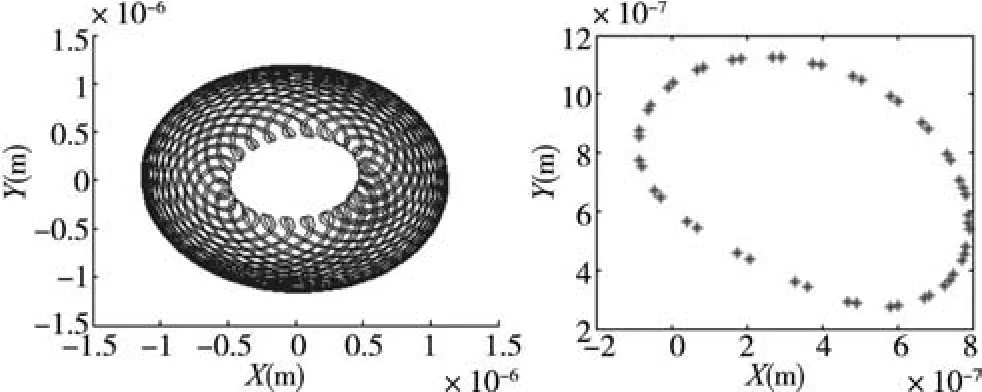
图6 转速11000rpm时节点2的伪周期解和Poincaré maps

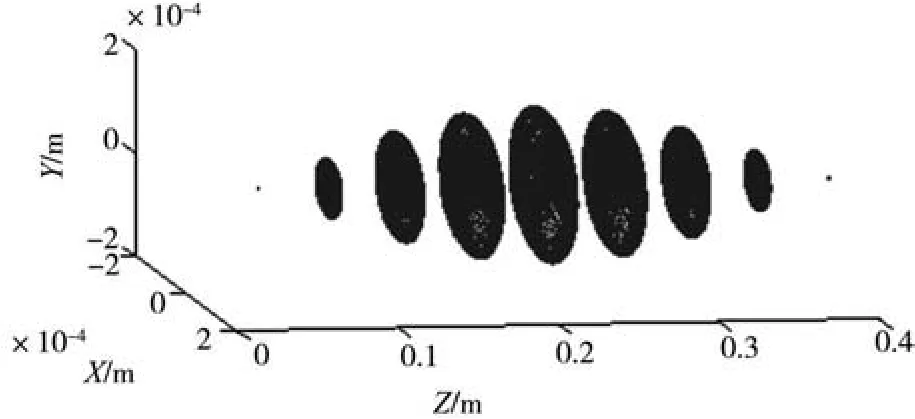
图7 转速11000rpm时细长轴的伪周期运动

2.3 加上动态切削力时的e-ω分叉规律

为了考虑在加工状态下质量偏心的不同对稳定性的影响,给定切深ap=0.5mm,则系统的e-ω图如图8所示。

图8 切深0.5mm时的e-ω图和偏心0.2mm的分叉图

从图中可知,系统的分叉点转速在2050 ～2130rpm区域内,在100rpm以内,与无切削力时相比,分叉点转速的变化范围很小,可见切削过程中系统的分叉点对质量偏心的变化比较不敏感。同样取出细长轴的质量偏心为0.2mm的一组参数进行研究。其转速从1800rpm到2200rpm之间的Floquet乘子的变化规律如表2所示。

表2 切削深度0.5mm时Floquet乘子的变化

转速经过2129rpm时,同步周期解经Hopf型伪周期分叉产生伪周期解。当转速2000时,节点6的同步周期解,Poincar é截面图以及细长轴各节点的解如图9,10所示。转速2200时,节点2和节点6的伪周期解以及其Poincar é截面图如图11所示。

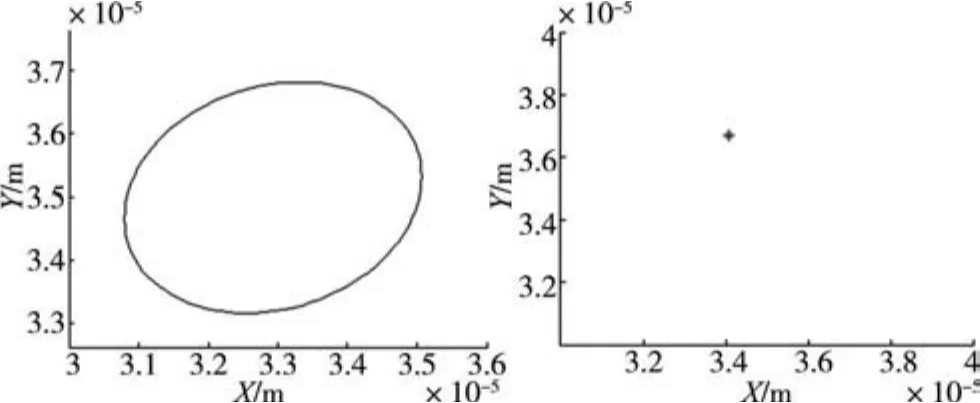
图9 转速2000rpm节点6的同步周期解和Poincaré maps

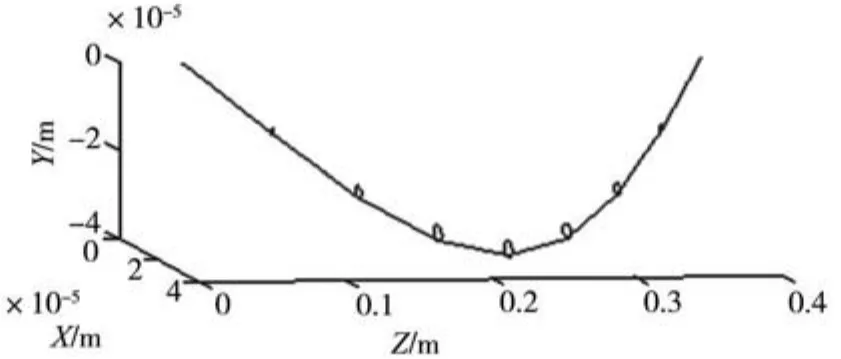
图10 转速2000rpm时细长轴的运动情况

通过与上图的对比可以发现,空转时转子的运动是以靠近原点处为中心的同步周期运动,其稳定振动的幅值较大。切削状态下转子的运动中心偏离原点较大,而其稳定振动幅值较小。

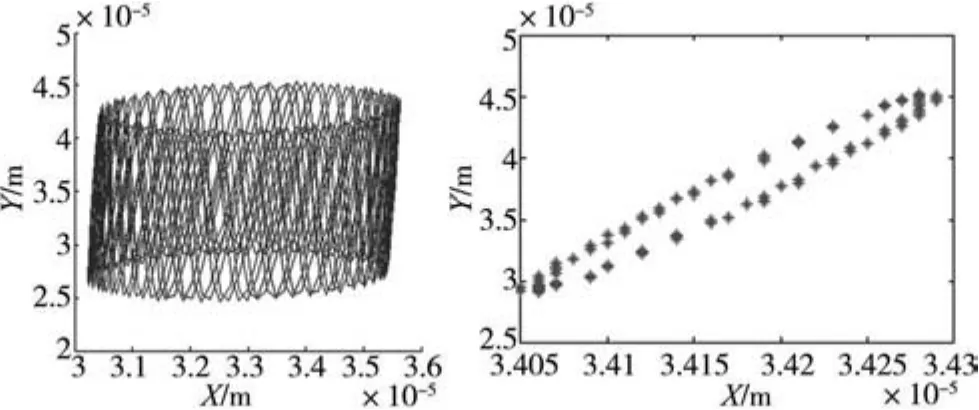
图11 转速2200rpm节点6的伪周期解和Poincaré maps

由以上结果可得,与空转情况相比,切削状态下的细长轴分叉点转速大幅下降,由10000rpm附近降到2100rpm附近,降幅近80%,且其分叉点转速范围较窄。两种情况下的失稳分叉方式都是同步周期解经Hopf型伪周期分叉产生伪周期解。

3 实验分析和验证

通过数值方法的计算,可以确定非线性切削系统的失稳频率特征和运动特征。为了验证计算结果,设计双主轴驱动的细长轴切削实验,实验在车铣复合中心(CHD25A)上进行,实验方案如图12所示,实验参数和设备类型如表3所示。在实验中通过改变切削参数,采集系统稳定切削和不稳定切削两种状态下的数据。通过频域分析和轴心轨迹对切削轴的振动进行研究,分析数据并与计算结果进行对比。

表3 实验参数和设备

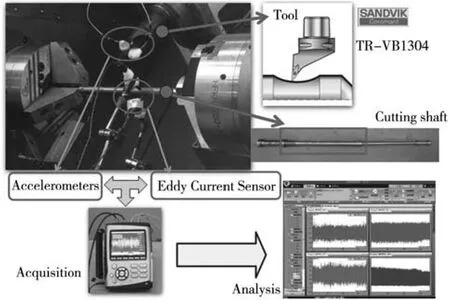
图12 车铣复合中心和实验方案

从图13～14中的实验结果可以看出在稳定切削时,细长轴的加工表面比较光滑,振动较为平稳,通过频率分析可以看出,振动频率以工频为主。通过数值计算可得,切削系统失稳以前的运动形式为同步周期解(图15,图中w为系统振动频率,w1为工作频率),振动频率为工频(w/w1=1),计算结果与实验数据一致。

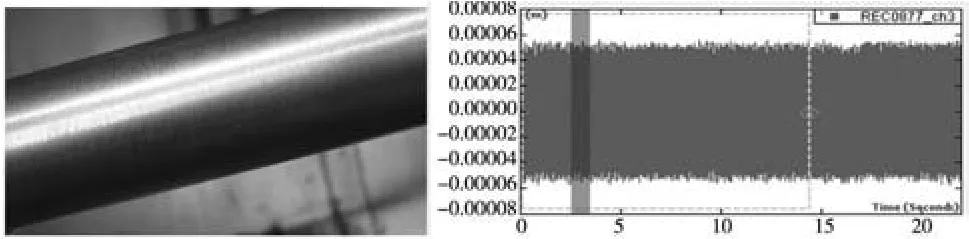
图13 稳定切削时的表面质量和轴件的时域波形

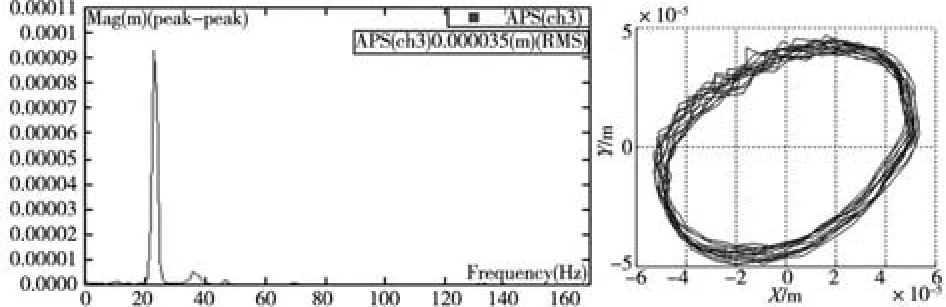
图14 稳定切削时的主频率和轴心轨迹

图15 计算得到的稳定振动主频率和同步周期解

当切削深度等参数改变,系统可能发生失稳颤振,从图16 ～17中可以看出,细长轴加工表面粗糙,系统的振动位移较大,系统的主频率发生变化,以3倍频为主,且运动轨迹较为混乱。不易满足加工表面质量的要求。数值计算结果显示(图18),系统发生失稳的形式为同步周期解分叉形成伪周期运动,伪周期运动的主频率为3倍频(w/w1=3)。实验结果和计算结果也相一致。

图16 切削失稳时的表面质量和时域波形

图17 切削失稳主频率和轴心轨迹

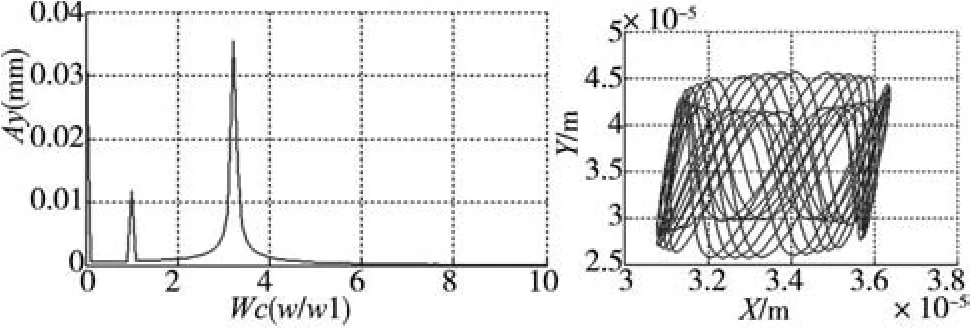
图18 通过计算的伪周期主频率和运动轨迹

4 系统参数的改变对稳定性分叉集的影响

4.1 细长轴长径比变化的影响

在细长轴的加工中,对转轴长径比比较敏感,长径比越大,转轴柔性越大,越难加工。设轴径不变,可以通过改变细长轴的长度来研究细长轴在不同长径比情况下的分叉规律,参数Kn=1.095×1010N/m1.5,转轴直径20mm,取切削深度0.5mm,分别取长度400mm,360mm,320mm(长径比分别为20,18,16)三组细长轴进行研究,其稳定性分叉规律如图19所示,其中纵坐标为切削宽度,横坐标为转速。

图19 细长轴的长径比变化对分叉集的影响

从图中可以看出细长轴长度越小,其分叉点转速越高,切深0.5mm时三组长径比的分叉点分别为2763rpm,4200rpm,5639rpm,可见当转轴长径比由16增加到20,分叉点转速减小了51%。从图中还可以看出,分叉曲线不是单调的,不是切深越小越稳定,理想的切削深度都在0.5mm左右。所以在加工过程中应尽量减小加工部分的长度并合理的调整切削深度。

4.2 轴承刚度系数变化的影响

在机床加工过程中,主轴的旋转特性对加工有很大影响,机床主轴多采用角接触球轴承支承,轴承安装方式以及预紧状态的差异都对转子系统的稳定性造成影响。预紧状态的不同可以导致角接触球轴承的接触刚度不同,取三组不同的接触刚度系数,研究轴承接触刚度系数对稳定性分叉规律的影响。如图20所示,可以分析得出,在不考虑旋转精度的情况下,接触刚度系数越小,分叉转速越大,稳定区域越大。图21为接触刚度不同时节点2的周期解情况,可以看出,接触刚度系数越小,周期解的振幅越大,旋转精度越差。因此需要考虑稳定性和加工质量的双重因素来适当的调整轴承的刚度系数。

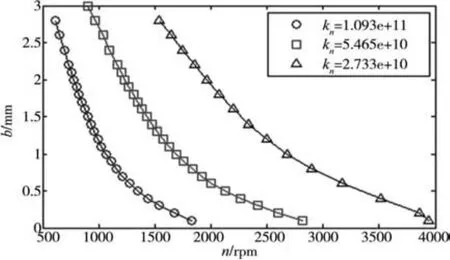
图20 轴承接触刚度系数对稳定性分叉规律的影响

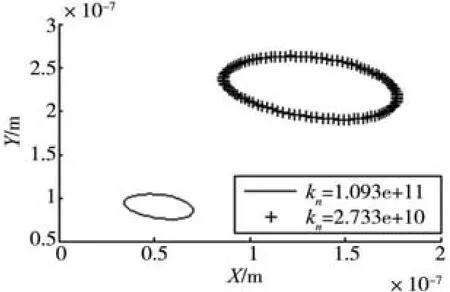
图21 轴承接触刚度系数对旋转精度的影响

5 结束语

(1)建立了细长轴的非线性有限元分析模型进行稳定性分析。与空转情况相比,切削状态下的细长轴分叉点转速大幅下降,降幅近80%,且其分叉点转速范围较窄。两种情况下的失稳分叉方式都是同步周期解经Hopf型伪周期分叉产生伪周期解。

(2)通过进行细长轴的切削实验发现,系统失稳前后的振动特征在时域上和频域上都与理论分析相一致。稳定切削是工频为主的同步周期运动,失稳切削是以3倍频为主的伪周期运动。失稳后的表现形式为振幅的增大和振动主频率的转变,为失稳颤振的预测和监测提供理论依据。

(3)稳定性规律对转轴长径比和轴承刚度系数比较敏感。减小长径比能大幅度的提高系统的加工稳定性。理想的切削深度在0.5mm左右。轴承接触刚度系数越小,稳定区域越大而旋转精度越差,提高稳定性需要适当的调整轴承的刚度系数。

[1]赵海涛,杨建国,童恒超.细长轴车削加工的振动及其补偿控制[J].上海交通大学学报,2005,39(1):117-120.

[2]邹亚平.基于转子动力学的车削颤振模型建立及其动态特性分析[D].大连:大连理工大学,2009.

[3]HAMED.MORADI,M.R.MOVAHHEDY,G.REZA VOSSOUGHI.Robust control strategy for suppression of regenerative chatter in turning[J]. Journal of Manufacturing Processes,2009,11:55-65.

[4]M.TIWARI,K.GUPTA.Effect of radial internal clearance of a ball bearing on the dynamics of a balanced horizontal rotor[J].Journal of Sound and Vibration,2000,238:723-756.

[5]张伟刚,高尚晗,龙新华,等.机床主轴-滚动轴承系统非线性动力学分析[J].振动与冲击,2008,27(9):72-75.

[6]J.-J.SINOU.Non-linear dynamics and contacts of an unbalanced flexible rotor supported on ball bearings[J].Mechanism and Machine Theory,2009,44:1713-1732.

[7]EMRE OZLU,ERHAN BUDAK.Analytical Modeling of Chatter Stability in Turning and Boring Operations-PartII:Experimental Verification[J].Manufacturing Science and Engineering,2007,129:726-732.

[8]S.P.HARSHA,K.SANDEEP,R.PRAKASH.The effect of speed of balanced rotor on nonlinear vibrations associated with ball bearings[J].Mechanical sciences,2003,45:725-740.

[9]NELSON H D.A finite rotating shaft element using Timoshenko beam theory[J].ASME Journal of Mechanical Design,1980,102(4):793-804.

[10]HO Y S,LIU H,YU L.Effect of thrust magnetic bearing on stability and bifurcation of a flexible rotor active magnetic bearing system[J].ASME Journal of Vibration and A-coustics,2003,125(3):307-316.

[11]SUNDARARAJAN P,NOAH S T.Dynamics of forced nonlinear systems using shooting/arc length continuation method-application to rotor system[J].Journal of Vibration and Acoustics,1997,119(1):10-20.

[12]吕延军,虞烈,刘恒.非线性轴承-转子系统的稳定性和分岔[J].机械工程学报,2004,40(10):62-67.

Nonlinear Dynamics Stability Analysis of Cutting a Slender Shaft

CONG Chun-xiao,LIU Heng,LU Kai-bo,JING Min-qing
(Institute of Mechatronics and Information Systems,Xi'an Jiaotong University,Xi'an 710049,China)

To study the vibration characteristics and stability while cutting a slender shaft,the system's stability and bifurcation are researched under the effect of the nonlinear ball bearing force and the cutting force using the nonlinear dynamics analysis theory of rotor bearing system.The nonlinear cutting force model and finite element analysis model of slender shaft are established.The system's motion characteristics are determined by the periodic solution and Poincar émaps.The analysis result shows that system's instability bifurcate way is the synchronized periodic solution turn into quasi-periodic solution through Hopf quasi-periodic bifurcation.The speed of bifurcation point in cutting condition is reduced by 80%compared to no cutting system,and the speed has small change.Stability rules are more sensitive to the stiffness on bearings and length-diameter ratio changes on shaft.The frequency and motion characteristics in stable and unstable experiments agree well with the theory results.Which provides the theory basis for prediction and monitoring of chatter.

slender shaft；nonlinear dynamics characteristic；stability；bifurcation

TG519.1；O347.6

A

1001-2265(2011)10-0040-05

2011-02-23；

2011-04-11

国家机床重大科技专项(2009ZX04001-071)；国家自然科学基金面上项目(51075315)；轴研所主轴项目(2010ZX04012-014)；国家973计划项目(2007CB707705)；国家863计划项目(2007AA04Z432)

丛春晓(1985—),男,山东烟台人,西安交通大学机电信息研究所研究生,主要从事机床的加工振动研究,(E-mail)cong.chun@stu.xjtu.edu.cn。

(编辑 赵蓉)