齐次线性方程组基础解系的求法
韩新社
(武汉船舶职业技术学院公共课部,湖北武汉 430050)
1 引言
线性方程组是线性代数课程中一项重要内容,齐次线性方程组的基础解系,不仅对解方程本身是不可缺少的,且它在其它方面,特别是在矩阵的秩方面也有广泛的应用。对学生而言,矩阵的秩是一个难点。对于一个初学者来说,判断方程组是否有非零解是没问题的,但是想能正确而又快速的找到它的基础解系却并不容易。针对这个问题,我们下面给出求基础解系的一个简单方法,以及寻找过程中的注意事项。
齐次线性方程组是指
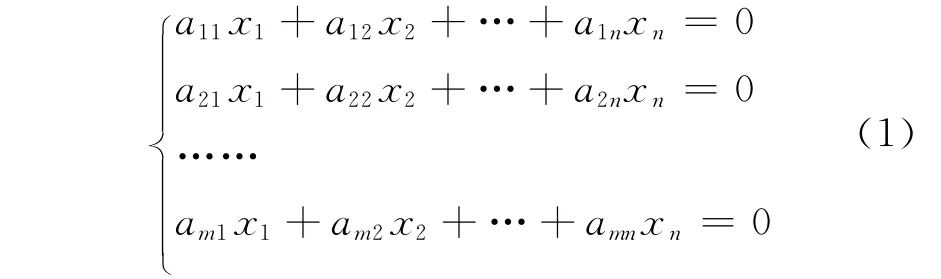
其矩阵形式为AX=0
其中A=(aij)mxn为方程组(1)的系数矩阵,X=(x1,x2,…xn)T。
我们知道,求齐次线性方程组的基础解系通常都是先对系数矩阵A进行初等行变换化成行简化阶梯形矩阵,看方程组是否有无穷多个解。若有,写出方程组(1)的含有n—r(r=秩 A)个自由未知量的一般解,然后通过给自由未知量赋值得到方程组(1)的n—r个线性无关的解向量,即为方程组(1)的一个基础解系。
本文利用矩阵的初等行变换给出了求齐次线性方程组基础解系的一种比较简便实用方法,使基础解系隐含在一个矩阵之中。
2 主要结论
定义l若矩阵C满足下列两个条件
1)C的非零行全在C的上方,零行全在C的下方;
2)非零行的第一个非零元素(称为首非零元)的列标随行标的增大而严格增大;则称C为阶梯形矩阵。
定义2设D为阶梯形矩阵,若矩阵D满足下列两个条件
1)D的非零行的首非零元均为1;
2)首非零元所在列的其余元素均为零;则称矩阵D为行简化阶梯形矩阵。
引理l[1][2][3]设 A是 mxn矩阵,若矩阵A经若干次初等行变换化为矩阵B,则存在m阶可逆矩阵P,使得
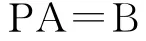
定理1设A是方程组(1)的系数矩阵,且秩A=r,若

其中Cr,m为阶梯型矩阵,且秩C=r。则Dn-r,n中的n-r个行向量α1,α2…,αn-r就是方程组(1)的一个基础解系。
证明 由引理1,存在n阶可逆矩阵P,使得

因为 P可逆,由(4)式知 Dn-r,n是行满秩矩阵,即Dn-r,n的行向量αi(i=1,2,…,n-r)线性无关。将(4)式代入(3)式得

由(7)式知(Dn-r,n)T的列向量,即Dn-r,n的行向量αi(i=1,2,…,n-r)就是方程组(1)的解向量。
因为Dn-r,n的行向量αi(i=1,2,…,n-r)线性无关,所以α1,α2,…,αn-r就是方程组(1)的一个基础解系。
3 应用举例
例1求齐次方程组
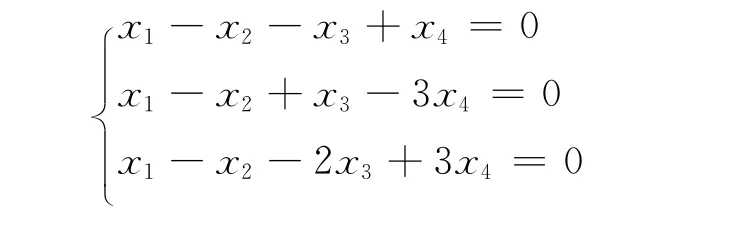
的一个基础解系。
解法1(用文献[1]-[3]的方法)
先对方程组的系数矩阵进行初等行变换,将其化为行简化阶梯形矩阵:
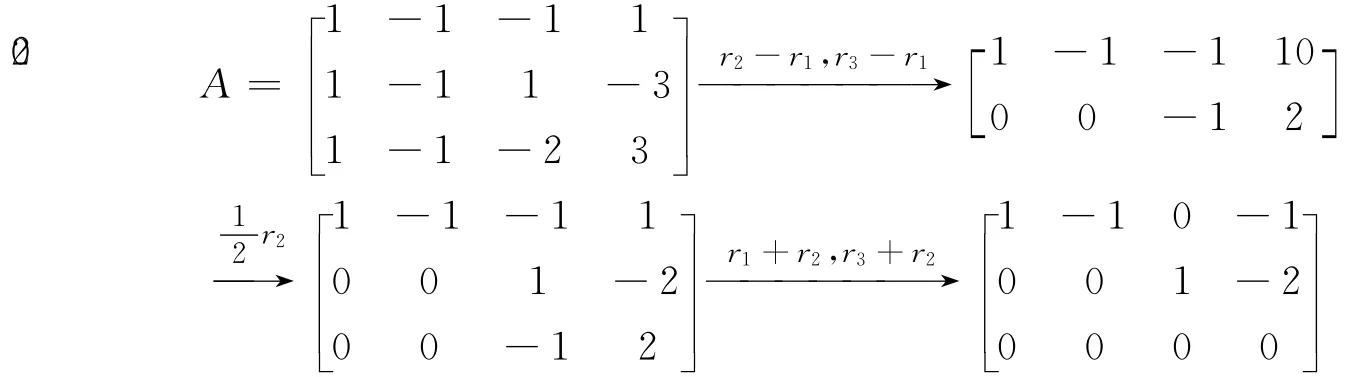
则原方程组与下面的方程组同解
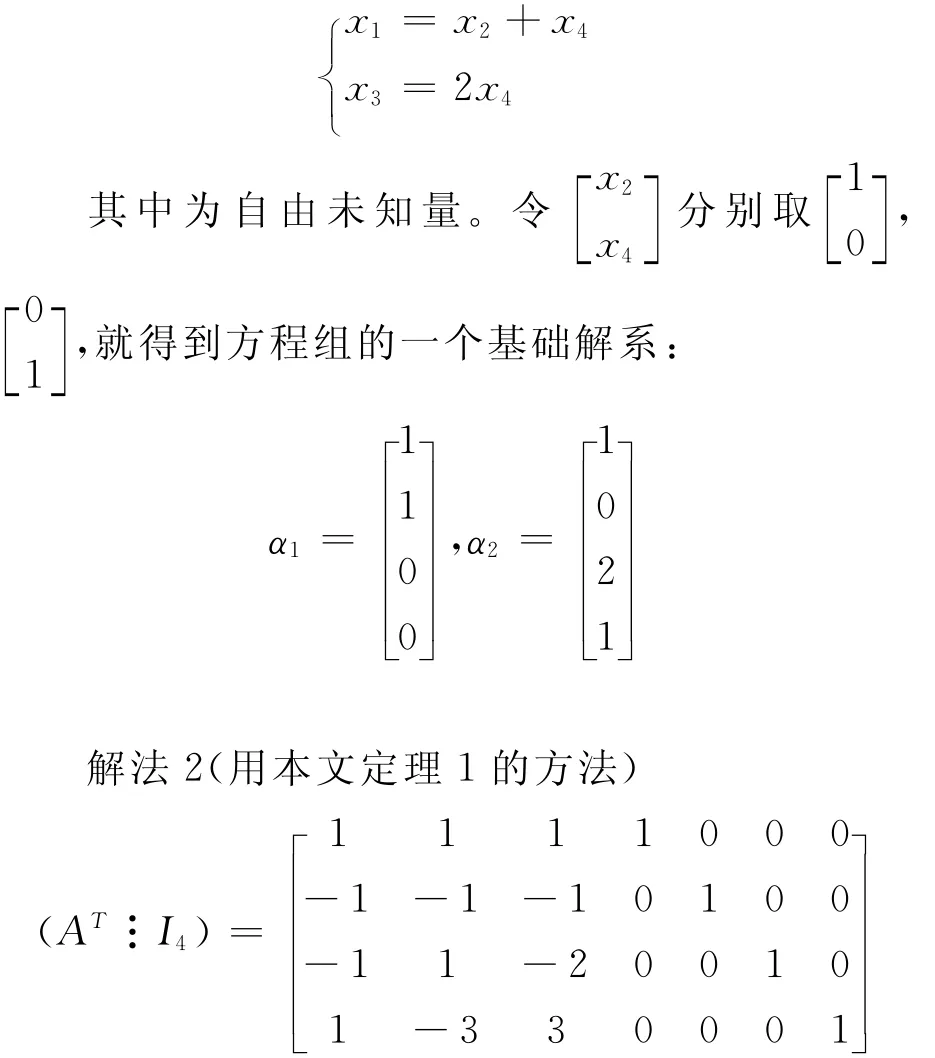

由定理1,秩 A=2。则Dn-r,n中的n-r=2个行向量α1,α2就是方程组(1)的一个基础解系:
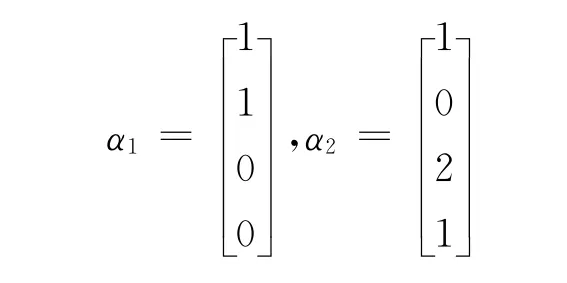
在上述两种解法中,显然解法2更为简洁。
1 北京大学数学系几何与代数教研室前代数小组编.高等代数[M].高等教育出版社,2004:140-147。
2 张禾瑞,郝炳新.高等代数(第四版)[M].北京:高等教育出版社,1999:255-261,194-195。
3 刘仲奎,杨永保.高等代数[M].北京:高等教育出版社,2003:272-277,79-80。
4 刘树利等.计算机数学基础[M].北京:高等教育出版社.2000:85-90。
5 陈建莉.线性方程组解法新探[J].纺织高校基础科学学报,2008,21(2):238-241。

