异步电机直接转矩控制系统的仿真研究

李绍博，李 君

（1.太原理工大学电子信息工程系，山西太原030024;2.中北大学电气工程系，山西太原 030051）

0 引言

实际应用中对电动机的要求主要有两点:（1）较高的机电能量转换效率;（2）根据生产机械的工艺要求转速实时可调。因此，电动机的调速问题一直以来是研究的热点问题。19世纪80年代至19世纪末的一段时间内理想的转速、转矩控制性能使得直流电动机在交流传动领域占重要地位，但其缺点限制了它在现代调速系统中的应用。从60年代起国外便十分重视交流电机调速技术，发达国家从20世纪80年代开始在传动领域已经用交流调速取代了直流调速［1］。

1 原理与设计

1.1 异步电动机的数学模型和坐标变换

建立数学模型之前，必须明确对于正方向的规定，如图1所示，正方向规定如下:（1）电压正方向（箭头方向，下同）为电压降低方向;（2）电流正方向为自高电位流入，低电位流出方向;（3）电阻上的电压降落正方向为电流箭头所指方向;（4）在不能区分线圈绕向的绕组中，电流正方向即代表磁势和磁链的正方向;（5）转子旋转的正方向规定为逆时针方向。

图1 三相异步电动机物理模型和正定方向规定

图1中，定子三相绕组轴线A、B、C在空间是固定的，以A轴为参考坐标轴，转子绕组轴线a、b、c随转子旋转，转子a轴和定子A轴间为电角度θ，并规定各绕组电压、电流、磁链的正方向符合电动机惯例和右手螺旋定则。

（1）电压方程。三相定子绕组的电压平衡方程为:

式中，uA，uB，uC为定子相电压的瞬时值;ua，ub，uc为转子相电压的瞬时值;iA，iB，iC为定子相电流的瞬时值;ia，ib，ic为转子相电流的瞬时值;ΨA，ΨB，ΨC，Ψa，Ψb，Ψc为各相绕组的全磁链;R1，R2分别为定子和转子绕组的电阻;p为微分算子。

（2）转矩方程。在一般情况下，电力拖动系统的运动方程是:

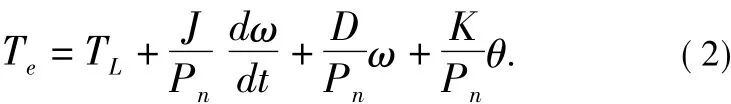
式中，TL为负载转矩;J为电动机的转动惯量;D为与转速成正比的转矩阻尼系数;K为扭转弹性转矩系数;Pn为极对数。

（3）运动方程。一般机电系统的基本运动方程式为:

1.2 直接转矩控制基本思想

所谓直接转矩控制，就是直接控制电磁转矩和定子磁链，省掉旋转坐标变换，只需定子电阻即可观测定子磁链，直接在定子坐标系下分析电动机的数学模型，控制电动机的磁链和转矩，极大解决了矢量控制方式中由于受转子参数的影响而使得系统的鲁棒性能下降的问题。它强调转矩的直接控制效果，采用离散的两点式调节器，将转矩观测值与转矩给定值作比较，使转矩波动限定在一定的误差范围之内，其结果作为产生逆变器SVPWM波形控制信号［2］。

1.3 异步电动机直接转矩控制方案分析与改进

1.3.1 直接转矩（DTC）传统控制方式的不足

DTC在实际应用中的限制主要体现在:（1）低速区定子电流和磁链的畸变非常严重，此外ω的测量误差对模型影响很大。（2）低速时转矩脉动、死区效应问题突出，上下桥臂同时导通造成直流侧短路，引入足够大的互锁延时，带来死区效应，使逆变器输出电压失真，系统运行不稳定［3］。

1.3.2 各种研究方法分析

感应电动机简洁的控制算法、直接的控制手段和优良的动、静态性能已在现代电气传动控制领域成为交流调速方案的首选，但好多方案的研究仅限于试验，且转矩脉动大和低速性能的不尽人意等问题成为制约感应电动机调速的瓶颈［4］。在定子磁链的观测环节上，观测的准确性一直是困扰DTC性能优化的首要问题［5］。另外，由于使用了六区段电压开关矢量选择表而使得常规DTC系统在区段分界线附近电磁转矩脉动过大，很大程度上制约了DTC系统的优化。采用矢量细分及优化的开关表的DTC系统可以在改善磁链增量对称性的同时，一定程度上削弱了电压矢量引起的转矩增量的不对称性，进而改善转矩控制性能。根据异步电动机DTC控制中各种不尽如人意的状况，提出的改进方案主要有:使用空间矢量脉宽调制法，改进控制参数与开关量之间的对应关系;优化磁链模型:高速时定子磁链观测U-I模型为Ψs=∫（us-isRs）dt，其误差是由定子电阻Rs的存在

而引起的。但系统中容易受到直流偏量的影响而达到积分饱和失去作用，改为Ψ=（u-iR），当速度低于

ssss30%额定转速时，us-isRs的值比较小甚至为0，致使在稳态时只有误差量被积分，使得U-I模型在低于30%额定转速，特别是低于10%额定转速时不再适用。

1.3.3 改进控制方法

影响直接转矩控制的主要问题之一便是转矩脉动过大的问题。如果通过减小滞环宽度来减小转矩脉动则会增大开关频率，与设计要求不符，转而考虑增加一个采样周期内的电压空间矢量避免单一矢量的作用。传统直接转矩控制系统为6个基本矢量组成的定子磁链轨迹，虽然各电压空间矢量与扇区相对应，但会造成编写开关表的一定困难，各个区段中作用的电压空间矢量不是很明显。本文中将扇区号与电压空间矢量号严格对应，可以简化开关表，从而加快转矩动态响应速度。现将系统改进前后的电压空间矢量对比如下:

图2 电压空间矢量设置

2 试验

仿真实验中采用鼠笼式异步电机，设定参数如下:

额定电压us=380 V，额定频率f=50 Hz，额定功率Pn=1.5 kW，定子电感Ls=0.528 4 H，转子电感Lr=0.518 8 H，定转子互感Lm=0.486 3 H，定子电阻Rs=4.85 Ω，转子电阻Rr=4.16 Ω，转子转动惯量J=0.003 98 kg·m2，极对数np=2，转矩容差为0.1 N·m，磁链容差为0.001Wb。图3为负载转矩不变，转速阶跃状态下的感应电机直接转矩控制系统仿真响应波形。我们给定负载转矩TL=5 N·m，电机转速在t=0.5 s时由1 000 r/min阶跃至50 r/min，在t=1.0 s时，电机转速由50 r/min阶跃至500 r/min。图3（a）为定子磁链响应波形，（b）为a相定子电流响应波形，（c）为电磁转矩响应波形，（d）为电机转速响应波形。

从图4可以看出，在负载转矩不变，转速阶跃的状态下，改进后的DTC系统定子磁链轨迹接近圆形，没有较大波动，定子磁链幅值在电机运行过程中基本能够保持恒定，电机转速的动态响应很快，当t=1.0 s时，转速能够快速从原来的1 000 r/min达到50 r/min的给定值，且同时转矩动态响应较迅速，基本控制性能良好。图5为定子磁链在系统改进前后的轨迹。可以看出，传统的DTC系统定子磁链虽然大致为圆形，但磁链轨迹不是很光滑，存在一定程度上的磁链波动，而改进后系统的定子磁链轨迹比较圆滑，且磁链的抖动相对较小。

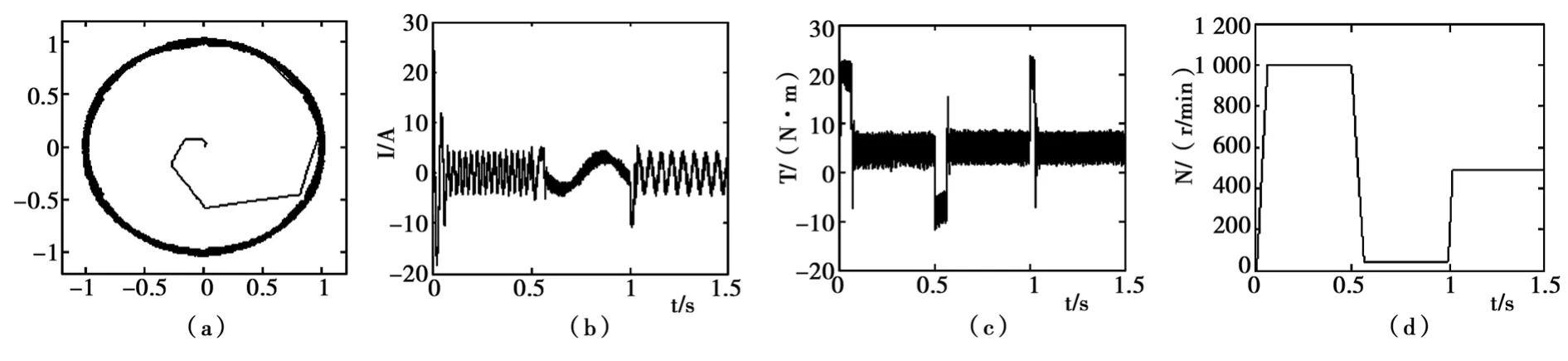
图3 实验波形图

图4 定子磁链波形图

3 结论

直接转矩控制技术的优点是显而易见的，但目前该技术在理论上尚不够成熟和完善。主要问题是:控制采用定子磁链定向，稳态机械特性与转子磁链定向相比差一些;低速性能不尽如人意。有待各个专家学者深入研究。

图5 定子磁链改进后波形图

［1］陈伯时.电力拖动自动控制系统——运动控制系统［M］.北京:机械工业出版社，2006:20-35.

［2］Depenbrock M.Direct Self-control（DSC）of Inverter-fed Induction Machine［J］.IEEE Trans.on Power Electronics，1988，3（4）:420-429.

［3］韩海涛.无速度传感器异步电动机直接转矩控制低速性能的改善［D］.大连交通大学硕士学位论文，2004:30-42.

［4］张宇林，蒋鼎国，焦竹青.异步电动机低速转矩脉动直接转矩控制研究［J］.电气传动，2008，38（9）:31-33.

［5］袁长江.基于SVPWM的异步电动机直接转矩控制系统的研究［D］.武汉理工大学硕士学位论文，2009:50-74.