基于小波变换的图像置乱加密算法研究

李 媛，张 培

（中北大学信息与通信工程学院，山西太原 030051）

0 引言

因特网技术的迅猛发展，多媒体通信成为人们信息交流的重要手段。数字图像、数字视频比传统的文字包含更多更广的信息量，因此，信息的保密与安全格外重要。置乱变换做进一步隐藏的预处理，可作为信息加密的一种方法。近年来，置乱算法有效应用于数字图像的预处理和后处理中，很大程度上保证了数字图像的信息安全，受到了众多学者的关注［1-3］。科研人员在这方面进行了探索并取得了很多的学术成果。如Amold变换、standard映射、Logistic映射等。本文通过小波、混沌和置乱等相结合的方法来研究数字图像的加密工作。

1 传统置乱加密算法

传统的图像置乱加密算法有两种，基于Amold变换的图像置乱加密算法和基于Logistic映射的图像置乱加密算法。

1.1 Logistic映射置乱加密原理［4］

Logistic映射是一个简单却又具有重要意义的非线性迭代方程，是由生物学家R.May于1976年提出的。方程的形式不包含任何随机因素，是完全确定的，但是由于具有非线性的特点，使它能够产生一系列的看似完全随机的，且极为敏感地依赖于分支参数μ的动态变化现象［5］。其定义由下式表示:

当分支参数μ=4时为满射，即Logistic-Map映射:

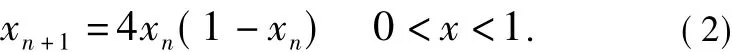
Logistic映射的输入和输出都分布在（0，l）上，Logistic映射序列的概率分布密度函数ρ（x）如下式所示:

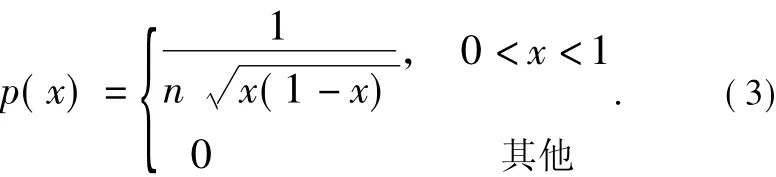
通过ρ（x），可以很容易地计算得到Logistic映射所产生的混沌序列中一些很有意义的统计特征。Logistic序列的以上特征表明，尽管混沌动力系统具有确定性，其遍历统计特性等同于白噪声。

1.2 基于Logistic映射的图像置乱加密效果与分析

对lena图像（尺寸为256×256）进行加密，加密结果如图1所示。其中初始值x0=0.1，参数μ=4，加密次数n=4。

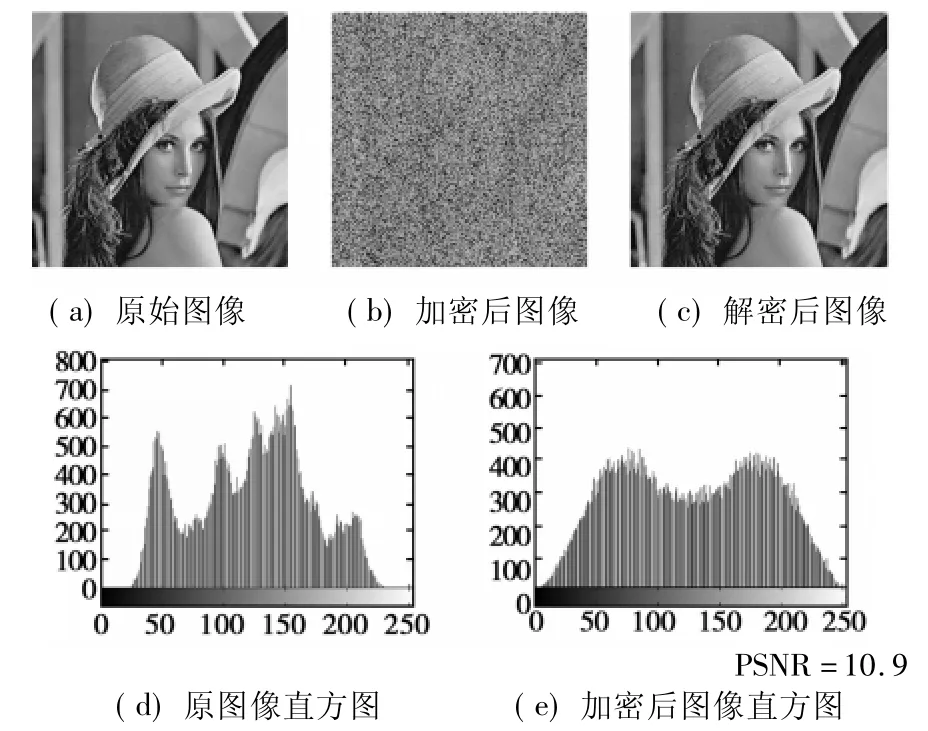
图1 基于Logistic映射的置乱加密效果

从视觉效果来说，加密图像混乱不可分辨，解密图像与原始图像几乎没有差别。根据Logistic混沌系统的敏感性测试结果可知，必须正确输入所有密钥才能正确解密图像。但是也存在一个问题，由图1可以看出加密图像的直方图虽然相对于原始图像平滑了一些，但是仍然存在明显的峰值，虽然加密图像混乱不可分辨，但是加密图像的直方图不平均，也就是说原始图像的像素灰度值的分布信息没有得到很好的保护，不能有效地抵抗图像的统计分析攻击。因此有必要研究加密效果更好，安全性更高的加密算法。

2 基于小波变换的图像置乱加密算法

在传统算法的基础上，本文实现了一种新的图像置乱加密算法，即基于小波变换的图像置乱加密算法。

2.1 基于小波变换的图像置乱方法

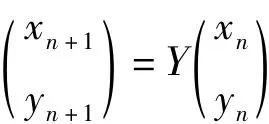
输入系统参数μ和初始值x0，采用混沌变换，迭代K+L次得到混沌序列xi，i=0，1…，K+L-1，为保证混沌系统的初值敏感性和参数敏感性（尤其在取整情况下），舍弃混沌系统的前L次迭代数据。因此，剩余混沌序列可用xi，j=0，1…，K+L-1表示。那么置乱矩阵T中（x，y）处元素t（x，y）的值可用（4）式得到:

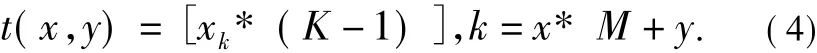
2.2 具体算法设计

根据混沌的参数敏感性、初值敏感性特点，本文设计的算法步骤如图2所示。

图2 基于小波变换的混沌图像置乱加密原理框图

（1）对原始图像进行二维离散小波变换，小波变换分解后的图像由四个子图像组成。

（2）对小波变换后的四个子图像的系数采用混沌变换置乱处理，混沌置乱后的图像也是由四个子图像组成。

（3）对混沌置乱后的图像进行小波逆变换即小波系数重构，得到加密后图像。

图像解密过程是加密的逆过程。首先根据密钥生成置乱序列和解密模版，对加密图像进行逆置乱，再恢复小波系数，然后根据小波系数重构图像，达到解密图像的目的。

2.3 基于小波变换的图像置乱加密效果与分析

用本算法对 lena图像（尺寸为256×256，灰度级 L=256）进行加密，实验结果如图3所示。预处理图像采用二维离散小波变换对图像进行小波分解，小波分解后的四个子图均采用相同的密钥进行混沌变换，混沌变换中的系统参数μ=3.925，初始值X0=0.1。

在小波变换域的图像加密算法中，由于混沌变换改变了小波系数的位置，使解密图像质量有所降低。通过峰值信噪比对解密图像和原始图像的一致性进行客观评价，得到解密图像与原始图像有较高的峰值信噪比PSNR=19.8230。加密后图像的直方图分布平均，加密后原始图像的像素灰度值的分布信息得到很好的保护，能有效地抵抗图像的统计分析攻击。

图3 基于小波变换的图像置乱加密效果

3 结术语

对基于Logistic映射的传统置乱加密算法和基于小波变换的图像置乱加密算法通过实验结果进行分析，Loglistic映射加密效果不错，但加密图像的直方图分布不平均，不能有效地抵抗图像的统计分析攻击。本文算法加密效果良好，直方图分布均匀，解密时必须正确输入所有密钥，非授权者用穷举法破密在有限的时间内是很难破密成功。分析表明此算法具有很高的安全性。

［1］孙秋艳.基于骑士巡游变换的图像置乱算法及评价方法［D］.南京航空航天大学硕士学位论文，2007:1-58.

［2］柏森.基于信息隐藏的隐蔽通信技术研究［D］.重庆大学自动化学院博士学位论文，2002:1-5.

［3］C.C.Chen，H.M.Shian，C.T.Shou.A New Encryption Algorithm for Image Crypto-systems［J］.Journal of Systems and Software，2001，58（2）:83-91.

［4］王改云，马姝靓.典型混沌系统的 Matlab仿真实现［J］.中国科技信息，2008，3:252-253.

［5］徐耀群，秦红磊.Logistic-Map混沌序列在二维置换网络中的应用［J］.哈尔滨工程大学学报，2002，23（3）:49-53.