基于土拱理论的土体坍塌机理研究

刘丹珠，张家发，李少龙，王丙杰

基于土拱理论的土体坍塌机理研究

刘丹珠，张家发，李少龙，王丙杰

（长江科学院水利部岩土力学与工程重点实验室，武汉 430010）

在均质堤基或典型双层堤基中由于各种原因形成土洞，其轮廓线是拱形。将土拱近似为三铰拱，应用结构力学中三铰拱合理拱轴线的求解方法，推导了土拱的近似合理拱轴线方程。应用太沙基提出的土拱效应存在条件，推导了在粘性土和无粘性土的土拱的最小拱高和最小拱厚计算公式，分析了拱形参数的合理性及形成稳定土拱的条件。应用本文的土体坍塌机理研究可以用来判断土洞的稳定性。

土拱效应；三铰拱；坍塌；最小拱高；最小拱厚

1 概 述

土拱效应［1］是屈服介质的应力向临近的非屈服介质的传递作用，这种传递作用是通过松散介质的抗剪强度来实现的，所以只有当松散介质的一部分有相对位移或有相对位移的趋势时，土拱效应才可能产生。

1884年，英国科学家罗伯茨首次观察到：粮仓底面所承受的力在粮食堆积高度约大于2倍底面直径后达到饱和而不再增加，并对此作了报道，丢失的质量到哪去了［2］？1895年，德国工程师詹森（H A JANSSEM）用连续介质模型对此现象做出了定量的解释，他在力学平衡方程中，加入由纵向压力产生的横向侧壁压力系数来考虑颗粒与仓壁之间的摩擦力，给出了粮食堆积高度与粮仓底面所承受的力的关系［2］。

1943年Terzaghi通过著名的活动门试验证实了土拱效应的存在，在对土拱的应力分布进行描述的基础上，得出土拱效应存在必需具备3个条件：①土体之间产生不均匀位移或相对位移；②作为支撑的拱脚的存在；③拱体形成处土体剪应力小于其抗剪强度［3］。

1980年，A N SCHOFIELD在进行河堤稳定研究时，提到过拱效应的产生。他认为，当承力层有一定厚度时，楔紧块将产生“拱作用”，阻止河堤的进一步垮塌［4］。

2003年，冯君等［5］将广泛用于隧道工程的普氏系数引入抗滑桩最大间距计算分析中，并根据桩间土拱的静力平衡确定了抗滑桩的最大间距。

2006年，赵明华等［6］考虑土拱效应分析了抗滑桩的合理间距分布，得到一个半经验的公式。上述应用土拱理论计算抗滑桩最大间距的计算方法得到了工程实例的验证，但其拱脚形式是结构物，拱体以上土体的压力全部传递到稳定结构物上。

朱碧堂等［7］曾对土拱效应做过详细的分析，认为在水平方向无限延伸的均质地层中形成的土拱如同一条拱形梁将作用在拱上的压力传递到拱脚和周围土体中，该法称为“拱形梁法”。贾海利等［3］应用“拱形梁法”把土拱假想为结构力学中的三铰拱，推导了基坑开挖形成的水平土拱的合理拱轴线方程，并依据土体拱脚处抗滑稳定性和土体拱脚处最危险截面满足库伦强度准则，确定了水平土拱的合理拱形参数。

2 均质地层土拱效应

2．1 拱轴线和支座反力的推导

土体自发形成土拱，拱形一定是最合理的，即三铰拱的拱轴线一定是合理拱轴线，拱体处弯矩M＝0。设上覆土体重度为γ（kN／m3），有效内摩擦角为φ（°），把物理模型概化为力学模型，如图1所示。拱顶到地层顶面的距离定义为上覆层厚度H（m），拱高用h（m）表示，拱跨用l（m）表示。拱所受的竖向分布荷载q＝γH＋γy，图中qc＝γH。在竖直荷载作用下，三铰拱的弯矩M由竖向荷载作用下简支梁的弯矩M0与FHy叠加而成。当拱体处都没有弯矩时（即上式两边对x求二阶导得

将q（x）＝qc＋γy代入（1）式得

当上覆土体自重一定时，水平支座反力FH为定值，解二阶微分方程得

图1 受上覆地层自重的三铰拱Fig．1 Three-hinged arch by overlying weight

边界条件：

将边界条件代入（3）式并注意到qc＝γH，得

式中：H为上覆土体厚度；FH水平支座反力。

三铰拱竖直方向的平衡方程和相同受力条件下相同跨度简支梁竖直方向的平衡方程相同。列竖直方向平衡方程，右侧拱受力分析如图2所示。

图2 右侧拱受力分析Fig．2 Forces of the right arch

化简（6）式得

铰点C处弯矩Mc＝0，对铰点C取力矩列平衡方程，得

将（5）式和（7）式代入（8）式化简得

可见，（9）式是一个关于未知数m的方程。

指数函数f（x）＝ez展开成z的幂级数

对于任意的z，ξ（ξ在0与z之间），余项的绝对值

e｜z｜有限的一般项，所以当n→∞时，有｜Rn（z）｜→0，即它的收敛半径R＝＋∞。

如果在z＝0处附近，用级数的部分和来近似代替ez，那么随着末项的增加，它们就越来越接近于e z。

双曲函数

反双曲函数

由以上推导可以得出双曲函数和反双曲函数在展开成幂级数时的收敛半径R＝∞。

将指数函数ez和e－z展开成泰勒级数，截取展开式的前五项用多项式的部分和代替ez和e－z，代回双曲函数sh z和反双曲函数ch z的表达式，得到双曲函数和反双曲函数近似表达式如下：

选取适当的拱高h、拱跨l和上覆层厚度H代回（19）式计算出m值，代回（9）式计算相对误差限，表达式为

图3 -h关系曲线Fig．3 Curve ofversus h

图4 -h／H关系曲线Fig．4 Curve ofversus h／H

从图3中可以看出：①当上覆层厚度H、拱跨l一定时随着拱高h的增大，相对误差限ε*r在逐渐增大。②当上覆层厚度H一定时，拱跨l在一定范围内变化对ε*r-h关系曲线无显著影响。

从图4中可以看出，ε*r随着h／H比值的增大而增大；h／H≤5，此时ε*r≤1．15×10－1。

2．2 最小拱高

形成稳定土拱后，对应一定拱跨和上覆层厚度，拱高的最小值称为最小拱高。最小拱高对应的拱圈以下土体在没有支护时将全部自动塌落。

太沙基对土拱效应做过详细研究，提出土拱效应存在时，拱体形成处土体剪应力应小于其抗剪强度。

拱脚处水平方向满足下式

式中：φ为土体的有效内摩擦角（°）；C为土体的粘聚力（kPa）；l为拱跨长度（m）。

将（21）式和（22）式代入（24）式取极限状态得

对于无粘性土，取土体的粘聚力C＝0。

将（24）式取极限状态得

将（21）式和（22）式代入（26）式得

式中：l为拱跨，h为拱高，均为大于或等于零的值，单位（m）；γ为拱脚区域土体重度（kN／m3）；φ为有效内摩擦角（°）；H为上覆土体厚度，单位（m）。

化简（27）式得

（28）式是关于未知数h的二次方程，解方程可以得到最小拱高hmin关于l，H，φ的表达式（当hmin／H比值较大时，公式需谨慎使用）。

当l＝0时，hmin＝0，取（29）式中的最小拱高。以下研究（29）式中最小拱高hmin随其它参数变化的关系。

因变量hmin相对于自变量l来说是增函数，当l＝0时，hmin＝0。且l≥0，所以hmin≥0。土体有效内摩擦角φ一定时，hmin-l关系曲线见图5。

对于无粘性土，从图5中可以得到以下结论：

（1）当φ一定时，随着l的增大，hmin逐渐增大；

（2）上覆层厚H越小，一定有效内摩擦角φ和拱跨l对应的最小拱高hmin越大；

（3）对比图5中的（a）和（b）图得：当上覆层厚H相等时，土体有效内摩擦角φ小的，一定拱跨l对应的最小，拱高hmin大。

图5 无粘性土中不同上覆层土体厚度H和有效内摩擦角φ时hmin-l关系曲线Fig．5 Relations of hminand l at different thickness of overlying soil and internal friction angleφin cohesiveless soil

当H趋近于无限大时，（30）式右端第二项分母中的二次项远大于一次项，hmin对H的偏导数趋近于零，所以当H趋近于无限大时，hmin趋近于定值。

从图6可以看出，当H＝0时，hmin≠0；但当上覆层厚度为零时，不能形成土拱效应，所以此点为奇点，应去除。

图6 无粘性土中不同拱跨l和有效内摩擦角φ时hmin-H关系曲线Fig．6 Relations of hminand H at different arch spans and internal friction angleφin cohesiveless soil

对于无粘性土，由图6可以得到以下结论：

（1）hmin-H关系曲线是减函数；

（2）对应一定拱跨l和有效内摩擦角φ，上覆层厚度H较小时，上覆层厚度H对最小拱高hmin的影响较大，且拱跨l越大，上覆层厚度H对最小拱高hmin的影响越大；

（3）由图6中的（a）和（b）图比较分析得到，对应一定拱跨l和上覆层厚度H，有效内摩擦角φ较小者最小拱高较大。

粘性土中由于粘聚力C的影响，最小拱高hmin随拱体跨度l、上覆土体厚度H的变化呈现与无粘性土不一样的规律。

令

确定土体在水平方向满足稳定性时的最小拱高hmin，化简（25）式得

（33）式中比（28）式多了k的影响项。

令

由于跨度l＝0时，拱高hmin＝0，所以hmin＝（33）式比（28）式多了综合参数k的影响项，由于k的影响项中无拱体跨度l，所以相对自变量拱体跨度l也是增函数，即l≥0时，hmin≥0。将拱体跨度l、上覆土体厚度H、土体参数γ，C，φ代入（34）式可以得到最小拱高hmin的数值。以下通过曲线图图7和图8来描述（33）式的性质。

对于粘性土，由图7中可以得到以下结论：

（1）当土体参数一定时，不同的上覆层厚度H，粘性土中最小拱高hmin随l变化的关系曲线都几乎呈直线；

（2）上覆层厚度H对最小拱高hmin的影响比无粘性土大；

（3）对比图7的（a）和（b），当上覆层厚度H和拱跨l一定时，土体参数γ，C，φ小的对应的最小拱高大。

图7 粘性土一定上覆层厚度和有效内摩擦角φ时hmin-l关系曲线Fig．7 Relations of hminand l at different thickness of overlying soil and internal friction angleφin clay

图8 粘性土一定拱跨l和有效内摩擦角φ时hmin-H关系曲线Fig．8 Relations of hminand H at different arch spans and internal friction angleφin clay

从（33）式中分析得到，当H＝0，l＝0时，hmin≠0，但当上覆层厚度为零，且拱跨也为零时，不能形成土拱效应，所以此点为奇点，应去除。

对于粘性土，由图8可以得到以下结论：

（1）hmin-H关系曲线是增函数；

（2）对应一定拱跨l的相同土性的土体，随着上覆层厚度H的增大，hmin-H关系曲线趋于平缓，最小拱高hmin将趋于一个稳定的值；

（3）对比图8中的（a）和（b），对应一定拱跨l和上覆层厚度H，强度较高者最小拱高较小。

2．3 最小拱厚

对应一定拱跨、拱高、上覆层厚度，拱圈厚度的最小值称为最小拱厚（等价于拱体厚度）。当上覆层厚度小于最小拱厚时，不能形成土拱，上覆土体将全部坍塌。

均质地层中形成的土拱，土体拱脚处最危险截面应满足摩尔－库伦强度准则，依据右侧拱脚B最危险截面处土体的极限平衡条件，应力分析如图9所示，建立拱厚t和其他变量的关系，计算出要形成土拱时的最小拱厚。取轴力与竖直方向的夹角为φ，根据几何关系可得φ＝φ。无粘性土粘聚力C＝0，粘性土粘聚力C＞0。

图9 右侧拱脚B应力分析Fig．9 Stress analysis for the right arch foot B

式中：σ1，σ3分别为最大和最小主应力；C为土体粘聚力；φ为有效内摩擦角。

式中：σ1f，σ3f分别为最大和最小极限主应力；t为拱体厚度。

将（37）式和（36）式代入（35）式求得在均质粘性土中一定拱高和拱跨对应的最小拱厚

对于无粘性土，C＝0。

最小拱厚tmin和土体强度参数，拱跨l，上覆层厚度H和拱高h有关。

3 典型双层堤基土拱效应

上层为粘性土，下层为无粘性土的双层堤基，设粘性土层厚度为H1，粘性土土体重度为γ1，有效内摩擦角为φ1，粘聚力C1；无粘性土土体重度为γ2，有效内摩擦角为φ2。拱顶到两地层交界面距离为H2，当H2≥0时，拱顶在无粘性土中；当H2＜0时，拱顶在粘性土中。

3．1 拱顶在无粘性土时的土拱效应

当拱顶在两地层交界面以下时，H2≥0，此时拱圈所受的竖向分布荷载q＝γ1H1＋γ2H2＋γ2y，令γ1／γ2＝a，定义名义上覆层厚度H′＝（aH1＋H2），由于拱圈和拱脚都在无粘性土中，成拱原理与均质无粘性土中的成拱原理一样。只需将无粘性土重度γ2，名义上覆层H′，无粘性土的有效内摩擦角φ2代入（21）式，（22）式，（23）式，（25）式，（39）式就可以求取拱顶在两地层交界面以下时的土拱参数。三铰拱力学模型如图10所示。

图10 拱顶在地层交界面以下时的三铰拱Fig．10 The three-hinged arch of arch crest below the interface

右侧拱受力分析如图11所示，应力分析如图12所示。

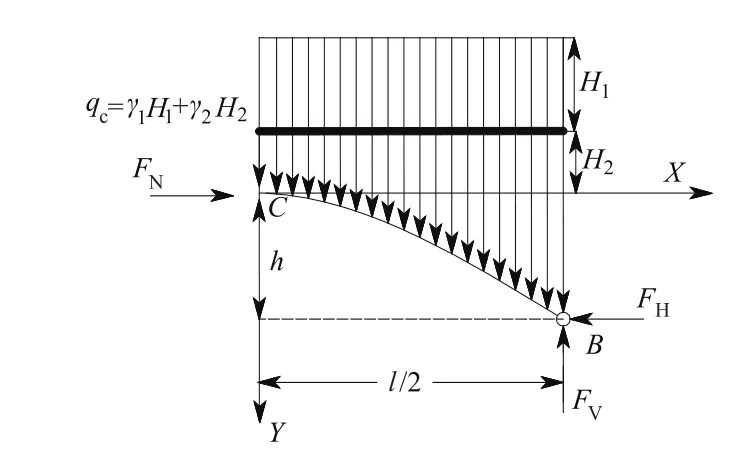
图11 右侧拱受力分析Fig．11 Force analysis for the right arch

3．2 拱顶在粘性土时的土拱效应

拱顶在两地层交界面以上时，粘性土中有部分拱圈，粘性土粘聚力对此部分拱圈有力学作用，H2＜0，近似概化粘性土粘聚力对粘性土中拱圈的影响。

假设土拱在均质粘性土中形成，上覆层厚度H＝H1＋H2，将上覆层厚度H，拱跨l代入（33）式，求取最小拱高hmin，用H′2＝h－hmin1－H2计算H′2。

图12 右侧拱应力分析Fig．12 Stress analysis for the right arch

如果H′2≥0，则拱顶在无粘性土，返回到3．1小节中求取对应土拱参数。

如果H′2＜0，拱顶在粘性土中，则粘性土区域中的合理拱轴线和最小拱厚是土拱在均质粘性土中形成求取的合理拱轴线和最小拱厚，无粘性土区域中的合理拱轴线是土拱在均质无粘性土中形成求取的合理拱轴线。三铰拱力学模型如图13所示。

图13 拱顶在地层交界面以上时的三铰拱Fig．13 The three-hinged arch of arch crest above the interface

4 结 语

本文研究取得以下结论：

（1）用“拱形梁法”推导了受上覆土体自重的土拱的合理拱轴线，通过化简得到三铰拱水平和竖向支座反力。计算求取了土拱合理拱轴线的显式近似解析解，对近似解开展了误差分析。

（2）用太沙基提出的土拱存在条件推导了2种土性（粘性土和无粘性土）土拱的最小拱高和最小拱厚公式。

（3）分析了无粘性土和粘性土中形成稳定土拱的条件。

（4）用本文基于土拱理论的土体坍塌机理可以判断均质土体中各种原因形成的土洞的稳定性。

（5）本文用理想条件下均质散粒体的物理力学参数（γ，C，φ），推导了无粘性土和粘性土中形成稳定土拱所需的最小拱高和最小拱厚公式，解释了土拱形成的机理。

（6）以上推导和分析已经做了一些算例的验证，但还需要进一步补充和完善。

致谢：在写论文期间，文松霖教授、饶锡保教授和潘家军博士给予了指导和帮助，在这里表示深深的谢意！

［1］ RICHARD LH．The Arch in Soil Arching［J］．Journal of Geotechnical Engineering，1985，111（3）：302－31．

［2］ 厚美英，陆坤权．奇异的颗粒物质［J］．产业论坛，2001，2（2）：26－28．（HOU Mei-ying，LU Kun-quan．Fanciful Particulate Matter［J］．Industry Forum，2001，2（2）：26－28．（in Chinese））

［3］ 贾海莉，王成华，李江洪．关于土拱效应的几个问题［J］．西南交通大学学报，2003，38（4）：398－402．（JIA Hai-li，WANG Cheng-hua，LIJiang-hong．Discussion on Some Issues in Theory of Soil Arch［J］．Journal of South-west Jiaotong University，2003，38（4）：398－402．（in Chinese））

［4］ SCHOFIELD A N．Cambridge Centrifuge Operation［J］．Geotechnique，1980，3（30）：227－268．

［5］ 冯 君，吕和林，王成华．普氏理论在确定抗滑桩间距中的应用［J］．中国铁道科学，2004，24（6）：79－81．（FENG Jun，LV He-lin，WANG Cheng-hua．Application ofM．M．PROMOJIYFAKONOV Theory to Solution of Dis-tance Between Anti-slide Piles［J］．Chinese Railway Sci-ence，2004，24（6）：79－81．（in Chinese））

［6］ 赵明华，陈炳初，刘建华．考虑土拱效应的抗滑桩合理桩间距分析［J］．中南公路工程，2006，31（2）：1－3．（ZHAO Ming-hua，CHEN Bing-chu，LIU Jian-hua．A-nalysis of the Spacing Between Anti-Slide Piles Consider-ing Soil Arch Effect［J］．Central South Highway Engineer-ing，2006，31（2）：1－3．（in Chinese））

［7］ 朱碧堂，温国炫，刘一亮．基坑开挖和支护中土层拱效应的理论分析［J］．建筑技术，2002，33（2）：97－98．（ZHU Bi-tang，WEN Guo-xuan，LIU Yi-liang．Theoreti-cal Analysis on Arching Effect of Soil in Excavation and RetainingWorks［J］．Architecture Technology，2002，33（2）：97－98．（in Chinese））

（编辑：罗玉兰）

Intelligentmodels including Grey Model（GM（1，1）），BP neural network，and the combination of the twomodels Grey Neural Network Model（GNNM（1，1））were employed in the prediction of anchorage foundation deformation．Monitored soil pressure of the north anchorage foundation of Runyang Bridge was taken to dynamically predict the deformation by these threemodels．The predictionswere further compared with themeasured soil pres-sures．The comparison showed that there is a relative error of 1．11%，0．77%and 0．43%respectively of each model’s prediction result．Compared with the other twomodels，the prediction of GNNM（1，1）was closer to the measured soil pressure，and it can be applied in actual prediction process as it ismore appropriate for curve fitting nonlinear data and large-fluctuation data．

Intelligent Prediction of Anchorage Foundation Soil Pressure for Large Span Suspension Bridge

REN Li-fang1，YUAN Bao-yuan2
（1．Department of Economics and Management，Shijiazhuang Institute of Railway Technology，Shijiazhuang 050041，China；2．School of Earth Science and Engineering，Hohai University，Nanjing 201198，China）

anchorage foundation，intelligentmodel，soil pressure prediction，gray BP neural network

TV16

A

1001－5485（2011）05－0035－07

2010-06-28

国家重点基础研究发展计划（2007CB714106）

刘丹珠（1984-），男，江西铜鼓人，硕士，主要从事渗流和地下水环境的研究工作，（电话）15271932007（电子信箱）ldzliudanzhu＠163．com。