基于模糊Bernardo理论的联合体投标不确定博弈合作决策
姚若军
(1.华能西藏发电有限公司,四川 成都 610017;2.四川大学水电学院,四川 成都 610065)
联合体工程投标需要各伙伴商充分信任与合作,发挥各自的核心优势,共享各种资源,分担风险与利润,因此确定伙伴商是联合体投标成功的关键。在进行伙伴商选择时,必须多方面权衡各种因素,全面考察潜在的伙伴商,从中做出最优化的选择。通过对潜在伙伴商的特征信息进行分析、整理、评估,确定一个最优联合体构成方案十分重要。
博弈收益的超可加性是形成工程投标联合体的必要条件[1]。在所有满足超可加性条件的联合体中,分析和评价联合体的优劣序应考虑决策者博弈优选的偏好,具有模糊特性,且属于不确定性群决策范畴。基于模糊事件的可信性测度概念[2],利用可能性理论推广Bernardo方法[3],给出一种更客观合理的模糊群决策方法,并将该方法应用于利益相关博弈者的优势合作联合体伙伴商的选择中。在模糊资源约束的合作博弈环境下,给出联合体博弈合作的模糊机会约束混合整数规划模型及求解方法,且在联合体目标不同时对模型作自适应调整,达到博弈合作的最优态势。
1 基于模糊Bernardo理论的联合体伙伴商选择模型
Bernardo群决策方法的主要思路是寻找描述各成员对备选对象的优劣看法的一致性程度的指标,并使该指标极大化,然后将备选对象的优劣排序问题转化为求解混合0-1规划问题[4]。根据博弈环境复杂性及博弈者思维模糊性的特点,考虑博弈群体的权重和位次效用,根据模糊Bernardo方法对所有可能结成的博弈联合体进行优先排序。
设A={A1,A2,…,An}为投标联合体,p个伙伴商联合投标决策群体D={D1,D2,…,Dp}为A的子集。Dk(k=1,2…,p)为第k个伙伴商,要在含m个评价指标的集合C={C1,C2,…,Cm}中选定一定数量的指标对A进行评价。记Vague值 vi=
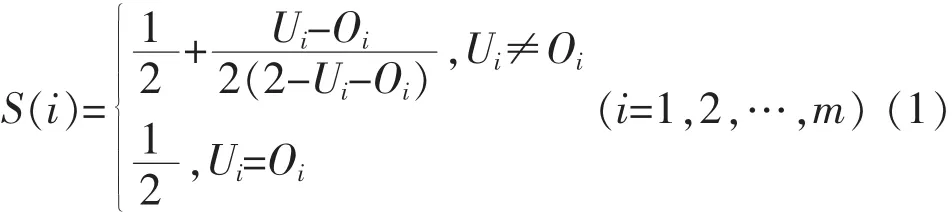
按公式(1)选出评价指标建立评价指标体系C={C1,C2,…,Cm}。
在联合体伙伴商选择的不确定环境下,假设评价指标体系C={C1,C2,…,Cm}的模糊权重向量为其中模糊数(i=1, 2…,m)为第i指标的模糊权重,m'为评价指标个数,将向量归一化得再设是博弈者(伙伴商)Dk(k=1, 2, …,p)的模糊决策权重,则D的模糊决策权重向量为=归一化得
若用指标 i评价 Dk将 Aj排在第 t(t=1,2,…,n)位,则令变量;否则,令。因为各指标及各博弈决策者有差异,故引入模糊变量表示D在Aj排在t第位的集结模糊权重,有

运用Zadeh扩展原理可以进行模糊数运算,将D对各博弈者的评价进行集结得到集结矩阵:

评价投标联合体优劣序的核心问题是寻找入选伙伴商的内涵进行描述的一致性指标,并使其达到极大值。这首先需要计算累积模糊协商矩阵,其中表示博弈者 Aj被排在前t位的总集结模糊权重。若Aj排序越靠前,则它的合作效用越大。设博弈者集合A位次效用向量 Q(q1,q2,…,qn),其中 qt=n/t,(t=1,2,…,n)。利用位次效用修正矩阵R,得到R'=r'jt,其中r'jt=qtrjt。根据矩阵R'对所有可能结成的联合体进行优劣总排序。若D把某个联合体中的Aj排在第t位,则令yjt=1,否则令yjt=0,构造模糊协商函数f为:

式中 h∈{1,2,…,n}表示入选伙伴商的数量,p 是D的人员数。可见,协商函数是描述群体对联合体成员数目为时的一致性指标。
投标联合体组建的资源约束使得所有伙伴商不一定都能入选到某个特定的联合体中,故集合A变为且对任意k≤z,应满足考虑资源的约束,可令模糊数bjg是Aj的第g个约束因素的模糊值,实数vg是第g资源的总量,有

式中Ω为资源约束种类数。
投标联合体伙伴商选择的模糊约束混合0-1规划模型[6]为:

由式(5)即可求解出投标联合体伙伴商数目为h时的最优联合体,即max maxf=所对应的联合体就是在不考虑伙伴商数量限制时的最优联合体。
2 模型求解


则可信性测度Cr:

由刘宝碇提出的随机模糊机会约束规划理论[7],可将模型(5)转化为标准模糊机会约束规划模型:
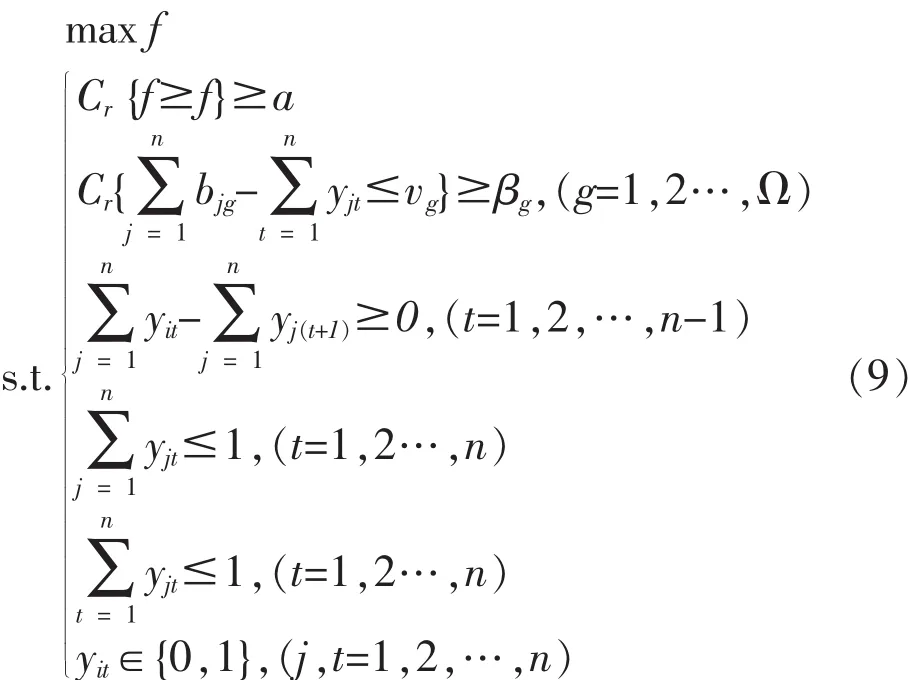
式中a,βg是决策群体预先给定的置信水平;f是不超过f的实数值。
在实际投标联合决策中,决策群体通常会考虑模糊资源约束和f的优先序。在给定置信水平βg时,第g资源不超过总量限制vg∈R,则
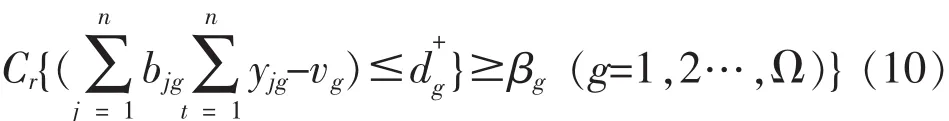

式中d-∈R是模糊目标的负偏差,其优先序位居第二。可见,模型(9)可转化为标准模糊机会约束的0-1目标规划模型:

表2 施工企业可利用资源与可用投标资源

表3 依据指标排序结果

式中符号同前。
3 应用
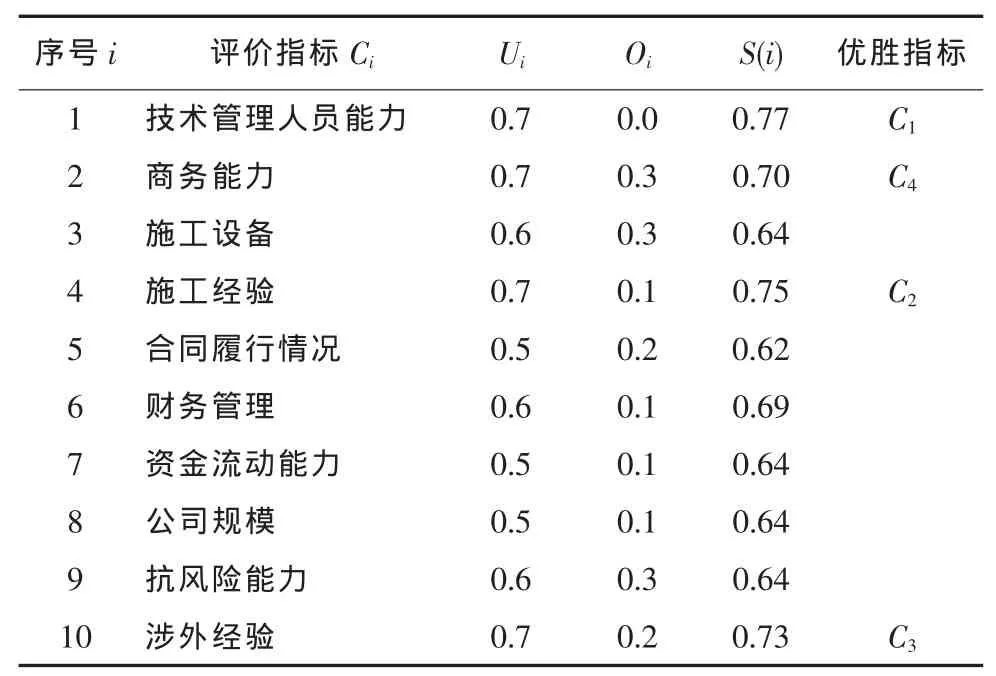
表1 评价指标及评选结果
某水电施工企业参与国际投标,为增强其综合投标能力,拟定3家国内施工企业A={A2,A3,A4}与其组成联合体投标。
第一步,选定决策群体 D={D1,D2,…,D5},采用 L-R 型模糊数(a,τ,δ)表示模糊信息,其模糊决策权重为=[(0.7,0.1,0.1),(0.8,0.1,0.1),(0.9,0.1,0.1),(0.7,0.1,0.1),(0.8,0.1,0.1)];
第二步,选择施工企业能力评价指标,见表1。
根据指标重要性选择结果,选定4个评价指标 C1,C2,…,C4,且权重为 w=[(0.7,0.2,0.1),(0.7,0.1,0.1),(0.9,0.1,0.1),(0.8,0.1,0.2)]
4家施工企业可以利用的资源和所需资源见表2。
第三步,从其余3家施工企业中寻找几家施工企业,以实现在资源约束下入选指标C1~C4最大化。
归一化决策权重和评价指标权重得:
λ=[(0.18,0.05,0.05),(0.21,0.05,0.05),
(0.23,0.06,0.06),(0.18,0.05,0.05),
(0.21,0.05,0.05)]
W=[(0.18,0.05,0.05),(0.21,0.05,0.05),
(0.23,0.06,0.06),(0.18,0.05,0.05),
(0.21,0.05,0.05)]
根据指标C1~C4对各施工企业进行排序,分析结果见表3。所有可能的联合体集合为{A1,A2},{A1,A3},{A1,A4},{A1,A2,A3},{A1,A2,A4},得模糊协商矩阵:

修正累计模糊协商矩阵:

设 f'=0.20,置信水平 a=0.95,βg=0.80(g=1,2,3,4),则得计算结果见表4。
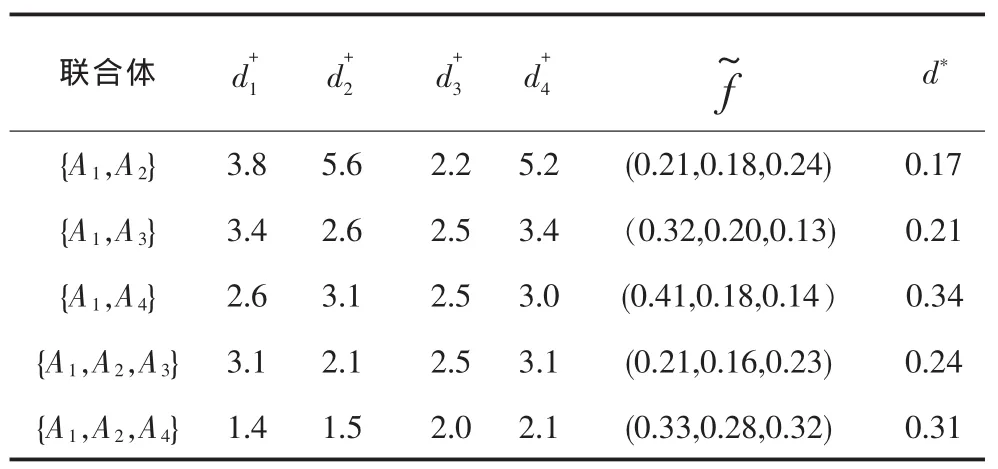
表4 联合体及其偏差分析
由表 4可见博弈组合{A1,A2,A4}约束偏差最小,该施工单位应与施工企业A2、A4组成联合体参与投标。
4 结语
联合体投标环境的不确定性和决策者经验的模糊性导致联合博弈的优先序关系的不确定性。基于模糊Bernardo的群决策集成不确定理论和模糊理论,使模糊协商函数、模糊约束偏差极小化,将联合体博弈优选问题转化为模糊机会约束的规划问题。针对联合体目标不同,有相应的博弈规划模型,这种联合体博弈合作决策具有较强的自适应性。

[1]Owen G.Game theory[M].New York:Academic Press,1982:143—165.
[2] Liu B.Chance constrained programming with fuzzy parameters[J].Fuzzy Sets and Systems,1998,94 (1) :227—237.
[3] Bernardo J J.An assignment approach to choosing R&D experi ment s[J].Decision Science,1977,8(2):489—501.
[4] Carlsson C,Fuller R.Fuzzy reasoning in and optimization[M].Heidelberg,Germany:Physica -Verlag,2002:123—148.
[5]Hong D H,Kim CA A Note on Similarity Measure between Vague Sets and between Elements[J].Inf.Sci,1999,135(1):83—96.
[6]Liu Y K,Liu B.Random fuzzy programming with chanc measures defined by fuzzy integrals[J].Mathematical and Computer Modeling,2002,36(4—5):509—524.
[7] 刘宝碇,赵瑞清,王纲.不确定规划及应用[M].北京:清华大学出版社,2003:178—182.

