微型滚珠丝杠副摩擦力矩模型的建立与实验验证
陈勇将 汤文成
(东南大学机械工程学院,南京 210096)
微型滚珠丝杠副的摩擦力矩是指各种摩擦因素对微型滚珠丝杠副运动构成的阻力矩,其带来的能量损耗降低了传动效率,引起的温升产生热变形影响了定位精度[1-2].对于广泛应用于高精度小型机电一体化设备的微型滚珠丝杠副来说[3],摩擦力矩模型的建立十分必要,可以快速且准确地预测能量损耗与温升速率.
文献[4]建立了一个估计滚珠丝杠副摩擦力矩的模型,主要参考了滚动轴承建立摩擦力矩模型的方法,没有考虑自旋滑动摩擦及滚珠丝杠副独有的螺旋结构对摩擦力矩的影响,且没有进行实验验证.文献[5]将文献[4]建立的滚珠丝杠副摩擦力矩模型计算结果与文献[6]测量到的滚珠丝杠副摩擦特性数据进行了比较,发现文献[4]建立的摩擦力矩模型计算结果与实验数据存在较大差异.
本文从微型滚珠丝杠副的摩擦机理出发,得出影响摩擦力矩的各种阻力与阻力矩;考虑自旋滑动摩擦及螺旋升角的影响,推导出适用于微型滚珠丝杠副的摩擦力矩模型;通过实验对模型进行验证.
1 微型滚珠丝杠副的摩擦机理
微型滚珠丝杠副中接触面虽为滚动界面,但滚动接触所引起的摩擦损耗很少,损耗主要来自于滚动过程中发生的滑动行为.这些滑动产生于滚珠与丝杠滚道接触界面间、滚珠与螺母滚道接触界面间、滚珠与返向器滚道接触界面间和滚珠与滚珠接触界面间(见图1),其中滚珠与丝杠滚道、滚珠与螺母滚道及滚珠与返向器滚道接触界面间的滑动摩擦为损耗的主要来源.返向器是螺母的一部分,所以滚珠与返向器滚道接触可看作滚珠与螺母滚道接触的特例,将这3个接触界面间的滑动摩擦统称为滚珠与滚道接触界面间的滑动摩擦.
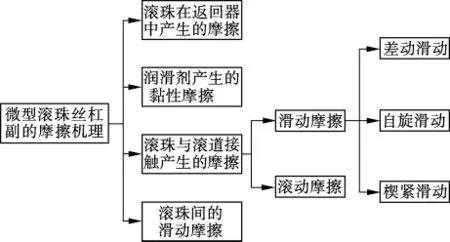
图1 微型滚珠丝杠副的摩擦机理分解图
1.1 滚珠与滚道接触产生的摩擦
微型滚珠丝杠副中滚珠与滚道间的纯滚动与滑动一样也会发生能量损耗,主要是接触表面的应力循环引起的黏着损失和弹性滞后损耗.虽然滚动接触发生在离散的微凸体上,但由于滚动表面的微凸体沿着法向接近和分离,不像滑动接触那样沿着切线方向,因而滚动接触面积变化不大;滚动接触区的黏着力主要来自范德华力,黏着力将在滚动接触区末端以拉伸形式被分离,而不像滑动接触那样以剪切形式产生分离,所以滚动接触所引起的摩擦损耗较滑动摩擦相比很少.滚动摩擦的弹性滞后损耗源于消耗功与复原功之差,单个接触点处由弹性滞后所形成的摩擦力矩为[7]
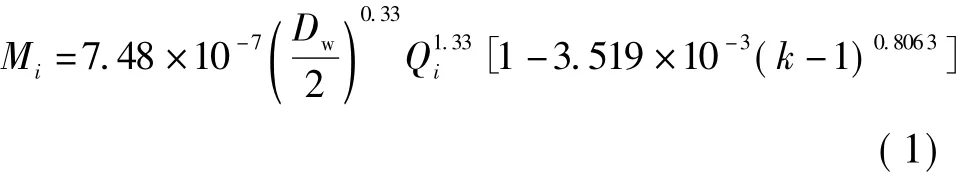
式中,Dw为滚珠直径;Qi为滚珠与滚道间的法向载荷;k为滚珠与滚道接触的椭圆率.
滑动摩擦主要包括楔紧滑动、差动滑动和自旋滑动.楔紧滑动源于滚珠丝杠副的螺旋结构,是滚珠丝杠副特有的运动,而滚珠与滚道间的接触变形引起的差动滑动,仅在2条窄带上不发生滑动,同时由于接触角的存在,滚珠丝杠副中还将引起绕纯滚动点的自旋滑动.当滚珠与滚道接触区域上存在2条纯滚动线时,差动滑动摩擦力矩MCi和自旋滑动摩擦力矩MPi的计算公式为[8]

式中,μ为滑动摩擦系数;l为接触椭圆的长半径;ri为滚珠与滚道间接触变形后的半径;fc,fp分别为差动滑动MCi和自旋滑动MPi计算系数.
1.2 滚珠在返向器中产生的摩擦
滚珠在返向器中的摩擦主要为滚珠进出返向器时碰撞力产生的摩擦和滚珠在返向器滚道内的滑动摩擦[9].由于滚珠在返向器中不承受载荷,所以滚珠中心的线速度不高,相对于滚珠与丝杠滚道及滚珠与螺母滚道产生的滑动摩擦而言,这一部分摩擦很小,通常情况下可以忽略.碰撞力产生的摩擦与丝杠转速成正比,高速下这一部分摩擦较大[10-11],但微型滚珠丝杠副的应用领域对转速要求不高,因此这一部分摩擦也不作考虑.
1.3 润滑剂产生的阻力及滚珠间的滑动摩擦
在流体润滑微型滚珠丝杠副中,滚珠必须克服润滑剂产生的黏性摩擦力.润滑剂产生的阻力取决于散布在滚珠丝杠副内部润滑剂的量.运用弹流润滑理论求得润滑剂引起的滚动阻力为[7]
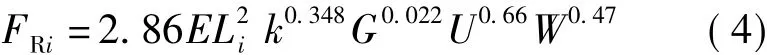
式中,E为等效弹性模量;Li为滚珠与滚道间接触点法向平面内的综合曲率半径;G为材料参数;U无纲量速度参数;W为载荷参数.
微型滚珠丝杠副的螺旋传动难以实现在滚珠间加上类似于轴承的保持架,所以滚珠间的滑动摩擦力无法避免,滚珠间摩擦产生的摩擦力矩可表示为
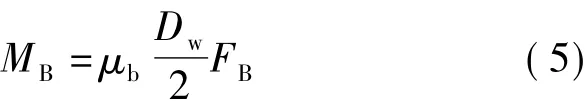
式中,μb为滚珠间摩擦系数;FB为滚珠间摩擦力.
2 摩擦力矩模型的建立
2.1 滚珠与滚道接触的摩擦力
微型滚珠丝杠副中滚珠与滚道接触的摩擦力FSi可以通过滚珠上力与力矩的平衡关系式求得.由微型滚珠丝杠副摩擦机理可知,作用于滚珠滚动方向的阻力除了滚珠与滚道间摩擦力FSi外,还有滚珠间接触力FB及润滑剂引起的滚动阻力FRi和压力FPi;而作用于滚珠上沿运动方向绕滚珠球心的阻力矩主要为差动滑动摩擦力矩MCi、弹性滞后阻力矩Mi及滚珠间摩擦力矩MB(见图2),由力和力矩平衡可得
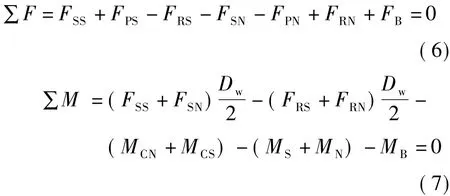
式中,FSS为滚珠与丝杠滚道间的摩擦力;FSN为滚珠与螺母滚道间的摩擦力;FPN为滚珠与螺母滚道间的润滑剂引起的压力;FPS为滚珠与丝杠滚道间的润滑剂引起的压力;MCN为滚珠与螺母滚道间的差动滑动摩擦力矩;MCS为滚珠与丝杠滚道间的差动滑动摩擦力矩;MN为滚珠与螺母滚道间的弹性滞后阻力矩;MS为滚珠与丝杠滚道间的弹性滞后阻力矩.

图2 单个滚珠所受力与力矩平衡关系图
由式(6)和(7)解得FSS和FSN的表达式为
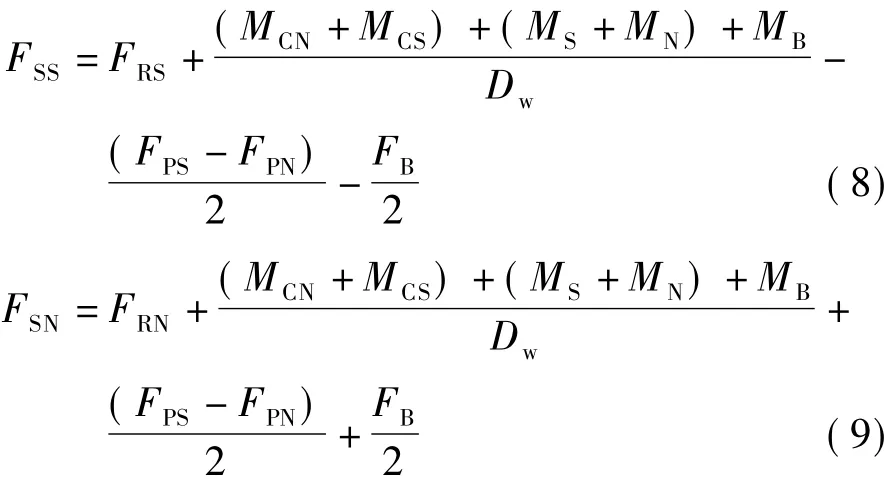
润滑剂作用于滚珠球心的压力FP可以表示成以FR为变量的函数,即
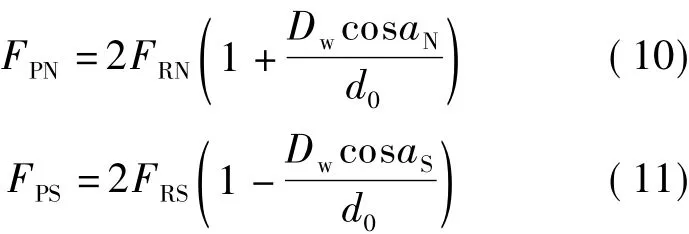
式中,d0为微型滚珠丝杠副的公称直径;aS为滚珠与丝杠滚道的接触角;aN为滚珠与螺母滚道的接触角.
将式(10)和(11)代入式(8)和(9)可得滚珠与滚道接触界面间摩擦力的最终表达式为
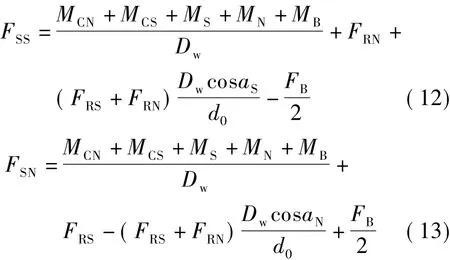
2.2 滚珠与滚道接触的摩擦力矩模型
对于微型滚珠丝杠副中单个滚珠的摩擦力矩,除了包含滚珠与滚道间摩擦力与力臂之积外,还应将自旋滑动摩擦力矩MPi投影至旋转轴上(见图2),其分量应为MPisinaicosβ,因此单个滚珠与滚道接触的摩擦力矩表达式为

式中,RS为滚珠与丝杠滚道接触点至丝杠轴心的距离;RN为滚珠与螺母滚道接触点至丝杠轴心的距离;β为螺旋升角.
因此,对于滚珠数为Z的微型滚珠丝杠副,其摩擦力矩最终表达式为
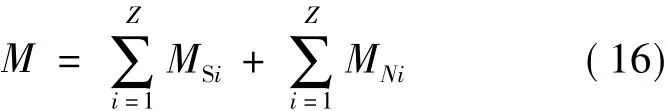
3 摩擦力矩模型的实验验证
3.1 试验设备及方法
微型滚珠丝杠副摩擦力矩的测量是在微型丝杠综合测试实验台上进行的,测量实验台结构如图3所示.由安装在工作台上的驱动电机与滚珠丝杠副的一端连接带动旋转,另一端用尾座顶尖限制,通过摩擦力矩测量装置的悬臂与安装在螺母上连接杆相配合,来约束滚珠丝杠副的周向与轴向运动.当丝杠旋转时,螺母旋转运动被限制只能带动摩擦力矩测量装置在滑动导轨上作轴向运动,在此方向上由气压缸施加轴向载荷给滚珠丝杠副,此轴向力的大小由拉压式力传感器测得.而限制周向运动的阻力由压力传感器测得,转换成数字信号后,乘以力臂因子即可得到所测量的微型滚珠丝杠副的摩擦力矩.

图3 微型滚珠丝杠副综合测试实验台结构示意图
试验产品为FF型微型滚珠丝杠副(南京工艺装备制造有限公司),具体结构参数及性能参数如表1所示.被测试的微型滚珠丝杠副首先以400 r/min的转速跑合5 min后停转,然后保持轴向载荷恒定,再调节驱动电机转速从零增加到800 r/min.在这期间测量螺母移动方向与轴向载荷方向相反时的摩擦力矩,为验证试验结果的准确性和可重复性,同一转速下重复测量多次.试验时测量参数的采集频率设置为100,力臂直径为38 mm.

表1 FF1605型微型滚珠丝杠副结构与性能参数
3.2 结果与讨论
图4所示为FF1605型微型滚珠丝杠副在不同转速下测得的摩擦力矩值及其变化范围,摩擦力矩是在同一转速下螺母移动方向与轴向载荷方向相反时重复试验多次所取的平均值.由图4可知,在较低转速(n=400 r/min)下,摩擦力矩的变化幅度较大,随着转速的增加,摩擦力矩的变化速度有所放缓;微型滚珠丝杠副的摩擦力矩极不平稳,存在较大的波动,且波动范围的大小与转速没有明显关联,这主要是由于影响微型滚珠丝杠副的因素较多,因而摩擦力矩特性具有随机性和复杂性.
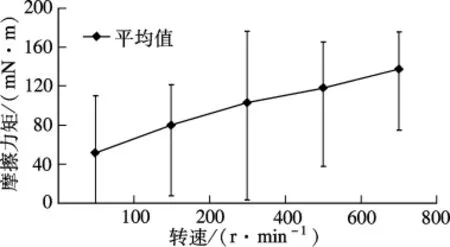
图4 不同转速下微型滚珠丝杠副的摩擦力矩实验值及变化范围
由不同转速下摩擦力矩实验值与模型值对比可知(见图5),不同转速下微型滚珠丝杠副的摩擦力矩模型值与实验值都有较好的吻合.随转速的提高,摩擦力矩模型值一直以较大的速度上升,而实验值在n=400 r/min以下与模型值上升速度相近,尤其当转速为400 r/min时两值误差几乎为零.但随着转速进一步升高,实验值的上升速度慢于模型值,但上升趋势不变.
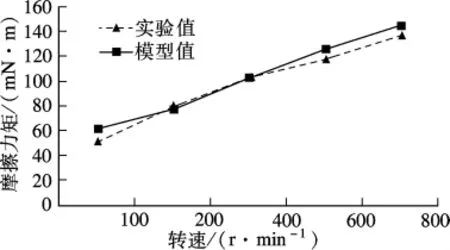
图5 不同转速下微型滚珠丝杠副的摩擦力矩模型值与实验值对比图
4 结论
在拟静力学分析基础上,考虑了微型滚珠丝杠副螺旋升角及自旋滑动摩擦的影响,利用力与力矩平衡的方法,推导出了微型珠丝杠副摩擦力矩模型,实验证明所建立的新摩擦力矩模型基本符合实际情况.由依据微型滚珠丝杠副摩擦机理建立的新模型可知,润滑介质的性能参数及滚珠与滚道接触的滑动摩擦系数对摩擦力矩影响较大,实验也表明摩擦力矩的变化主要是转速影响了滚珠所受的润滑剂黏性阻力,因此要减小微型珠丝杠副摩擦力矩、提高摩擦力矩的平稳性,需要特别重视润滑的研究.
References)
[1] Brecher C,Witt S,Yagmur T.Infuence of oil additives on the wear behavior of bal screws[J].Production Engineering,2009,3(3):323-327.
[2] Wei C W,Lin J F.Kinematic analysis of the ball screw mechanism considering variable contact angles and elastic deformations[J].Journal of Mechanical Design,2003,125(4):717-733.
[3]严虎勤,闫笃政,田茂林.HJ微型滚珠丝杠副的设计与制造[J].制造技术与机床,2006,4(9):109-110.Yan Huqin,Yan Duzheng,Tian Maolin.Design and manufacture of micro-type ball screw[J].Manufacturing Technology & Machine Tool,2006,4(9):109-110.(in Chinese)
[4] Olaru D,Puiu G C,Balan L C,et al.A new model to estimate friction torque in a ball screw system[C]//Advanced Computer Aided Design of Ecological Products.Brasov,Romania,2004:333-346.
[5]苏益德.滚珠导螺杠之摩擦力分析研究[D].中国台湾:中兴大学机械工程系,2009.
[6] Kamalzadeh A.Precision control of high speed ball screw drives[D].Waterloo,Canada:Department of Mechanical Engineering,University of Waterloo,2008.
[7] Houpert L.Ball bearing and tapered roller bearing torque:analytical,numerical and experimental results[C]//Proc of STLE Annual Meeting.Houston,USA,2002:19-23.
[8] Houpert L.Numerical and analtical calculations in ball bearing[C]//Proc of Congres Roulements.Toulouse,France,1999:1-15.
[9]Braccesi C,Landi L.A general elastic-plastic approach to impact analysis for stress state limit evaluation in ball screw bearing return system[J].International Journal of Impact Engineering,2007,34(7):1272-1285.
[10] Hung J P,Wu J S S,Chiu J Y.Impact failure analysis of re-circulating mechanism in ball screw [J].Engineering Failure Analysis,2004,11(4):561-573.
[11]张佐营,宋现春,姜洪奎,等.滚珠丝杠副中滚珠与返向器的碰撞研究[J].中国机械工程,2008,19(7):850-881.Zhang Zuoyin,Song Xianchun,Jiang Hongkui,et al.Research on the impact between balls and re-circulating mechanism in ball screw [J].China Mechanical Engineering,2008,19(7):850-881.(in Chinese)

