可信可控网络中控制节点优化选取算法
张效娟 罗军舟 李 伟
(1青海师范大学计算机学院,西宁 810008)
(2东南大学计算机科学与工程学院,南京 210096)
随着网络技术和应用的迅猛发展,互联网日益呈现出复杂、异构等特点,保证网络的可控性成为当今网络发展的迫切需求,国内外研究人员已陆续开展了相关研究.Greenberg等[1]提出了4D网络控制模型,将网络控制功能从路由器中剥离出来,建立了独立的网络控制层.Caesar等[2]提出并实现了一个路由控制平台,集中实现域内路由决策.林闯等[3]对下一代网络的可信可控关键技术进行了研究,提出了可信可控可扩展的下一代互联网体系结构,同样指出需要构建一个独立的网络控制层面.根据当前国内外对可控网络的研究成果,本项目组在前期研究工作中提出了一种新的可信可控网络模型[4-6],将网络控制与数据传输相分离,形成域内集中、域间分布的控制方式,以提高网络的可控性.但是,域内集中的单一控制节点存在性能瓶颈问题,容易产生单点故障.为了增强网络控制的鲁棒性和可扩展性,一些研究人员提出在域内采用多控制节点进行协同控制的方式,将一个自治域划分为多个控制域,每个控制域有一个控制节点对隶属于该控制域的路由器进行控制,自治域内的多控制节点通过协同控制达到控制决策的一致性.然而,要实现自治域内多控制节点间的协同控制,首先要解决的问题是如何将一个给定网络拓扑的自治域划分成若干控制域,即如何确定每个控制域的管辖范围以及控制节点位置的选取.文献[7]基于4D网络模型,在已知多个候选控制节点位置前提下,给出了控制节点选取及控制域划分的方法,但是其控制节点的候选位置是预先指定的,缺乏合理性.本文基于可信可控网络模型,提出了一种有效的控制节点优化选取算法CNSA(control nodes selection algorithm),无需指定控制节点候选位置,即可实现控制节点的优化选取及控制域的划分.实验结果表明,在相同控制节点规模下,CNSA算法得到的结果在保证控制实时性方面优于文献[7]中的算法.
1 可信可控网络模型

图1 可信可控网络模型
可信可控网络模型通过建立一个独立的控制平面,将网络控制逻辑集中到自治域内的控制节点,由控制节点进行网络控制决策并对网络实施控制,从而实现了网络控制逻辑与数据传输的分离.如图1所示,该模型在不破坏传统TCP/IP网络体系结构的基础上,增加了一个由决策层、观测层、资源层和可信接口层构成的网络控制逻辑结构.资源层通过可信接口层以协议跨层的方式获取各种网络组元及用户行为的状态信息,并提供给观测层,由观测层对其进行描述,以实现网络控制的抽象化,同时为决策层提供一致的网络全局状态可观性视图,保证决策层的高效性和准确性.决策层根据观测层提供的全网可观一致性视图,从系统当前状态以及全局利益最大化的角度出发,进行集中决策并提出相应的控制方案,通过可信接口层提供给TCP/IP网络的各个层面,以达到控制目的.
2 控制节点优化选取算法
集中式的域内控制方式下,单一的控制节点会造成性能瓶颈和单点故障问题,因此在自治域内多控制节点进行协同控制已成为相关研究者的共识[7].可信可控网络将自治域内的控制逻辑集中到域内的控制节点上,为了提高网络控制的可扩展性和鲁棒性,将每个自治域划分成多个控制域,每个控制域中有一个控制节点通过某一路由器接入到网络中,并对隶属于该控制域的所有路由器实施控制,自治域内的多控制节点通过协同控制保证决策的一致性,如图2所示.然而,自治域内实现多控制节点协同控制的首要问题是如何选取控制节点实现控制域的划分,使其既能满足控制实时性的需求,又能降低控制代价.为此,本文提出了一种控制节点优化选取算法,在不需要预先确定控制节点候选位置的情况下,实现对控制域的划分,使得选取的控制节点数目尽量少,并且每个控制节点到所管辖路由器的时延尽量短.
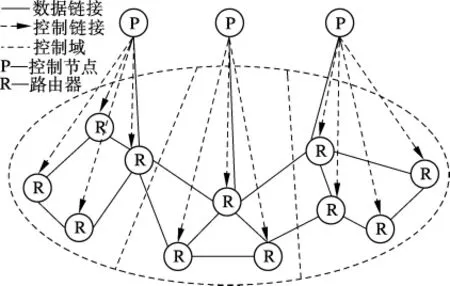
图2 自治域内多控制节点间的协同控制
2.1 算法思想
可信可控网络将给定的自治域划分成多个控制域,每个控制域中设置一个控制节点并通过域内某一路由器接入到网络中,对该控制域内的所有路由器进行直接控制,多控制节点通过协同控制实现一致性决策方案.为了减少因设置控制节点带来的软硬件开销,选取的控制节点应尽量少.同时,控制节点与所管辖路由器之间的时延需要尽可能小,以保证控制的实时性.
本文设定控制节点与所管辖路由器间的最大传输时延为Dmax,自治域内控制节点选取以及控制域划分问题的理想情况是在Dmax的约束下选取最少的控制节点数目,并且路由器到所属控制节点的平均时延最短.由于控制节点需要通过域内的某个路由器接入到网络中,所以控制节点的位置等同于其接入路由器的位置.因此,自治域内控制节点的优化选取问题就是给定一个有n个路由器的网络,将其划分为m个控制域,在每个控制域中确定一个路由器作为控制节点的接入位置,使得每个路由器只隶属于一个控制域.选择的约束条件是使m最小,并且路由器到其对应控制节点的最大时延不超过Dmax且平均时延最短.
2.2 数学模型
自治域G的网络拓扑用无向图G=(V,E)表示,其中V={r1,r2,…,rn},表示G中路由器节点集合,E={e1,e2,…,ek},表示边的集合.控制节点优化选取问题就是将给定的图G=(V,E)划分为m个不相交的节点集 U1,U2,…,Um,其中 Ui∩Uj=∅(i,j=1,2,…,m;i≠j)并且 U1∪U2∪…∪Um=V,在每个节点集Ui中选择一个控制节点Pi对其他的路由器进行控制,控制节点选取的目标为m最小,同时从路由器到其所属控制节点的最大时延不超过Dmax且所有路由器到其所属控制节点的总时延最短.
设二值变量ci表示路由器ri是否被设定为其所属控制域内控制节点的接入点.若ci=1,表示ri为控制节点的接入点,反之,表示ri不是控制节点的接入点.为了简化描述,下面假定ri等同于控制节点.设二值变量δij表示路由器ri是否被控制节点rj控制,δij=1表示 ri受控于 rj,否则表示 ri不受控于rj.令hij表示2个路由器ri和rj之间的最大时延,则自治域内控制节点优化选取问题可转化为如下形式的线性规划问题:

式(1)和式(2)表示2个规划目标,前者为在n个路由器节点中选择最少的节点成为控制节点,后者为同一控制域内所有路由器到所属控制节点的总时延最小;式(3)和式(4)分别定义了2个二值变量;式(5)表示每一个路由器仅被关联到一个控制节点;式(6)保证了每个路由器到其所属控制节点的最大时延不超过设定的阈值Dmax.
2.3 算法描述
2.2节对自治域内控制节点优化选取问题建立了一个多目标约束的线性规划模型,然而该问题是一个NP-hard问题[8].因此,本文提出了根据域内节点间的状况划分控制域并选择控制节点的启发式算法CNSA,主要思想为先选定在Dmax时间内能够到达最多网络中其他路由节点的节点作为控制节点,再将网络中剩余的路由器分配给相应的控制节点构成控制域.将与较多节点传输时延小的节点选为控制节点,能够对周围节点的情况快速感知并做出快速决策,保证网络控制的实时性.
设Ni和Ri分别表示与路由器ri的最大时延小于等于Dmax的路由器的个数和集合,P表示控制节点集合.CNSA算法的主要步骤如下:
①对自治域的每个路由器计算与其最大时延不超过Dmax的路由器的个数,取出当前网络中Nj值最大的节点rj,设定其为控制节点;
②将Rj从拓扑图中删除;
③对剩余的网络拓扑重新计算并选择一个Nj值最大的节点作为控制节点;
④再将Rj从拓扑图中删除;
⑤重复这个过程,直到网络中没有剩余节点.
算法1 控制节点选取算法
1.Generate G=(V,E);
2.While(V!=∅)
3. {For(i=0;i<V.Size;i++)//V.size表示拓扑中节点个数
4. For(j=0;j< V.Size;j++)
5. {If(hij≤Dmax)
6. {Ni++;
7. Ri=Ri∪{rj};}}
8. If Njis max(Ni)
9. P=P∪{rj};//将该节点选为控制节点
10. Delete Rjfrom G;//将该节点及其Dmax时间内可达节点从G中删除
11.}
12.While(1≤i≤n)//为每个路由器选取其相应控制节点
13. {If himis min(hij)(1≤j≤n)
//为每个路由器ri选取时延最小的控制节点
14. δim=1;
15. i++;}
16.Output P,δ;
算法CNSA最终输出的节点集合P即为域内的控制节点集合,δ中包含了每个路由器与相应控制节点的对应关系.算法的第2~11行进行控制节点的选取,其中第3~7行计算每个节点在Dmax时间内可达的节点个数Ni及其能够控制的节点集Ri,第8,9行选取在Dmax时间内可达节点数目最多的节点作为控制节点,第10行将该节点及其控制集从拓扑中删除.然而,上述过程并不能保证在控制节点集为P的情况下,每个路由器都隶属于到其时延最短的控制节点.因此,第12~16行在确定了域内控制节点集为P的基础上对控制域的划分进行了优化,确保每个路由器都被与其相连的最近控制节点控制.
3 实验分析
为了进一步验证和比较CNSA算法的有效性,本文采用了与文献[7]相同的实验拓扑,利用SSFNet仿真工具进行了仿真实验.表1给出了3个自治域内拓扑的属性,其中Lmax表示拓扑中2个节点间的最大时延,Lavg表示2个节点间的平均时延.

表1 实验拓扑属性
首先,在3个不同规模的网络拓扑下,考察选取的控制节点个数随Dmax变化的情况.Dmax值分别设定为5,10,15,20,25,30 ms.从图3 中可看出,控制节点的个数随最大时延的增大而减少,表明CNSA算法是有效的.
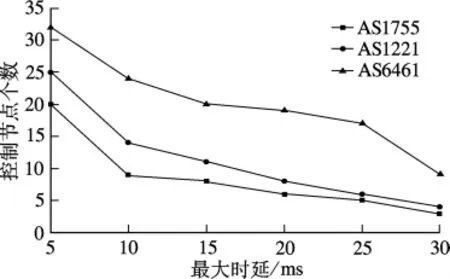
图3 控制节点个数与最大时延的关系
其次,将本文算法CNSA与文献[7]的算法DCNSA进行了比较.仍然采用表1所示的3个AS的拓扑,将在相同控制节点规模下2个算法分别选取的控制节点到路由器的平均时延以及最大时延作为评价指标.在DCNSA算法实验中,将拓扑中的所有路由器位置都设定为候选位置,分别计算不同控制节点规模下的控制节点到路由器的平均时延以及最大时延.由于CNSA中Dmax为输入,控制节点的个数为输出,因此本文将Dmax的值从Lmax以0.5 ms的梯度依次递减,计算控制节点个数与控制节点到路由器的平均时延及最大时延的对应关系,结果如图4所示.由图4可看出,在相同控制节点规模下,2种算法的平均时延接近,但本文算法拥有更小的最大时延.这是因为CNSA选取控制节点时在路由器与控制节点最大时延不超过Dmax的情况下,首先考虑减少控制节点的个数,以降低成本开销,而不是控制节点与路由器间的平均时延.所以,实验结果表明CNSA算法性能优于DCNSA算法.

图4 CNSA算法与DCNSA算法的比较
4 结语
本文针对可信可控网络中自治域内控制节点的选取以及控制域的划分问题,基于图论的思想提出了一种自治域内控制节点优化选取的启发式算法.该算法将控制节点选取问题转换为多目标线性规划问题,以控制节点数目最少和控制节点到所属路由器的总时延最短为优化目标,既能够降低系统软硬件开销,又能够保证控制的实时性;并且实验结果表明CNSA算法是有效的,在相同控制节点规模下,该算法的性能优于已有其他算法.下一步工作是研究自治域内多控制节点如何进行协同以达到高效的一致性控制.
References)
[1] Greenberg A,Hjalmtysson G,Maltz D A,et al.A clean slate 4D approach to network control and management[J].ACM SIGCOMM Computer Communications Review,2005,35(5):41-54.
[2]Caesar M,Caldwell D,Feamster N,et al.Design and implementation of a routing control platform[C]//Proceedings of the 2nd Conference on Symposium on Networked Systems Design and Implementation.Boston,MA,USA,2005:15-28.
[3]林闯,雷蕾.下一代互连网络体系结构研究[J].计算机学报,2007,30(5):693-711.Lin Chuang,Lei Lei.Research on next generation internet architecture [J].Chinese Journal of Computers,2007,30(5):693-711.(in Chinese)
[4]罗军舟,韩志耕,王良民.一种可信可控的网络体系及协议结构[J].计算机学报,2009,32(3):391-404.Luo Junzhou,Han Zhigeng,Wang Liangmin.Trustworthy and controllable network architecture and protocol framework [J].Chinese Journal of Computers,2009,32(3):391-404.(in Chinese)
[5]王鹏,罗军舟,李伟,等.可控网络中多agent系统信念可达性和收敛速度分析[J].软件学报,2010,21(4):782-792.Wang Peng,Luo Junzhou,Li Wei,et al.Analysis on belief reachability and convergence rate of multi-agent system in controllable networks[J].Journal of Software,2010,21(4):782-792.(in Chinese)
[6]谭晶,罗军舟,李伟,等.基于可信度的域间路由机制[J].计算机学报,2010,33(9):1763-1774.Tan Jing,Luo Junzhou,Li Wei,et al.Trust degree based inter-domain routing mechanism[J].Chinese Journal of Computers,2010,33(9):1763-1774.(in Chinese)
[7] Iqbal H,Znati T.Distributed control plane for 4D architecture[C]//Proceedings of IEEE Global Communications Conference.Washington DC,USA,2007:1901-1905.
[8] He Bing,Xie Bin,Agrawal D P.Internet gateway deployment optimization in a multi-channel multi-radio wireless mesh network[C]//Proceedingsof IEEE Wireless Communications and Networking Conference.Las Vegas,NV,USA,2008:2259-2264.

