基于朱氏广义采样定理的射频功放行为建模

翟建锋 张 雷 朱晓维 周健义

(东南大学毫米波国家重点实验室，南京 210096)

在现代无线通信系统中，如WCDMA，CDMA2000，WiMAX和LTE等，数据业务量激增，频谱资源日益稀缺，通常采用效率很高的调制方式，然而这也导致了信号带宽和峰均比增大，比如单载波WCDMA的信号为5 MHz，LTE的信号带宽达20 MHz.在 IMT－Advanced及未来移动通信系统中，射频带宽达100 MHz以上.高峰均比的宽带信号对射频功放的线性度要求很高，通常采用效率很低的功率回退法达到线性度的要求.近年来，功放线性化技术的研究很广泛，常用的线性化技术有前馈法、笛卡儿负反馈法、功率合成法和预失真法等［1］.而在各种线性化技术中，基于功放模型的数字预失真技术备受研究人员的关注.研究人员在射频功放行为建模和数字预失真中广泛采用了多种Voltera 级数模型［2－4］和神经网络模型［5－7］等.

为了建立精确的射频功放行为模型，提高数字预失真的效果，需要对功放的输入和输出信号进行精确的数据采集.功放输出信号含有非线性失真分量，其带宽会扩展为功放输入信号的数倍以上.根据奈奎斯特－香农采样理论，离散系统的采样率必须为信号的最高频率或带宽2倍以上，才能避免混叠现象.如果考虑5阶以上非线性分量，功放输出信号的带宽将非常宽，一般采用很高采样率的ADC才能满足系统采样要求，或者利用其他技术提高采样率和采样带宽，如频率缝补技术［8］、时间交叉多路ADC采样技术等.然而，直接采用高速率的ADC会导致成本大幅度提高;频率缝补技术需要多次采样相同的信号，后期计算处理也相对复杂;时间交叉多路ADC采样技术虽然可以提高ADC的采样率，但会引入多路ADC的幅度误差、相位误差和直流误差等.

本文基于朱式广义采样定理［9－13］，在基于矢量信号源和矢量信号分析仪的2.4 GHz的射频功放平台上，对20 MHz的功放输入输出信号进行数据采集、行为建模验证和数字预失真的仿真分析.实验结果表明，在采样率为输入信号带宽2倍和8倍的情况下，利用有记忆多项式行为建模的归一化均方误差都能达到－41 dB，并且预失真后功放相邻信道泄漏功率比(ACLR)改善均在10 dB以上，达到－45 dBc以下.因此，在100 MHz信号带宽的IMT－Advanced系统中，功放行为建模ADC采样率仅需要输入信号带宽的2倍，即200 MSPS(million samples per second)，就能满足功放建模精度要求，极大地降低了对硬件平台的要求.

1 理论分析

现代无线通信系统中信号带宽越来越宽，射频功放的非线性特性和记忆效应也变得更加复杂.比如在WiMAX系统中，射频信号带宽是20 MHz，基带I和Q信号的带宽为10 MHz，但是功放输出的信号包含非线性失真，其失真后的功率谱带宽远远大于20 MHz，如果考虑3阶、5阶失真分量的话，其带宽分别为60和100 MHz，如图1所示.

根据奈奎斯特－香农采样定理，ADC采样率必须为输入信号带宽的6倍和10倍，才能无混叠地对功放的3阶和5阶非线性分量进行采样.

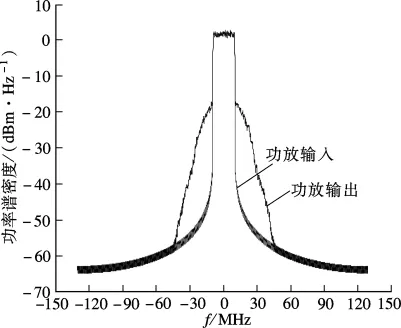
图1 功放输入和输出信号的功率谱比较

朱氏广义采样定理(ZGST)表明，利用输入信号带宽2倍的采样率采集弱非线性系统的输出信号，输出信号就能够重建.ZGST应用条件有:非线性系统中的输入和输出信号为带限，并且非线性系统为一一映射.射频功放可以看成满足ZGST应用条件的弱非线性系统.在功放非线性特性行为建模时，设定ADC采样速率为功放输入信号带宽2倍的速率.然后采集功放的基带输入和输出数据，虽然信号产生了混叠，但仍然可用来建立功放行为模型［11］.因此，利用ZGST定理对功放建模可节约硬件成本、降低采样速率和信号处理复杂度，但缺点是功放输入和输出信号之间的相位校准较复杂［11］.

功放行为模型的建立通常采用Volterra级数法，Volterra级数是泰勒级数的扩展，相当于有记忆的泰勒级数.这里选择有记忆多项式模型作为功放建模和数字预失真的模型，可以看作一种简化的Volterra级数模型.有记忆多项式模型公式如下［4］:

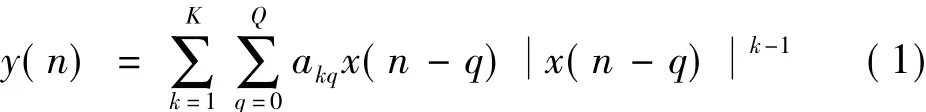
式中，x(n)和y(n)分别表示采样时刻n的功放输入和输出复数信号;akq为模型系数;K为阶数;Q为记忆长度.

因为有记忆的多项式模型的输出信号和模型参数成线性关系，所以可利用简单的最小二乘方法估计参数.假设x(n)和y(n)的数据长度为N，将有记忆的多项式模型表示为矩阵的形式［4］:

其中

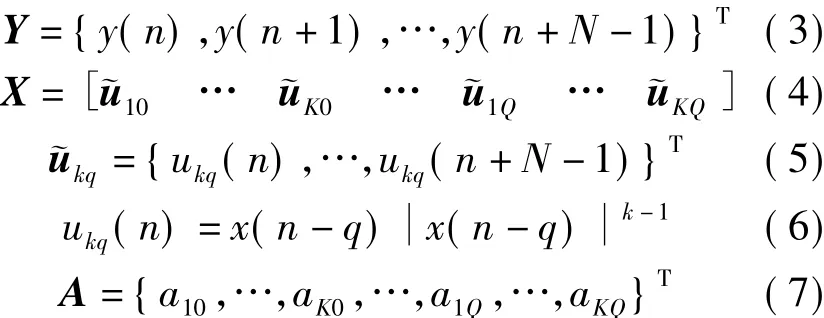
最小二乘解为［4］

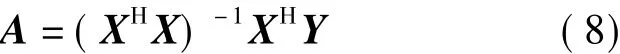
2 实验结果

功放建模的实验平台如图2所示，包括Agi－lent矢量信号源E4438C、Agilent矢量信号分析仪N9030A、射频功放、耦合器、衰减器和Agilent Signal Studio等.功放工作于 AB类，推动功放为AH314，末级功放为 AP561，中心频率 2.4 GHz，输出功率1 W.20 MHz的 WiMAX信号由 Signal Studio软件生成下载到E4438C中，该信号的峰均比约为9 dB.功放的输入和输出信号由N9030A中内置的Agilent 89600软件采样分析，采样率设定为179.2 MSPS.为了信号同步，E4438C的10 MHz参考输出必须连接到 N9030A的参考输入，E4438C上的Event1输出一个脉冲信号作为N9030A的外部触发输入.

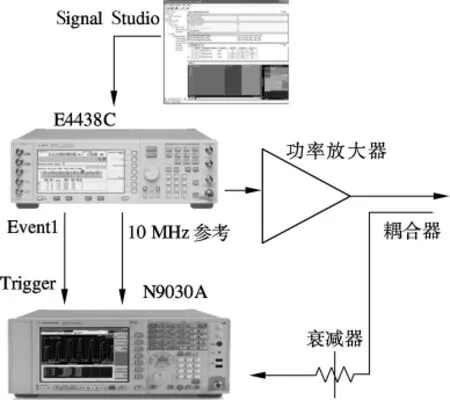
图2 实验平台

功放输入和输出信号同步后，利用有记忆的多项式模型建立功放的行为模型，取记忆长度为4，阶数为5.建模时利用最小二乘法，取1.0×104点输入和输出数据提取模型参数，然后取不同的数据进行模型验证.功放的幅度和相位的失真特性如图3所示，可看出功放有明显的记忆效应.

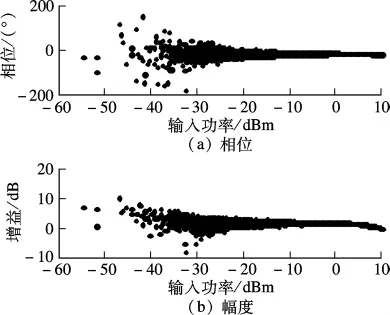
图3 功放的幅度和相位特性

在8倍过采样的情况下，即采样率为179.2 MSPS时，功放测量输出信号和模型误差的功率谱密度比较如图4(a)所示，图中模型误差信号的功率谱密度低于功放输出信号的功率谱密度40 dB以上，其建模的归一化均方误差达到－41 dB.

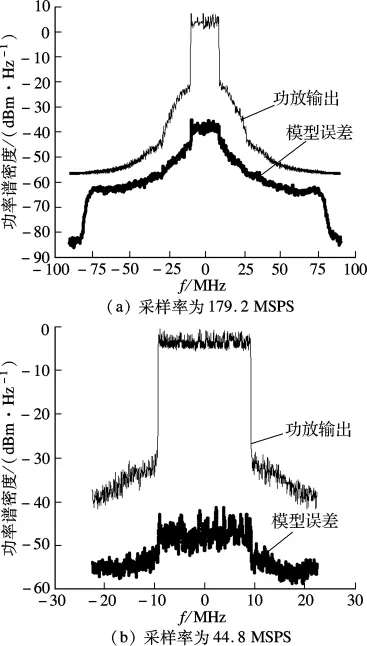
图4 功放输出和模型误差功率谱密度比较

根据朱氏广义采样定理，利用功放输入信号带宽2倍的采样率(44.8 MSPS)采样功放的输出数据，就可建立功放的行为模型并提取非线性特性.在实验中，Agilent矢量信号分析仪在采样数据前会利用数字滤波器滤除大于奈奎斯特频率的部分，这样会导致带外频谱信息的丢失，包括混叠信息，然而，朱氏采样定理应用时必须考虑足够大的带宽［12］，因此不能直接在Agilent 89600软件中设定采样率为44.8 MSPS，必须先高倍过采样然后降采样抽取得到功放的输入和输出数据.图4(b)显示了采用上述方法降低采样率到44.8 MSPS的情况下，功放输出信号和模型误差的功率谱密度比较结果，其建模的归一化均方误差也达到－41 dB左右.图5显示了2倍采样率建模情况下，900个采样点的功放输出I和Q时域信号与模型误差的比较结果，图中模型误差远远小于I和Q信号.

图5 功放输出与模型I和Q信号比较(44.8 MSPS)

另外，利用有记忆的多项式，建立功放的逆模型作为数字预失真的模型，先把原始功放输入数据进行预失真，再通过功放模型进行数字预失真的仿真.在2倍采样率的情况下，先把功放2倍采样率的输入信号插零到179.2 MSPS后，通过预失真模型得到179.2 MSPS采样率的宽带预失真信号，再通过功放模型进行数字预失真的仿真［11］.图6显示了在2倍采样和8倍过采样的情况下，功放预失真前后功率谱密度仿真比较结果，可看出在这2种情况下，预失真后ACLR都可以改善10 dB以上，达到－45 dBc以下.

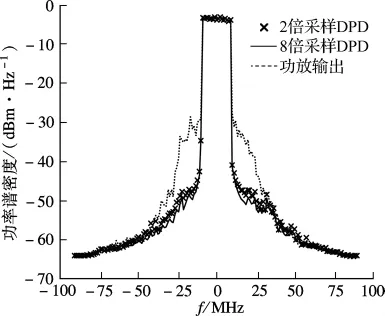
图6 功放预失真前后功率谱密度比较

3 结语

本文分析了朱氏广义采样定理在射频功率放大器行为建模中的应用.在基于Agilent仪器和2.4 GHz射频功放的实验平台上，输入20 MHz的WiMAX信号，对功放输入和输出信号进行数据采集和行为建模验证，最后进行了预失真仿真.本文选择有记忆多项式建立功放行为模型和预失真模型，利用朱氏广义采样定理，在降低ADC采样率和过采样情况下，比较了模型的归一化均方误差.模型验证结果表明，在2倍采样和8倍过采样的情况下，有记忆多项式行为建模的归一化均方误差均达到－41 dB左右.预失真结果表明功放在上述2种情况下ACLR均改善10 dB以上，达到－45 dBc以下.

References)

［1］ Kenington P B.High linearity RF amplifier design［M］.Boston，MA:Artech House，2000.

［2］ Zhu A，Wren M，Brazil T J.An efficient Volterrabased behavioral model for wideband RF power amplifiers［C］//Proceedings of the IEEE International Microwave Theory and Techniques Symposium.Philadelphia，PA，USA，2003，2:787－790.

［3］Schetzen M.The Volterra and Wiener theories nonlinear systems［M］.New York:Wiley，1980.

［4］ Ding L，Zhou G T，Morgan D R，et al.A robust digital baseband predistorter constructed using memory polynomials ［J］.IEEE Transactions on Communications，2004，52(1):159－164.

［5］ Liu T J，Boumaiza D R，Ghannouchi M.Dynamic behavioral modeling of 3G power amplifiers using real－valued time－delay neural networks［J］.IEEE Transactions on Microwave Theory and Techniques，2004，52(3):1023－1033.

［6］ Lee K C，Gardner P.Neuro－fuzzy approach to adaptive digital predistortion ［J］.Electron Letters，2004，40(3):185－186.

［7］ Zhai J F，Zhou J Y，Zhang L，et al.Dynamic behavioral modeling of power amplifiers using ANFIS－based Hammerstein［J］.IEEE Microwave and Wireless Components Letters，2008，18(10):704－706.

［8］Wisell D，Ronnow D，Handel P.A technique to extend the bandwidth of an RF power amplifier test bed［J］.IEEE Transactions on Instrumentation and Measurement，2007，56(4):1448－1494.

［9］ Zhu Y M.Generalized sampling theorem［J］.IEEE Transactions on Circuits and Systems，1992，39(8):587－588.

［10］ Frank W A.Sampling requirements for Volterra system identification［J］.IEEE Signal Processing Letters，1996，3(9):266－268.

［11］ Zhu A，Draxler P J，Yan J J，et al.Open－loop digital predistorter for RF power amplifiers using dynamic deviation reduction－based Volterra series［J］. IEEE Transactions on Microwave Theory and Techniques，2008，56(7):1524－1534.

［12］ Wisell D，Handel P.Implementation considerations on the use of Zhu’s general sampling theorem for characterization of power amplifiers［C］//Conference Record—IEEE Instrumentation and Measurement Technology Conference.Warsaw，Poland，2007:4258472.

［13］ Andersen O，Bjorsell N，Keskitalo N.A test－bed designed to utilize Zhu’s general sampling theorem to characterize power amplifiers［C］//International Instrumentation and Measurement Technology Conference.Singapore，2009:201－204.