基于随机理论的汇流影响因素分析

韩晓峰

(齐齐哈尔松嫩水利建筑工程有限责任公司，黑龙江齐齐哈尔161006)

水文模拟的理论基础是产汇流理论。大量的实测资料表明，在产汇流过程中，存在着许多难以预测和控制的随机性因素。概括起来主要表现在:①水文模型描述的降雨－径流、河道洪水演算等过程都是建立在物理简化的基础上的，这就导致了模型结构的不确定性;②降雨时空分布和下垫面时空分布的不均匀性，以及水文资料或信息的不确定性等，导致了模型输入的不确定性;③大多数水文模型的参数主要是依据降雨和径流资料来率定，由于资料的选取、优化方法、目标函数及参数组合等因素而产生了模型参数的不确定性。这些不确定性因素始终存在并制约着防洪决策的正确性，目前广泛采用的水文模型，认为其结构、模型的输入及参数都是确定性的，即对于一个流域系统来说，认为系统响应是唯一的，这显然是不符合实际情况的。针对自然界中存在的许多随机不确定现象，用包含随机元素的随机微分方程建立和模拟其过程将更为优越。本文应用随机微分方程对水文过程中的随机不确定因素进行分析和探讨。

1 理论依据

线性水库的随机汇流系统可表达为:

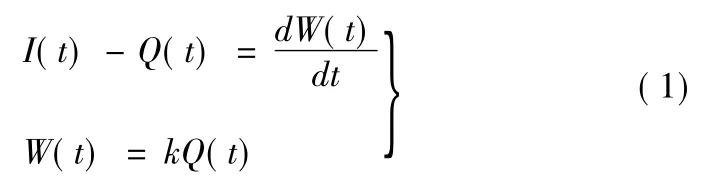
式中:I(t)为汇流系统的输入;Q(t)为汇流系统的输出;W(t)为汇流系统的蓄量;k为线性水库的蓄量常数。图1为线性水库示意图。

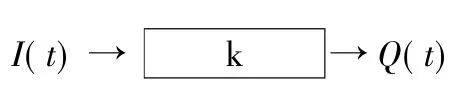
图1 线性水库示意图

联立上述两式可得:

式(2)是汇流系统结构、参数及其输入均为确定性时描述汇流过程的微分方程式。考虑汇流过程中的随机不确定性，可进行如下处理:

1)线性水库的随机输入过程。对于一个稳定的水文系统，有效降雨分布或河道上断面流量在输入时可考虑成一个随机过程I(t)，则在流域出口断面形成相应的随机出流过程Q(t)。考虑随机输入过程为马尔可夫过程，可以认为，输入的随机过程是在其均值(t)的基础上，叠加一个高斯白噪声过程，即

式中: (t)为t时刻入流的均值;w(t)为t时刻输入的高斯白噪声过程，它具有零均值，且=w(t)，B(t)为维纳过程或布朗运动，属于高斯随机过程。

则式(2)可改写为:

微分方程式(4)引入了输入随机项之后，即为具有随机输入项的随机汇流模型，根据随机微分方程理论，可解得出流过程的均值和方差为

2)参数的随机不确定性。汇流系统中包含的参数在传统的汇流计算中，都是作为确定性值来考虑的。但是模型参数由于受众多随机性因素的影响，也具有一定的随机性，各次洪水求出的模型参数可认为是其随机性的具体表现。

根据定义，入流为单位函数时，其出流过程为S曲线。则根据式(2)可得S曲线的表达式为:

将式(7)中的参数α视为随机变量，则根据随机参数的随机特性可确定随机S曲线的统计特性，从而得到出流过程的各种统计特性。假定α服从正态分布，则有:

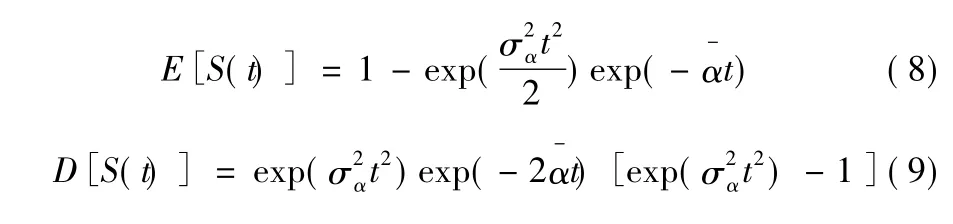
3)同时考虑输入和参数均为随机的情形。在方程式(4)中考虑参数k为随机变量，则由随机微分方程理论可知，式(4)是一个典型的It0方程，它具有随机初始条件、随机系数和随机输入项。这里采用建立矩方程来确定随机出流过程的均值和方差。解得出流过程的一阶原点矩和二阶原点矩为:

则方差可由D(Q(t))=E(Q2(t))－(E(Q(t)))2计算得到。

式中:D为入流过程强度;其它符号意义同前。

2 入流过程处理

在实际应用中，由于入流过程不是连续的函数形式，一般用离散数值的形式给出。因此，如果模型的入流过程可以分解成若干项之和，则总的入流过程所形成的出流过程必等于各分项入流过程所形成的出流过程之和。对于一个线性流域系统来说，我们可以把入流过程假设由一些简单的基本函数组成，例如单位函数、脉冲函数等。这说明，欲求一般形状的入流过程所形成的出口断面流量过程，可首先求出简单入流过程所形成的出流过程。

本文算例中模型输入均值直接采用实测值，用单位入流函数给出其近似表达式如下:

3 模拟结果分析与讨论

针对上述3种情况，以湖南柘溪水电站下游江南～夫溪河段为例讨论各种因素对汇流系统出流过程的影响。

湖南柘溪水电站下游江南～夫溪河段长L=20.1 km，波速为Ck=2.430～2.792 m/s，其入流资料见表1。试推求1967年5月13日～14日洪水的夫溪出流过程的均值和方差。

3.1 参数和初始值的确定

1)具有随机输入过程的情况。根据河段长L=20.1 km，波速为Ck=2.430～2.792 m/s，可得该河段的蓄量常数为k=2.3 h，取计算时段Δt=0.5 h。根据水文测验规范规定的精度要求，假设输入过程的变差系数约为0.05，即相对均方误差为5%，初始出流过程为确定性量，即E[ Q (t0) ] =0，D[ Q (t0) ] =0。

2)参数为随机变量的情况。蓄量系数均值取k=2.3 h，即α=0.435 h－1，变差系数为0.15，即蓄量系数的均方差为σα=0.0653 h－1。

3)参数和输入均为随机的情况。假定蓄量系数服从正态分布，即α～N(0.435，0.0019)。在河道洪水演算中，其输入为上断面的流量，误差主要来源于测验误差，因此这里仍以实测流量作为均值过程，变差系数为0.1，并假定任一时刻的入流量服从实测值为均值，变差系数为0.1的正态分布。

3.2 结果分析

初始条件确定以后，根据式(5)和式(6)计算具有随机输入的出流过程的均值和方差，根据式(8)和式(9)计算具有随机参数的出流过程的均值和方差，根据式(10)和式(11)计算参数和输入均为随机的出流过程的均值和方差，具体计算结果见表1。

表1给出了各种随机性因素影响下的江南－夫溪河段一次洪水出流过程的均值和均方差。从表1数据可以看出，3种情况下计算得到的均值过程相差不大，这主要是因为本次采用的模型为一个线性水库模型，其蓄量调节能力稍差，但对于给河段的计算满足精度要求。从计算得到的均方差过程可以看出，输入随机不确定性对预报的影响大于参数随机不确定性对预报的影响。这是因为对于具有随机系数的出流过程的方差主要取决于蓄量系数的变差系数，本次计算中，江南－夫溪河段随机参数的变差系数为0.15，而参数和输入均为随机时的变差系数为0.1，导致随机参数情况下计算的均方差偏大，这说明预报的不确定性增大了，因此，随机蓄量系数的变化大小直接影响着洪水出流过程的不确定性程度。

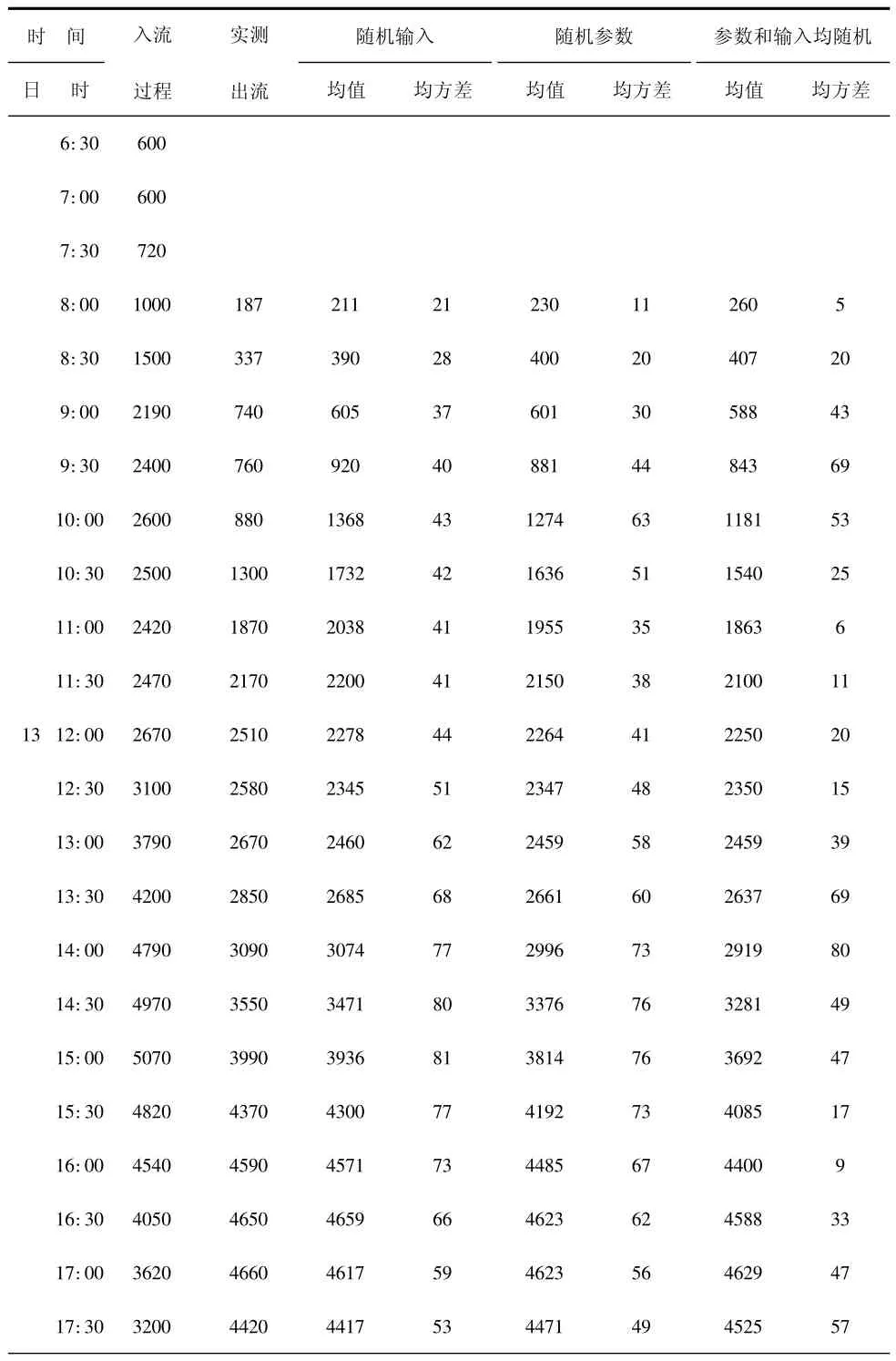
表1 江南－夫溪河段出流过程模拟计算成果表 m3/s

4 结论

1)考虑各种随机性因素对汇流系统出流过程的影响，可以同时给出汇流系统出流过程的均值及均方差过程，从而确定各种需要的出流过程的统计特性，为防洪决策提供依据。结果表明，具有随机系数的出流过程的方差主要取决于蓄量系数的变差系数，随机蓄量系数的变化大小直接影响着洪水出流过程的不确定性程度。

2)考虑各种不确定性对出流过程的影响，可以为防洪决策、降低风险提供了有价值的不确定度。考虑随机性因素的影响建立的汇流模型，得到的出流过程不再是一个确定性的数值，而是服从某种分布的概率形式。这对进行洪水的概率预报等会有所帮助。

3)本文仅以线性水库为例，分析探讨了影响汇流过程的随机不确定性因素，对于更复杂的流域汇流系统还有待于进一步深入研究。

［1］芮孝芳.水文学原理［M］.北京:中国水利水电出版社.2004.

［2］孙颖娜，王红星，惠琳.流域汇流系统随机不确定性分析［J］.黑龙江大学工程学报，2011，2(2):16－18.

［3］Krzysztofowicz，R.，Maranzano，C.J.Bayesian system for probabilistic stage transition forecasting［J］.Journal of Hydrology，2004(299):15－44.

［4］赵仁俊.流域水文模型的比较分析研究［J］.水文，1989(6):1－5.

［5］谢平，胡彩霞，谭莹莹，等.西江归槽洪水研究进展［J］.黑龙江大学工程学报，2011，2(1):29 －33.

［6］任立良，刘和远，袁飞.水文学演进历程的特征剖析［J］.黑龙江大学工程学报，2011，2(1):24 －28.

［7］郭生练，李兰，曾光明.气候变化对水文水资源系统影响评价的不确定性分析［J］.水文，1995(6):8－14.

［8］张洪刚，郭生练，何新林，等.水文预报不确定性的研究进展与展望［J］.石河子大学学报(自然科学版)，2006，24(1):15－21.

［9］孙颖娜，芮孝芳.随机输入情况下汇流计算方法的探讨［J］.水科学进展.2005，16(5):661－665.