多层次半结构性多目标模糊优选理论在赣江流域水量分配中的应用

程孟孟，陈 进

（长江科学院a.水资源综合利用研究所；b.院长办公室，武汉 430010）

多层次半结构性多目标模糊优选理论在赣江流域水量分配中的应用

程孟孟a，陈 进b

（长江科学院a.水资源综合利用研究所；b.院长办公室，武汉 430010）

随着人口的增长和经济的发展，生活和生产需水日渐增多，水资源供需矛盾日益突出，而用水效率低、用水浪费现象也没有得到有效的控制。我国水资源当前所面临的严峻形势要求我们必须对水资源进行公平而合理的分配，提高水资源的利用效率，缓解供需矛盾。首先构建了多层次半结构性多目标模糊优选模型，并以赣江为例，用该模型对其水资源在各用水区域之间进行了分配，旨在对这种水量分配方法进行探讨和实践，以期为赣江流域水量分配工作提供一种可行的参考方法。

多层次半结构性多目标模糊优选；水量分配；赣江流域

1 概 述

随着人口的增长和经济的发展，人类对水资源的需求量日益增加，人类与环境、人类不同区域、区域不同行业间的用水矛盾日益突出，同时用水效率低、用水浪费现象也没有得到很好的解决［1］。我国水资源当前所处的形势要求我们必须对水资源进行合理分配，兼顾人类用水和环境用水，协调不同区域、区域不同行业间的用水矛盾，提高用水效率，实现水资源的可持续利用。

多目标半结构性模糊优选理论已经在水资源系统、农业系统等中得到了良好的应用。陈守煜［2］（1990）提出了多阶段多目标决策系统模糊优选理论，并将其应用于水资源量的最优分配之中；陈守煜［3］（1994）将模糊优选与模糊关系有机结合起来，提出了多目标系统模糊关系优选决策理论，并将其应用于多目标农业系统最优耕作方式的确定之中；陈守煜、丁晓阳［4］（2003）将多目标半结构性决策模糊识别理论与模型应用于东北地区北水南调最优调水方案的确定之中。

水量分配的方法有很多种，鉴于取用和用水的不确定性，本文采用模糊数学的方法，在已有研究的基础上，以多目标半结构性模糊优选理论为基础，建立水量分配多层次半结构性多目标模糊优选模型，并以赣江为例，对该模型进行了应用。

2 水量分配多层次半结构性多目标模糊优选模型

水量分配问题是一个涉及多目标、多地区的复杂分配问题，涉及到社会、经济、环境等多种因子［5］，而且取水和用水存在很大的不确定性，因此方案的优选具有模糊性和相对性的特点。多层次半结构性多目标模糊优选理论主要应用于复杂系统方案的优选，由于模糊关系描述了系统事物之间的普遍联系，因此该理论具有广泛的通用性，可以为流域水量分配工作服务。

2.1 模型构建

2.1.1 指标体系的建立［6，7］

水量分配以公平性为首要原则，在公平的基础上尽可能满足高效率用水地区的用水需求，同时水量分配必须兼顾近期与远期用水、当代与后代用水，以实现水资源的可持续利用。因此，本文构建了4层指标体系，如图1所示。最高层为水量在各地区间的分配；第1层为公平性、高效性和可持续性3大原则；第2层为用水规模、水量贡献等5个目标；第3层又细化为人口数量、农田有效灌溉面积等10个指标。

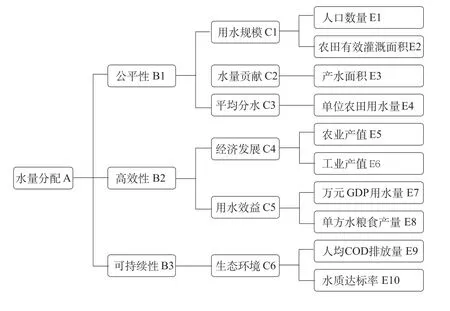
图1 水量分配指标体系Fig.1 System of water allocation indicators

2.1.2 模型原理水量分配系统也可看成是由公平、高效、可持续

3个子系统组成，这3个子系统可分解为3个3层模糊优选系统。水量分配多层次半结构性多目标模糊优选模型的原理是分别对3个子系统建立多层系统模糊优选模型，得到3个子系统的系统计算输出，并把这些输出作为最后一层的输入，然后确定水量分配到各地区的相对优属度，进行归一化，得到各地区的分水权重，再用可分配水资源总量与各地区权重相乘，最后得到各地区分配到的水量。子系统的系统计算输出是由下往上逐层推进的，第3层的输出作为第2层的输入，第2层的输出作为第1层的输入，最后得到子系统的输出。

2.2 多层系统半结构性多目标模糊优选理论［8－10］

2.2.1 目标权重的确定

设目标集P＝｛p1，p2，…，pm｝，pi为第i个目标，i＝1，2，…，m；m为目标总数。

目标集P中的目标就“重要性”进行二元对比的定性排序。首先确定排序标度：若pk比pl重要，令排序标度ekl＝1，elk＝0；若pk与pl同样重要，令ekl＝0.5，elk＝0.5；若pl比pk重要，令排序标度ekl＝0，elk＝1。k＝1，2，…，m；l＝1，2，…，m。根据排序标度的确定规则，得到目标集二元对比重要性排序标度矩阵

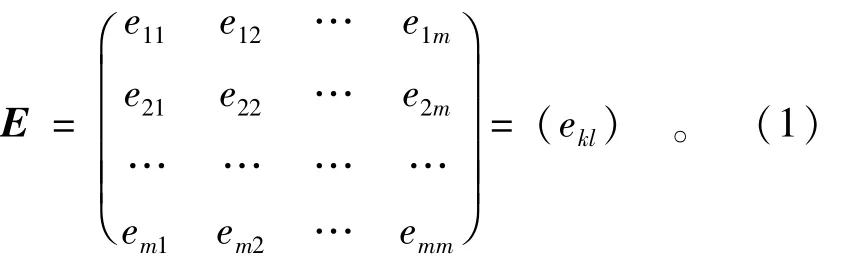
将各行和数由大到小排列，给出目标集关于重要性的定性排序。以和数最大的行所对应的目标为准，分别与其余目标进行重要性比较。在进行重要性比较时，若同样重要，则模糊标度赋值0.5，若无可比拟的重要，则模糊标度赋值1.0。按照我国的语言习惯，在同样与无可比拟之间插入9个语气算子，共同构成10个语气算子级差，因此，在0.5与1之间，以线性增值0.05，插入9个模糊标度值。然后根据公式（2）计算出相应的隶属度值

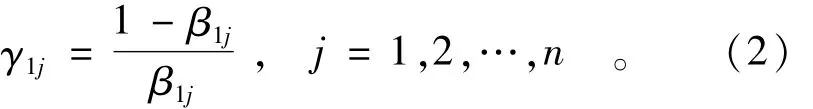
式中：β1j为排序第1位目标与第j位目标相比对于优的模糊标度值；γ1j为排序第1位目标与第j位目标相比对于优的隶属度值。

也可以查表1得到，然后对其归一化得到目标集的权重。

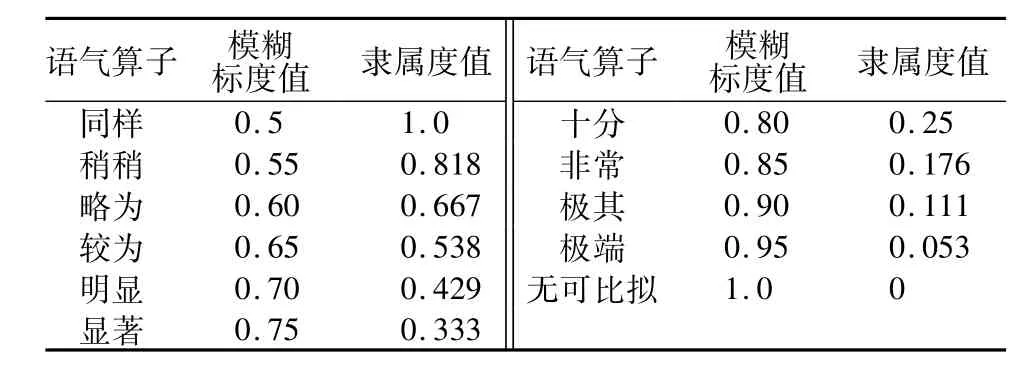
表1 语气算子与模糊标度、相对隶属度对应关系Table 1 Corresponding relationship of semantic operators w ith fuzzy scale and relativemem bership degree

2.2.2 定量目标相对优属度公式

越大越优定量目标的相对优属度计算公式为

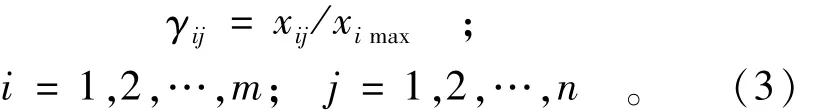
式中：xij为j决策i目标的值；γij为j决策i目标的相对优属度。

越小越优定量目标的相对优属度计算公式为

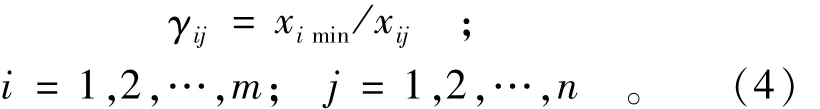
式中：xij为j决策i目标的值；γij为j决策i目标的相对优属度；xij≠0。

2.2.3 定性目标相对优属度的确定

首先对决策集D关于定性目标C按照优越性进行二元对比的定性排序，就定性目标C而言，若Dk比Dl重要，令排序标度ekl＝1，elk＝0；若Dk与Dl同样重要，令ekl＝0.5，elk＝0.5；若Dl比Dk重要，令排序标度ekl＝0，elk＝1。k＝1，2，…，n；l＝1，2，…，n。得到决策集D关于定性目标C的二元对比重要性排序标度矩阵

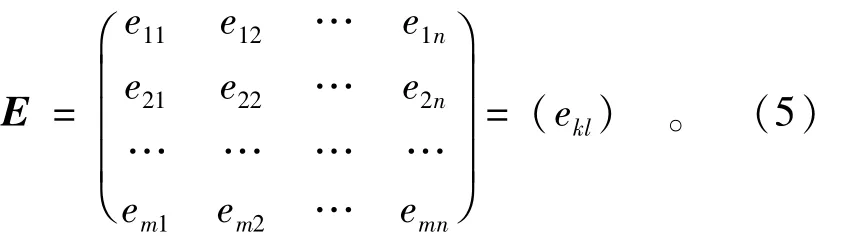
将各行和数由大到小排列，得到决策集关于优越性的定性排序。以和数最大的行所对应的决策为准，分别与其余决策进行优越性比较，查表1确定决策集D关于定性目标C的相对优属度。

2.2.4 决策集相对优属度的确定

设方案j以相对优属度μj隶属于理想方案，以相对劣属度μcj隶属理想劣方案，根据模糊集补集定义，有

考虑m个目标的权重不同，设目标权向量

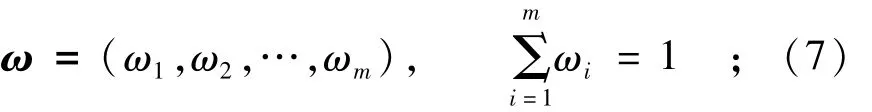
方案j与理想优、劣方案的广义权距离分别为：

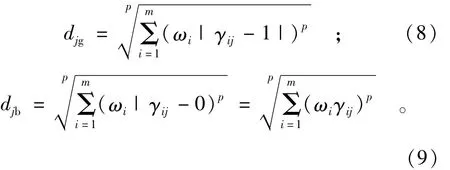
μj的最优解计算公式为

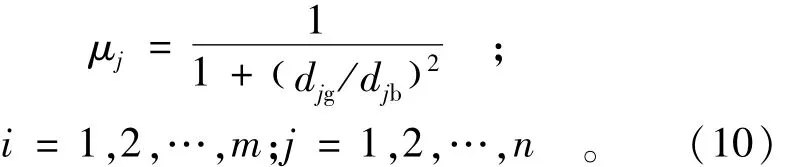
式中：μj为方案j的相对优属度；ωi为目标权重；γij为j决策i目标的相对优属度；p为参数，p＝1时，djg，djb为海明距离；p＝2时，djg，djb为欧式距离。

2.2.5 多层系统模糊优选

本文构建的模糊优选系统可分解为3层，如图2所示。第1层为若干并列子系统（称为单元系统），每个单元系统均有若干个指标特征值输入，如第1个单元系统有2个指标特征值输入，第2个单元系统有1个指标特征值输入。首先确定指标集的权重和相对优属度，并将其作为第1层的输入，采用决策集优属度的计算公式计算第1层各单元系统的相对优属度，与其权重共同作为第2层各单元系统的输入，同样采用决策集优属度的计算公式计算第2层各单元系统的相对优属度，与其权重共同作为第3层的输入，输出即为第3层各单元系统的相对优属度，归一化即为分水权重。

图2 3层模糊优选系统Fig.2 Fuzzy optim ization system by three layers

表2 C1分系统目标权重、相对优属度表Table 2 Objective weight and relative optimalmembership of C1 subsystem

表3 B1分系统目标权重、相对优属度表Tab le 3 Objective weight and relative optimalmem bership of B1 subsystem

3 实 例

3.1 赣江流域概况

赣江流域水资源丰富，但是随着江西工业化的快速推进，一些污染型企业将未经处理的污水直接排入赣江及其支流，沿江市镇的生活污水、生活垃圾以及农业生产中面源污染都汇入赣江，使赣江水质下降，可用水资源逐渐减少。同时，随着流域经济的发展和人口的增加，生产、生活、生态用水量都急剧上升。若不对赣江流域水资源进行合理的分配，强化用水管理，赣江也将面临缺水问题。

江西省从赣江流域取用水资源的地级市有赣州市、吉安市、新余市、萍乡市、宜春市、南昌市、抚州市，因此决策集D＝（d1，d2，d3，d4，d5，d6，d7）。选择2030年为规划水平年，由于可获得的资料有限，对赣江流域的水量分配仅考虑公平性和高效性2个子系统。

3.2 确定赣江流域水量分配方案

确定E1，E2的相对优属度和权重，得表2。

利用式（10），其中参数p＝1，djg，djb为海明距离，计算出C1关于7个地区对于优的相对优属度γ21＝（0.997，0.885，0.031，0.004，0.504，0.169，0.001）。

按照同样的方法确定C2，C3的相对优属度，并确定C1，C2，C3的权重，得表3。

据表3计算出B1关于7个地区对于优的相对优属度γ11＝（1.000，0.984，0.205，0.168，0.692，0.321，0.158）。

类似于公平性子系统B1相对优属度的确定方法，计算出B2关于7个地区对于优的相对优属度γ12＝（0.993，0.959，0.504，0.378，0.745，0.945，0.399）。

确定B1，B2的权重W＝（0.65，0.35）。然后结合B1，B2的相对优属度向量，计算得到最高层关于7个地区对于优的相对优属度向量，归一化得到7个地区的分水权重W＝（0.264 0，0.263 9，0.044 3，0.024 3，0.226 4，0.152 8，0.024 4）。

因此，赣州市、吉安市、新余市、萍乡市、宜春市、南昌市、抚州市的分水量分别占赣江流域水资源可分配总量的26.40%，26.39%，4.43%，2.43%，22.64%，15.28%，2.44%。

3.3 合理性分析

以2005年为参照年，选择现状用水指标——人口、经济条件和用水量分别与分水量的计算值进行比较。首先对现状用水指标进行统计，如表4所示，其中，人口指的是各地区人口数量占赣江流域总人口的比例；经济指的是各地区工农业产值占赣江流域工农业总产值的比例；用水量指的是各地区现状用水量占赣江流域可分配水资源总量的比例。然后，绘制折线图，对现状用水指标与分水量的计算值进行比较，如图3所示。

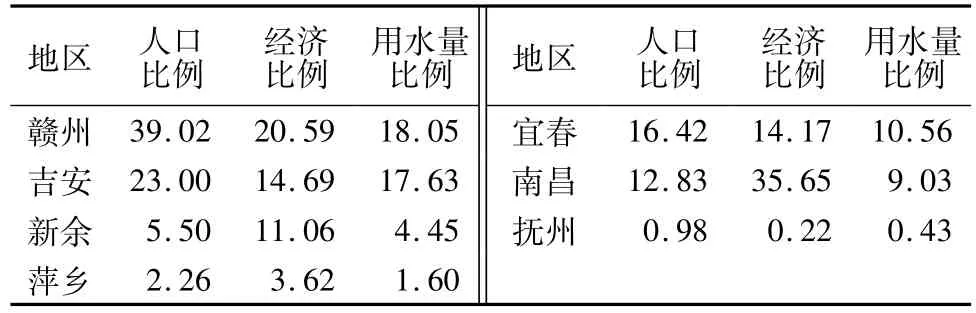
表4 赣江流域各地区现状用水指标Table 4 Indices of current water use in each region of Ganjiang River Basin %

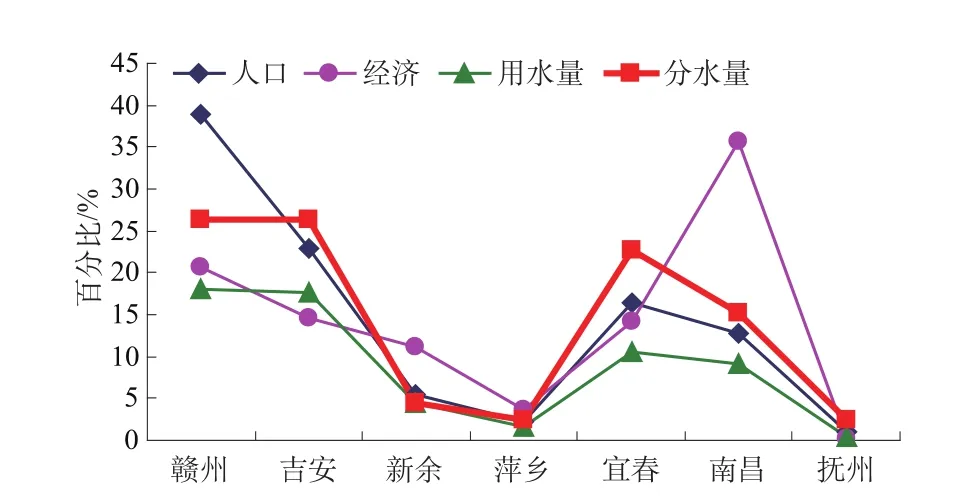
图3 各地区分水量与现状用水指标比较Fig.3 Com parison of water allocation results and current water use indices

总体来看，分水量总体变化趋势是合理的。图3显示，各地区分水量与人口、经济和用水量基本呈正相关关系，人口多、经济条件好、现状用水量大的地区，分水量也比较大。但是南昌市经济条件居各地区之首，分水量却低于部分地区，这与南昌市的实际情况并不矛盾。首先，南昌市人口数量相对比较少，决定了生活需水量比较少；其次，南昌市的工业在国民经济生产中所占的比重远高于农业，而工业用水效率远高于农业。因此南昌市需水量相对比较小，分水量就自然比较少。

在人口、经济和现状用水量3项指标中，现状用水量与分水量的相关性最好，也具有其合理性，因为用水量是所有用水指标的综合反映，也是合理预测未来用水的基础和重要参考因素，在一定程度上反映了未来用水量的大小。

另外，各地区分水量均高于现状用水量，因此，未来用水可以在现状用水水平的基础上新增用水需求，以满足人口增长、经济发展所提出的新的需求。

综上所述，该水量分配方案是合理的。

4 结 论

水量分配问题是一个涉及多目标、多地区的复杂分配问题。鉴于来水和用水的不确定性，本文基于模糊数学理念，构建了多层次半结构性多目标模糊优选模型。该模型以公平性、高效性、可持续性为原则，在公平性原则下建立了用水规模等3个指标，在高效性原则下建立了经济发展、用水效率等2个指标，在可持续性原则下建立了生态环境1个指标。再对上述指标进行细分，最终得到10个分指标。

通过对一个应用示例的运算说明，只要能够获得准确的数据资料，运用半结构性多目标模糊优选模型对流域水资源在各个地区之间分配是可行的。本文建立的水量分配指标体系并非一成不变的，在实际的运用中，可根据流域的实际情况和可获得的资料进行添加或删减。

对流域水资源在各个用水区域之间进行分配是水量分配的第一步，本文下一步需要做的工作是对各地区分得的水量在不同行业之间进行分配，确定农业、工业、生活、生态环境等用水户的分水量，以便对用水进行更好的管理。

［1］ 雷 声，杨永生，许新发，等.江西省“五河”流域水量分配数学模型研究［J］.江西水利科技，2009，35（1）：6－10，50.（LEISheng，YANG Yong-sheng，XU Xin-fa，et al.Research on the Mathematical Model of Water Quantity Distribution of Five Rivers Basin in Jiangxi Province［J］.Jiangxi Hydraulic Science＆Technology，2009，35（1）：6－10，50.（in Chinese））

［2］ 陈守煜.多阶段多目标决策系统模糊优选理论及其应用［J］.水利学报，1990，（1）：1－10.（CHEN Shou-yu.The Theory and Application of Fuzzy Optimum Selection for the Multistage and Multiobjective Decision Making System［J］.Journal of Hydraulic Engineering，1990，（1）：1－10.（in Chinese））

［3］ 陈守煜.多目标系统模糊关系优选决策理论与应用［J］.水利学报，1994，（8）：62－66，71.（CHEN Shouyu.Theory of Optimal Decision Making for Fuzzy Relationship in Multiobjective Systems and Its Applications［J］.Journal of Hydraulic engineering，1994，（8）：62－66，71.（in Chinese））

［4］ 陈守煜，丁晓阳.多目标半结构性决策模糊识别理论在北水南调中的应用［J］.水资源保护，2003，（1）：29－35.（CHEN Shou-yu，DING Xiao-yang.Application of Multi-objective and Semi-structural Decision-Making Fuzzy Recognition Theory to the North-to-South Water Diversion Project［J］.Water Resources Protection，2003，（1）：29－35.（in Chinese））

［5］ 何俊仕，李秀明，尉成海，等.大凌河流域水量分配方法研究［J］.人民黄河，2008，30（4）：50－51，54.（HE Jun-shi，LIXiu-ming，YU Cheng-hai，et al.Water Allocation Schemes for Daling River Basin［J］.Yellow River，2008，30（4）：50－51，54.（in Chinese））

［6］ 姜 玮，周良雄.层次分析决策法在水量分配中的应用［J］.湖南水利水电，2009，（1）：49－51.（JIANG Wei，ZHOU Liang-xiong.Application of Level Analysis and Decision Method in Distribution of Water Quantity［J］.Hunan Hydro＆Power，2009，（1）：49－51.（in Chinese））

［7］ 鲍燕寒，徐得潜，储德义，等.层次分析法在淮河干流水量分配中的应用［J］.工业用水与废水，2009，40（6）：60－61，89.（BAO Yan-han，XU De-qian，CHU De-yi，etal.Application of Analytic Hierarchy Process in Water Quantity Allocation of Huaihe River Mainstream［J］.IndustrialWater＆Wastewater，2009，40（6）：60－61，89.（in Chinese））

［8］ 陈守煜.多目标系统半结构性决策理论与方法［J］.辽宁工程技术大学学报，2001，20（5）：578－582.（CHEN Shou-yu.Semi-structural Decision-making Theory and Approach for Multi-objetive System［J］.Journal of Liaoning Technical University，2001，20（5）：578－582.（in Chinese））

［9］ 葛 敏.水权初始分配模型探讨［D］.南京：河海大学，2004.（GE Min.Study on Models of Water Rights Initial Allocation［D］.Nanjing：Hohai University，2004.（in Chinese））

［10］陈守煜.工程水文水资源系统模糊分析理论与实践［M］.辽宁：大连理工大学出版社，1998：117－125.（CHEN Shou-yu.The Fuzzy Sets Theory and Practice for Engineering Hydrology and Water Resources System［M］.Liaoning：Dalian University of Technology Press，1998：117－125.（in Chinese） ）

（编辑：姜小兰）

Application of Sem i-structural and M ulti-objective Fuzzy Optimal Selection Theory to W ater Allocation in Ganjiang River Basin

CHENG Meng-meng，CHEN Jin
（Yangtze River Scientific Research Institute，Wuhan 430010，China）

The population growth and economic developmentaswell as the ever increasing demand for domestic and production water gave rise to a growing contradiction between water supply and demand.Low efficiency ofwater use and severewater waste have not been effectively controlled.It is imperative to allocatewater fairly and reasonably，improve water use efficiency and alleviate the imbalance ofwater supply and demand.A semi-structural and multiobjective fuzzy optimal selection model is established and is taken to allocate water resources among all regions in Ganjiang River Basin.The approach is aimed at providing a viablemethod for the water allocation in the basin.

semi-structural and multi-objective fuzzy optimal selection；water allocation；Ganjiang River Basin

TV213

A

1001－5485（2011）12－0010－05

2011-10-18

水利部公益性行业专项经费项目（201001005）

程孟孟（1987-），女，河南许昌人，硕士研究生，主要从事水文水资源研究，（电话）15071147692（电子信箱）chengmengmeng271671＠163.com。