软弱路基土体三轴蠕变试验及蠕变模型研究
徐进,张家生,赵同顺,黄林冲
(1. 中南大学 土木工程学院,湖南 长沙,410075;2. 中国矿业大学 土木建筑学院,北京,100083;3. 中山大学 工学院,广东 广州,510275)
蠕变模型可以分为线性蠕变模型和非线性蠕变模型,许多学者对非线性模型进行了研究,如:韦立德等[1]根据岩石黏聚力在蠕变中的作用提出了一个新的SO非线性元件模型,建立了新的一维黏弹塑性本构模型;金丰年等[2]基于试验结果,结合传统线性黏弹性模型的分析,提出了非线性黏弹性模型;邓荣贵等[3]根据岩石加速蠕变阶段的力学特性,提出了一种非牛顿流体黏滞阻尼元件,将该阻尼元件与描述岩石减速蠕变和等速蠕变特性的传统模型结合,构成了新的综合蠕变力学模型;王来贵等[4]以改进的西原正夫模型为基础,利用岩石全程应力-应变曲线与蠕变方程中参数的对应关系,建立了参数非线性蠕变模型;徐卫亚等[5]将提出的非线性黏塑性体与五元件线性黏弹性模型串联,建立一个新的岩石非线性黏弹塑性蠕变模型(河海模型)。在软土非线性蠕变模型研究中,Leoni等[6-7]提出了各向异性的蠕变模型,蠕变模型和参数的识别是蠕变学中的两大研究主题,夏才初等[8]根据岩石在不同应力水平下的加卸载蠕变试验曲线,对元件组合模型进行识别和确定其参数。孙钧[9]对此也在早期有过研究,采用上述方法建立了不同的蠕变本构模型并确定了模型参数。此外,Cogan等[10-11]针对不同类型的土开展了大量的蠕变试验研究,Mukai等[12]改进了蠕变测试仪。在此,本文作者采用GDS三轴试验仪对软土地基处理后的路基土体进行三轴蠕变试验,研究路基土体蠕变工程性质,通过试验确定蠕变模型的参数。
1 三轴蠕变试验
1.1 蠕变试验设计
本工程位于广州市大学城,属于城市主干道级别道路(Ⅰ级),路面宽度为24 m。场地处于珠江入海口的低丘陵地带,依据工程勘察报告,地层条件从上到下依次为:耕土、淤泥质软土、粉质黏土、黏土和基岩。其中对k8+000~k10+300 km段软土路基进行挤密砂桩地基处理,主要加固粉质黏土和淤泥质土。为了研究路基处理后的地基蠕变变形及考虑蠕变的路基沉降计算,对地基处理后的路基土体进行三轴蠕变试验研究。结合实际情况,对粉质黏土和淤泥质黏土进行试验,土体物理力学性能见表1。
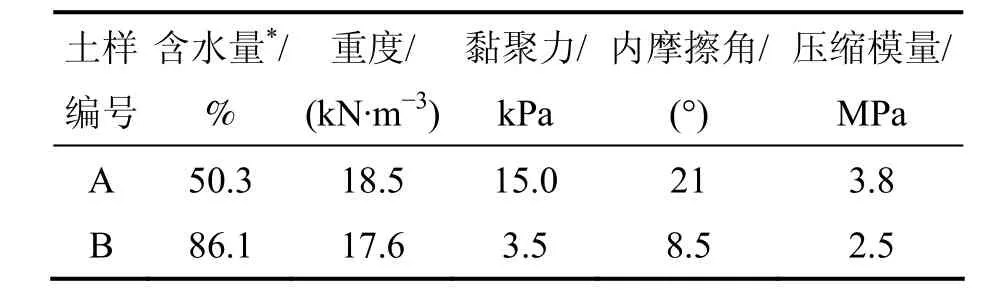
表1 土样的物理力学性能Table 1 Physical and mechanical parameters of soil
试样直径×高为39.1 mm×50.0 mm。为了模拟现场的砂桩地基处理效果,土样按与地基处理面积相等置换率插入微小砂桩。微小砂桩实施方法为:先在土样中打孔,然后灌入中粗砂填满土样中的小孔,最后适当夯实,试验土样见图1。
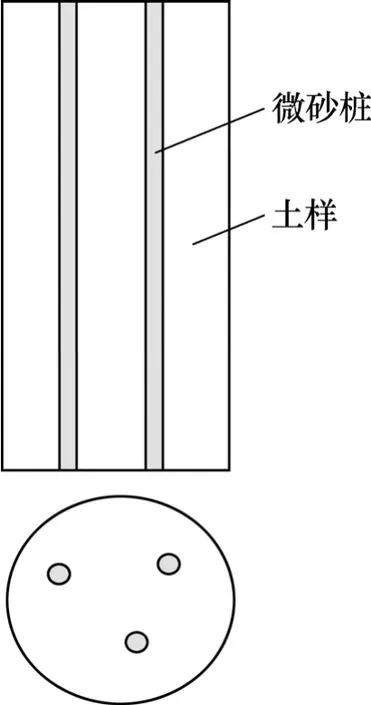
图1 地基土试验土样Fig.1 Rheological test soil samples of foundation
每组土样进行3种不同围压的6个应力水平试验,土样的试验方案见表2。蠕变试验在GDS三轴试验仪上进行,采用分级加载方式。
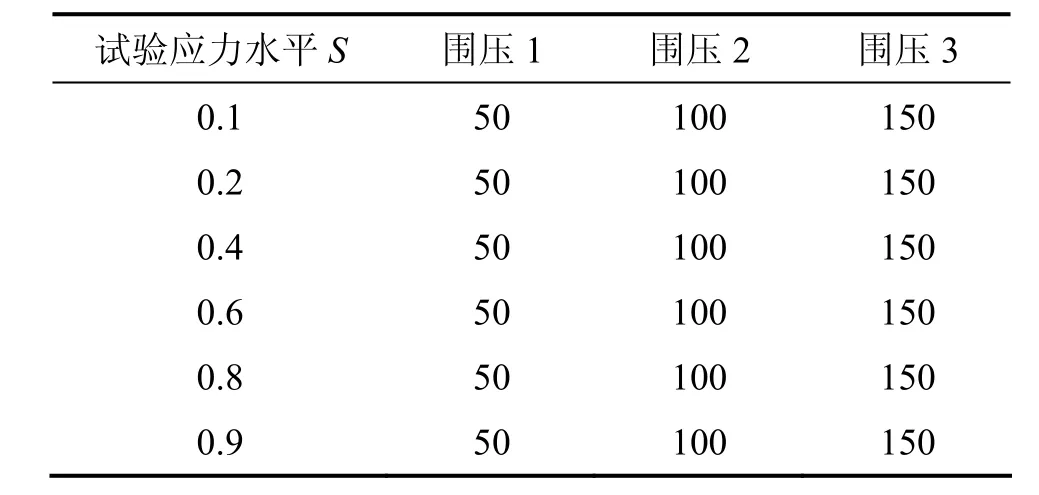
表2 土样蠕变试验方案Table 2 Rheological test plan of samples kPa
1.2 蠕变试验分析
路基土体蠕变试验曲线见图 2~7。其中:围压为50 kPa时蠕变曲线见图2~3;围压为100 kPa时土体蠕变曲线见图4~5;围压为150 kPa时,路基土体蠕变曲线见图6~7。
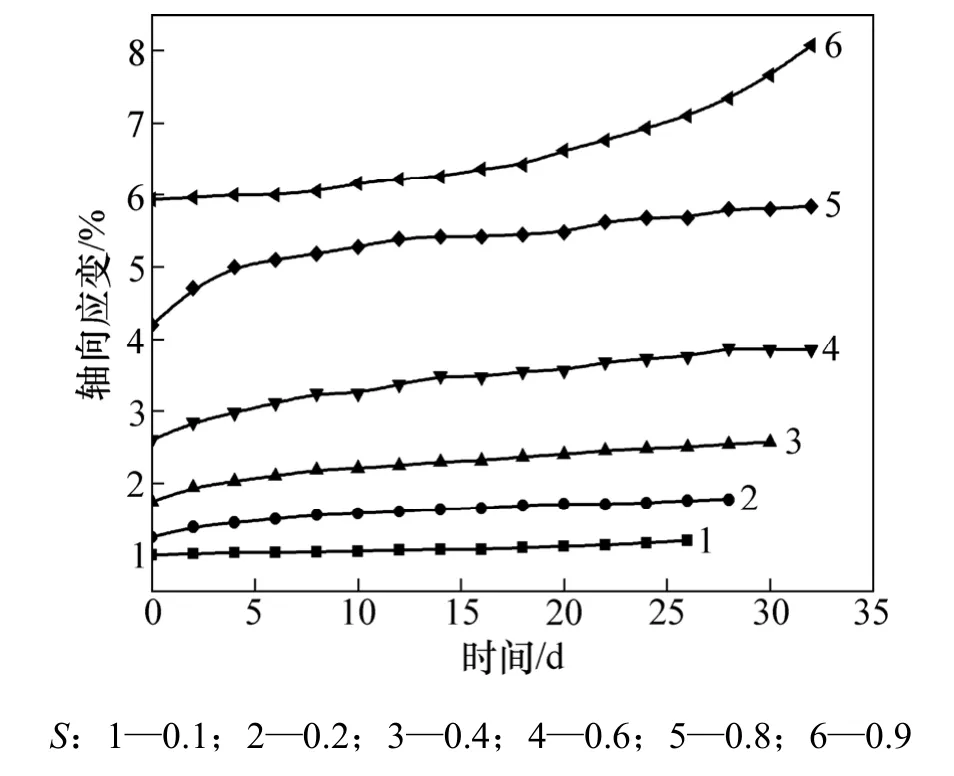
图2 50 kPa围压下A-1 蠕变试验曲线Fig.2 Creep curves of A-1 under 50 kPa confining pressure
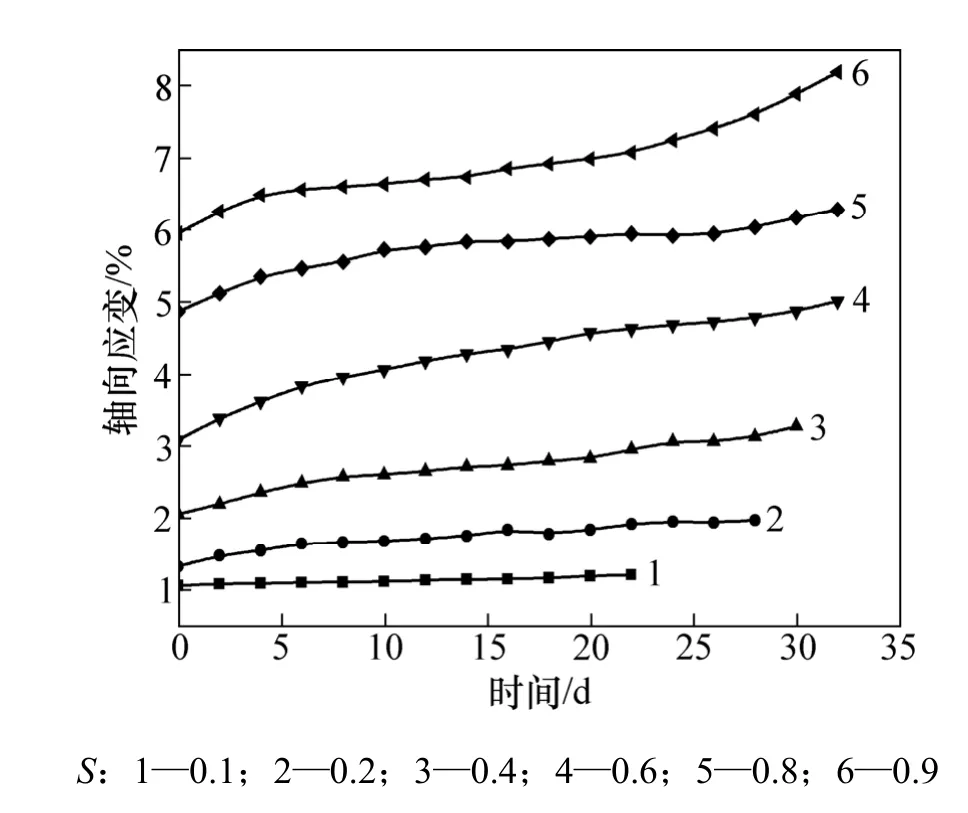
图3 50 kPa围压下B-1 蠕变试验曲线Fig.3 Creep curves of B-1 under 50 kPa confining pressure
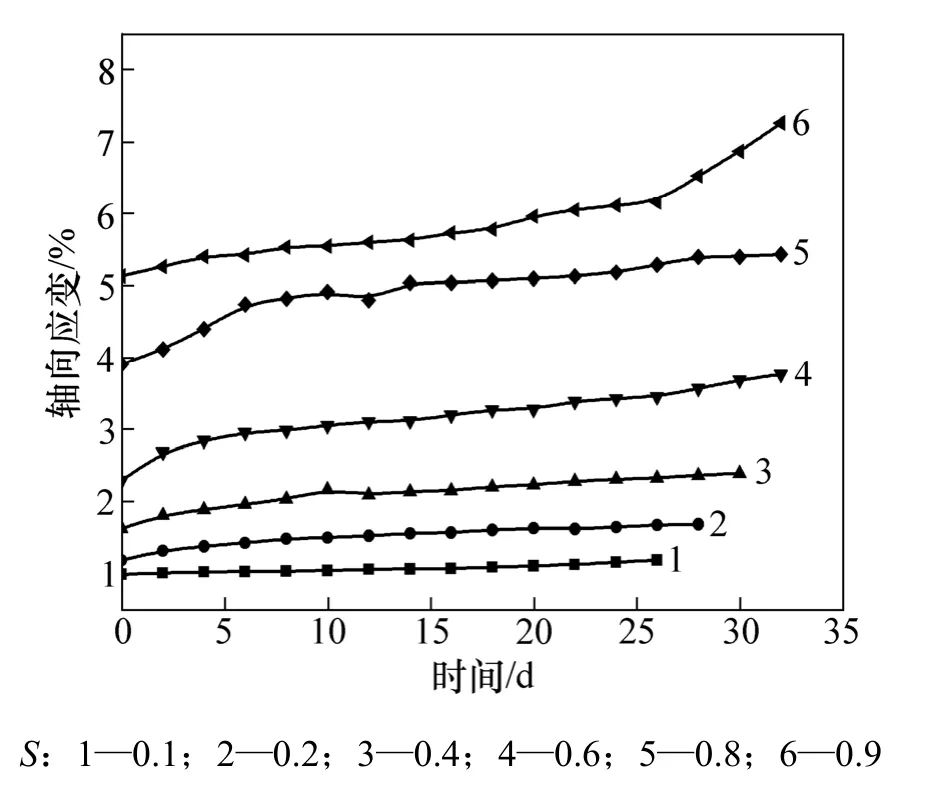
图4 100 kPa围压下A-2蠕变试验曲线Fig.4 Creep curves of A-2 under 100 kPa confining pressure
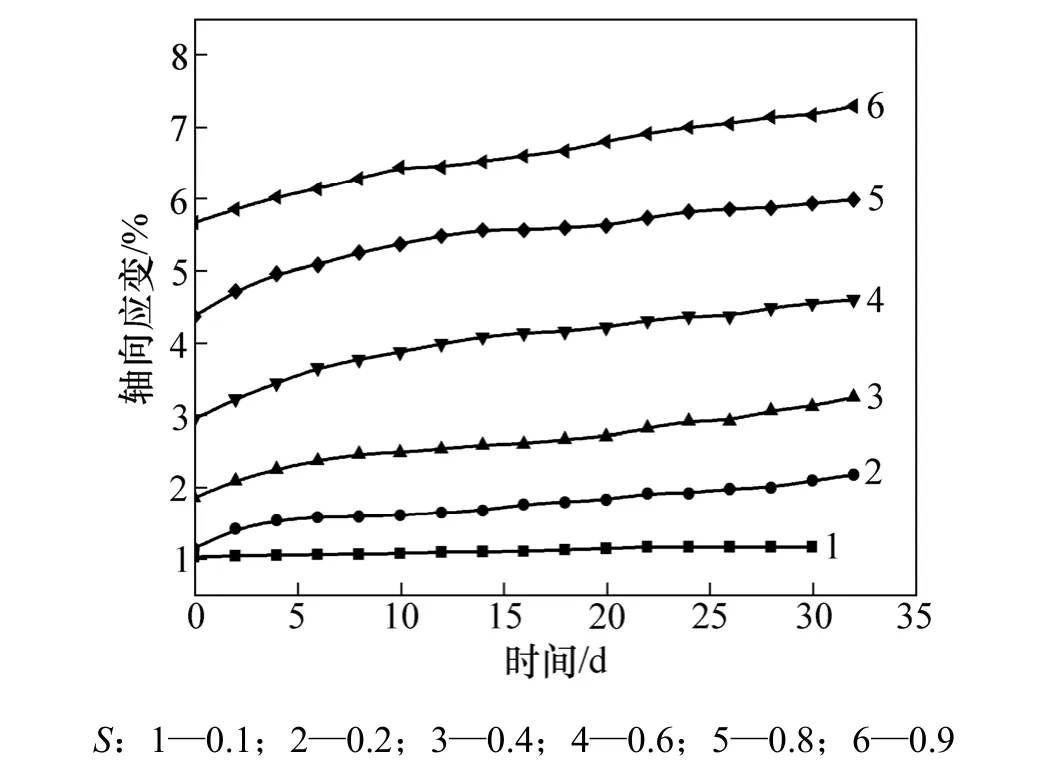
图5 100 kPa围压下 B-2 蠕变试验曲线Fig.5 Creep curves of B-2 under 100 kPa confining pressure
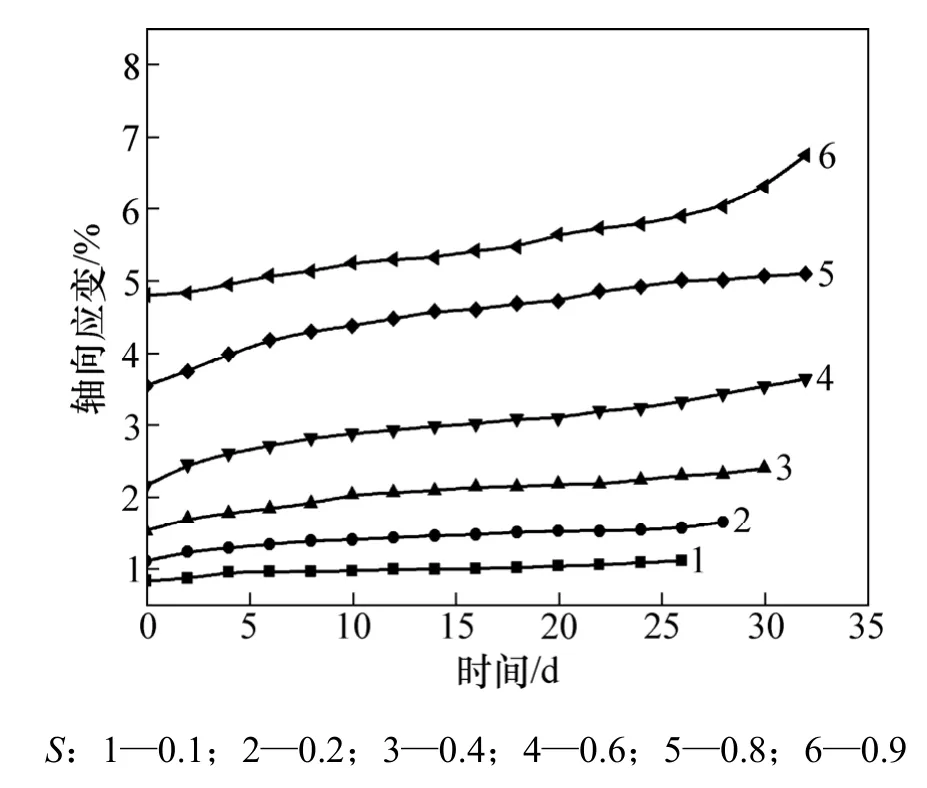
图6 150 kPa围压下A-3蠕变试验曲线Fig.6 Creep curves of A-3 under 150 kPa confining pressure
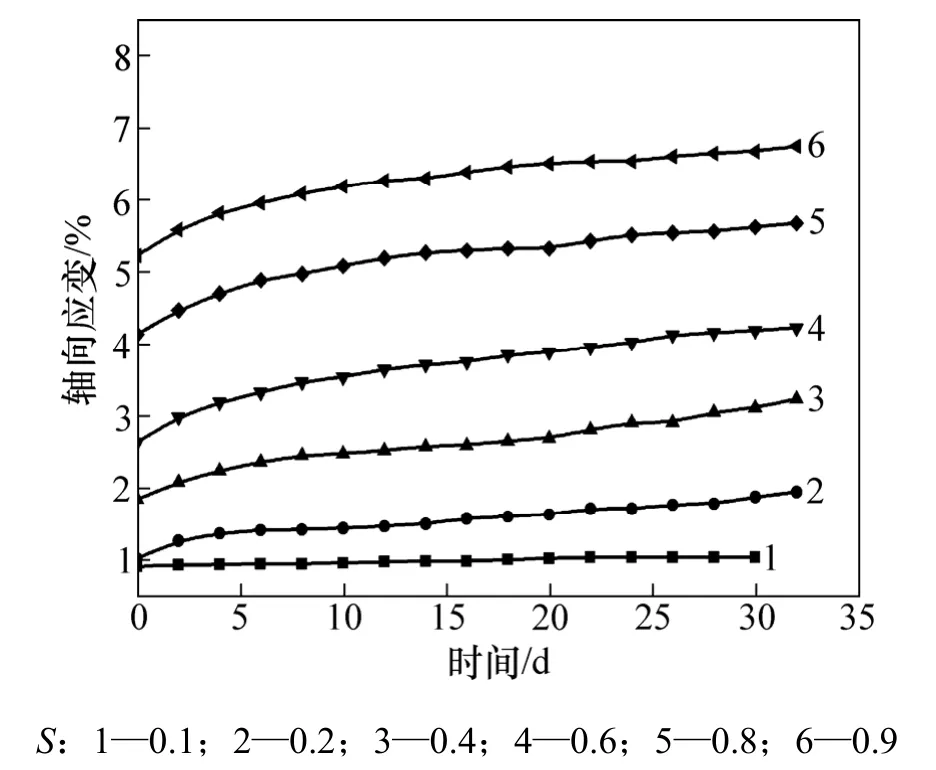
图7 150 kPa围压下B-3 蠕变试验曲线Fig.7 Creep curves of B-3 under 150 kPa confining pressure
从图2~7可见:在较低的应力水平下(S≤0.4),轴的应变曲线表现出相同的趋势,具有初始应变,前期蠕变发展快速,后期蠕变逐步减缓并呈稳定增长趋势,即只有衰减阶段和稳定阶段,并且趋向平缓,蠕变变形收敛,土体表现出明显的线性黏弹性;在中等应力水平 S下(0.4<S≤0.6),轴向应变曲线虽然也有类似的规律,但是,蠕变变形量增大,具有蠕变速率衰减阶段和蠕变速率稳定阶段,蠕变变形没有明显的收敛趋势,曲线斜率稳定,部分曲线表现出黏塑性特征;在较高的应力水平下(S>0.6),轴向应变曲线与前面的蠕变曲线差别较大,出现了加速蠕变阶段,表现为非线性黏塑性变形特征。
2 蠕变模型分析
2.1 蠕变模型
依据路基土体蠕变试验结果,提出1个基于双曲线型的非线性黏性元件模型,并将其与塑性元件并联,模型力学结构如图8所示。
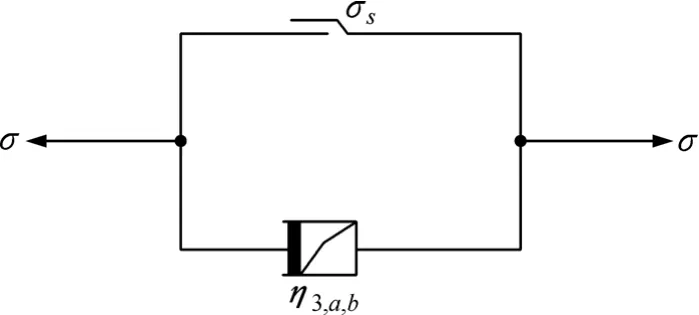
图8 非线性黏塑性体Fig.8 Non-linear visco-plastic body
在恒定的应力σ0下蠕变方程为:
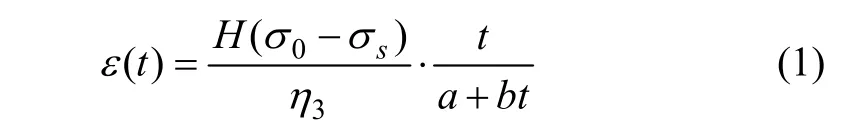
式中:a和b为蠕变参数,由试验确定;H(σ0-σs)为对应的某个屈服准则,
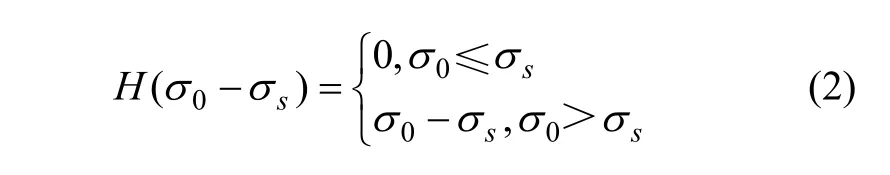
把非线性黏塑性模型与 Burgers模型串联建立 1个非线性黏弹塑性蠕变模型(EPRM),就能描述路基土体整个蠕变变形,其力学模型如图9所示。
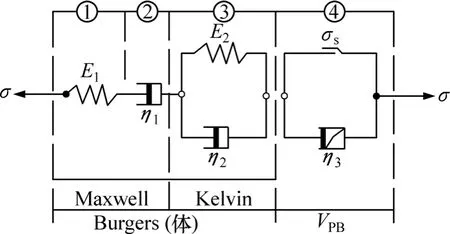
图9 EPRM蠕变模型Fig.9 EPRM rheological model
该模型有①,②,③和④4个部分组成。当土体屈服前,σ<σs,模型就只有①、②和③部分(见图 9)作用,此时,模型(EPRM)退化为Burgers模型。
当土体屈服时,σ≥σs,模型有①,②,③和④部分作用,此时,模型(EPRM)各个元件的状态为:
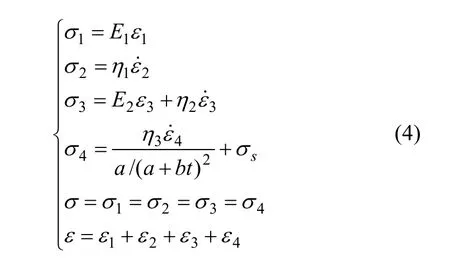
同样,令微分算子 D =∂/∂t ,得到:
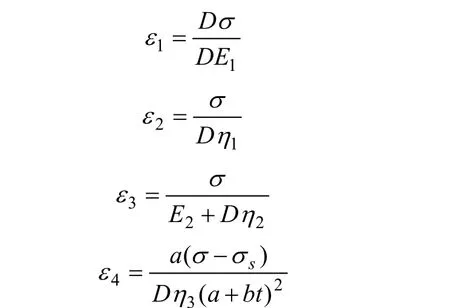
最后,由 ε=ε1+ε2+ε3+ε4得到 EPRM 蠕变模型的本构方程为:
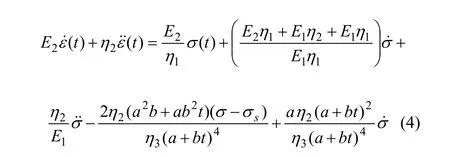
式中:ε为总应变;σ为总应力;σs为屈服应力;ε1,ε2,ε3和 ε4为各个部分对应的应变;σ1,σ2,σ3和 σ4为各个部分对应的应力;E1和E2为弹性参数;η1,η2和η3为黏性参数。
2.2 蠕变特性分析
在t=0时,EPRM模型各个元件处于自然状态,满足如下关系:
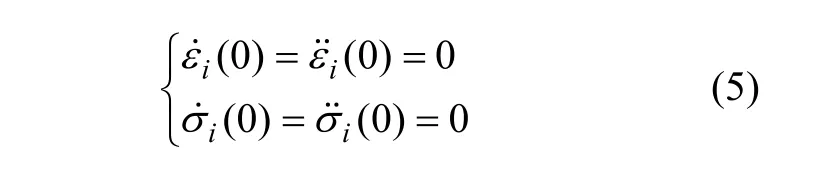
其中:i=1,2,3,4。在恒定应力σ0下,该非线性弹塑性蠕变模型(EPRM)的蠕变方程分为2种情况。
当σ0<σs时,土体未进入屈服状态,EPRM退化为Burgers模型。引入Heaviside单位函数和Dirac脉冲函数 δ(t):
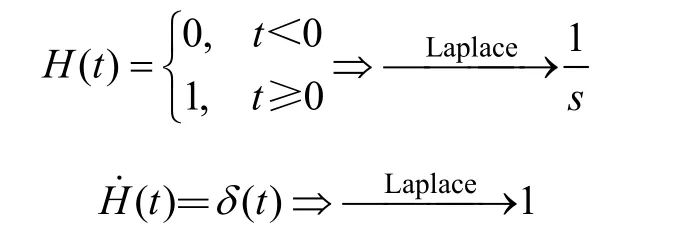
式中:s为Laplace相函数的自变量。得σ=σ0H(t)代入式(3)并进行Laplace变换,得到:
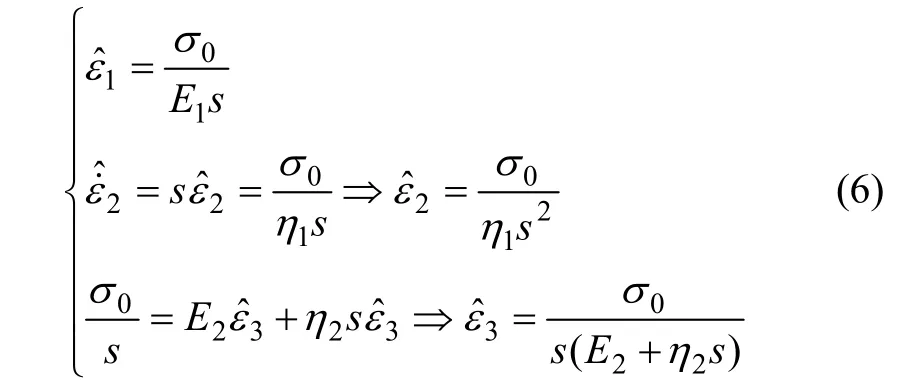
最后得到:
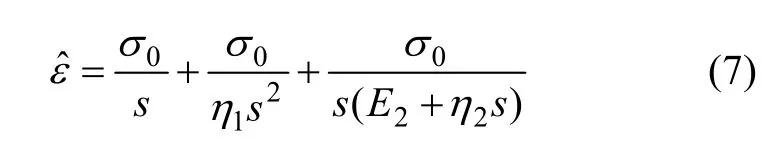
对式(7)进行Laplace逆变换,即得EPRM蠕变方程:
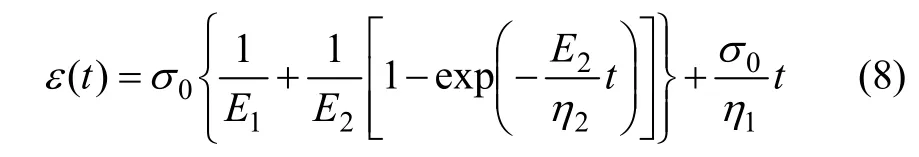
此时,蠕变柔度J(t)表达时为:
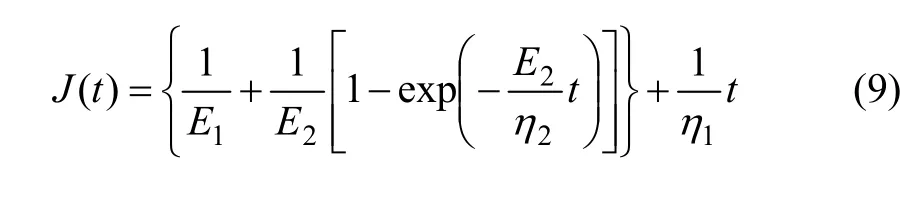
对蠕变方程(15)式求一阶导数和二阶导数得:
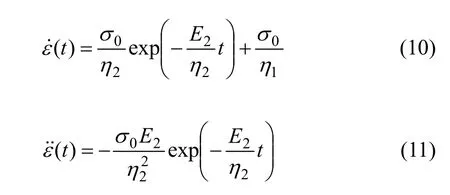
(2) 当 σ0≥σs时,土体进入屈服状态,EPRM 为非线性黏弹塑性蠕变模型,把σ=σ0H(t)代入式(3)并进行Laplace变换得到:
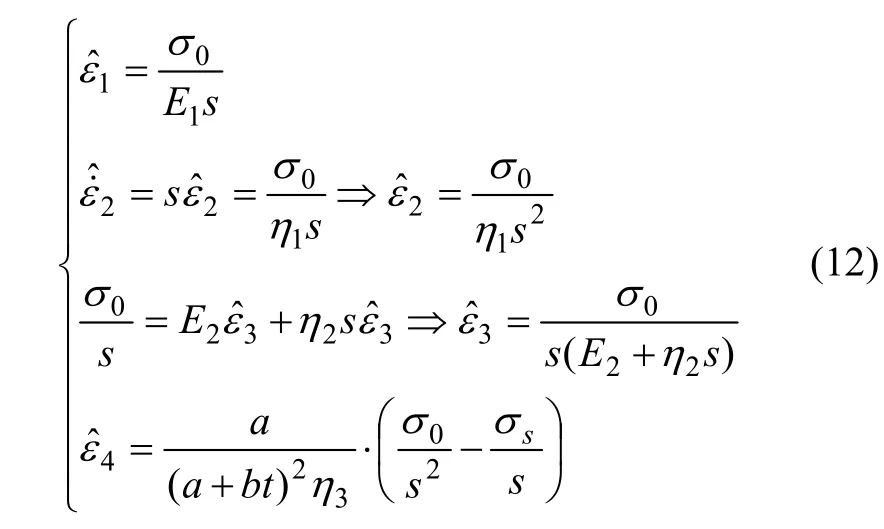
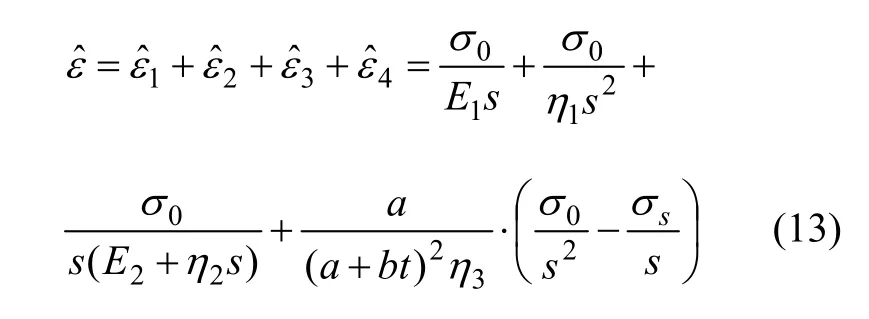
对式(13)进行 Laplace逆变换则得到了蠕变方程表达式:
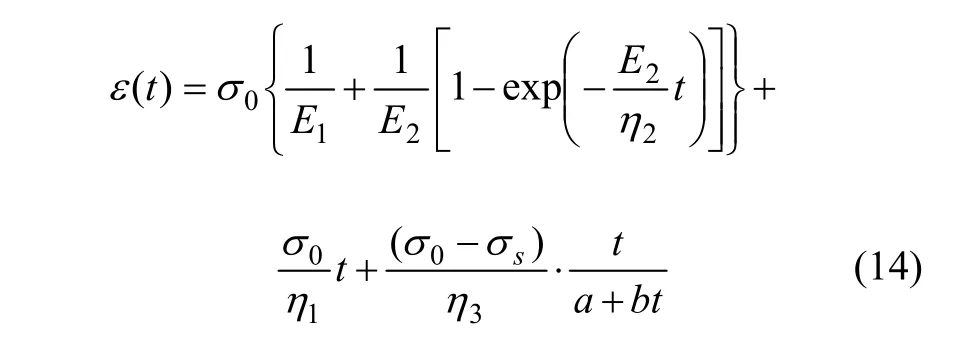
对(14)式取一阶和二阶导数得:
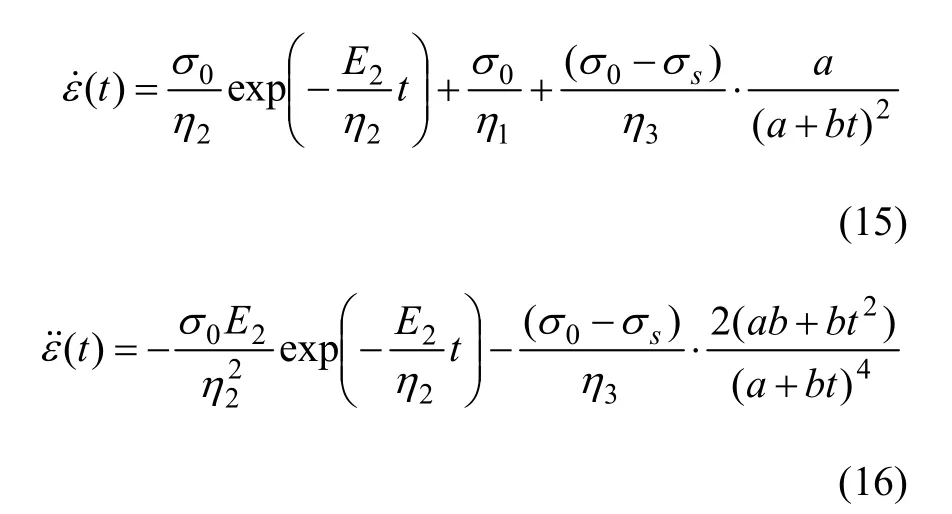
分析式(15)和(16)得知:当 a>0 时,ε˙(t)>0 。但是,(t)的符号不能确定,(t)的符号可能大于 0、等于0或者小于0,正好反映了蠕变曲线的3个阶段:衰减蠕变、稳态蠕变和加速蠕变阶段,见图10。
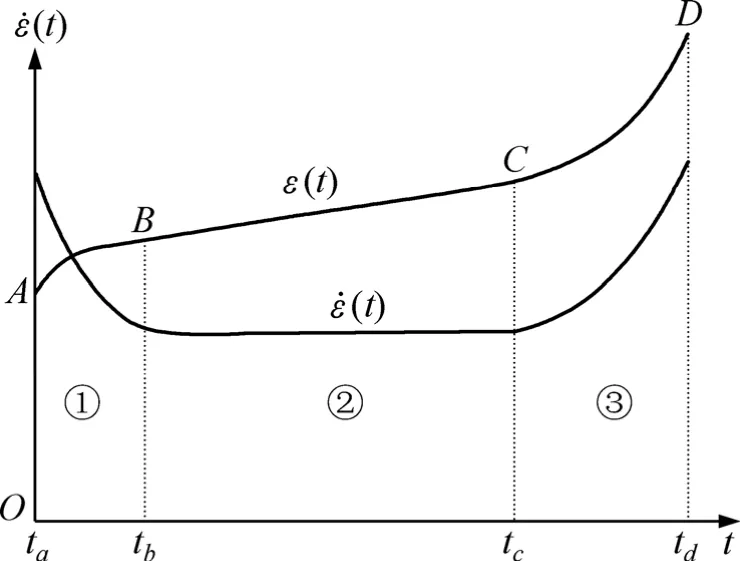
图10 EPRM蠕变模型蠕变曲线Fig.10 Creep curve of EPRM rheological model
3 蠕变模型参数确定
蠕变本构模型总共有6个参数有待识别,采用改进的最小二乘拟合算法[13-14],依据蠕变试验曲线进行拟合得到蠕变本构模型参数,见表3。
依据力学理论将如下的符号进行对调,即可拓展三维状态下 (EPRM)的蠕变方程为:
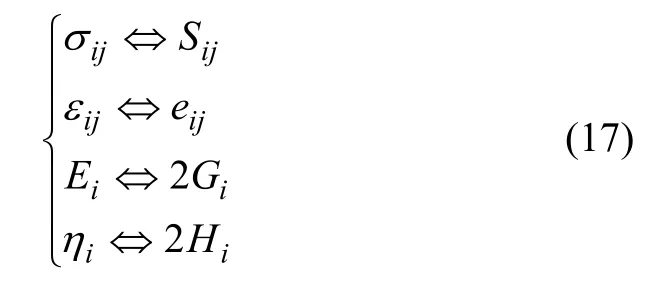
i=1,2,3,…。当 σ0<σs时:
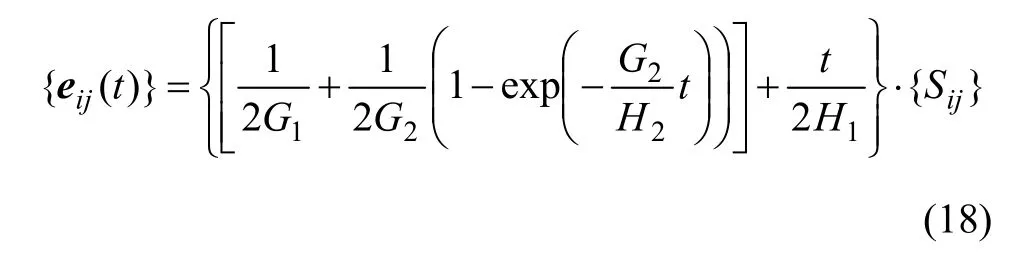
当 σ0≥σs时:
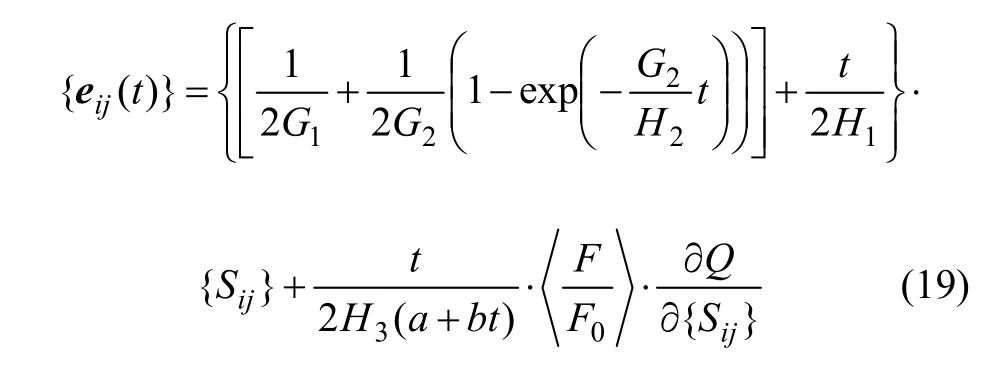
三维蠕变模型EPRM的参数见表4。
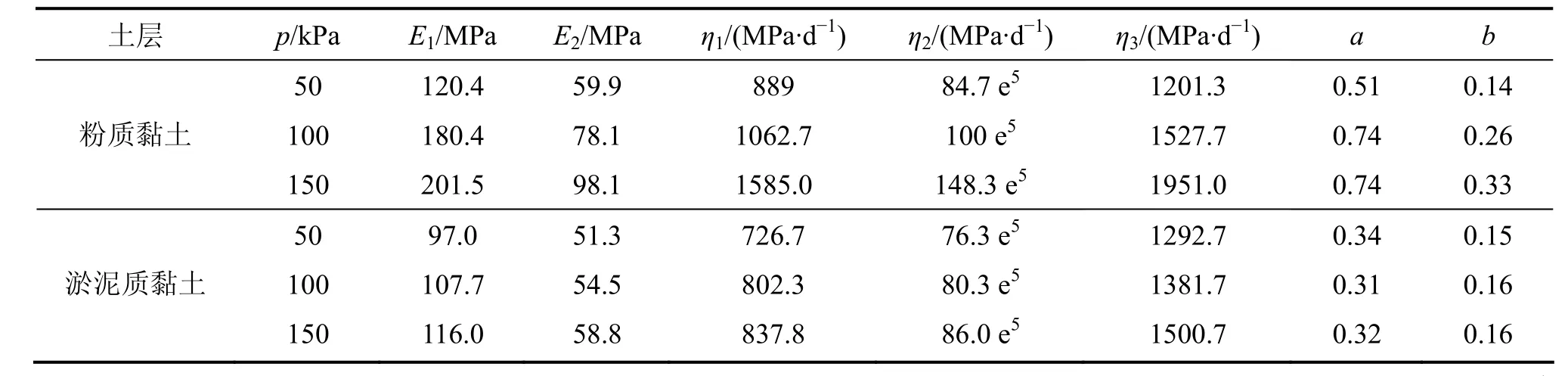
表3 路基土体蠕变模型参数Table 3 Rheological model parameters of embankment foundation soil
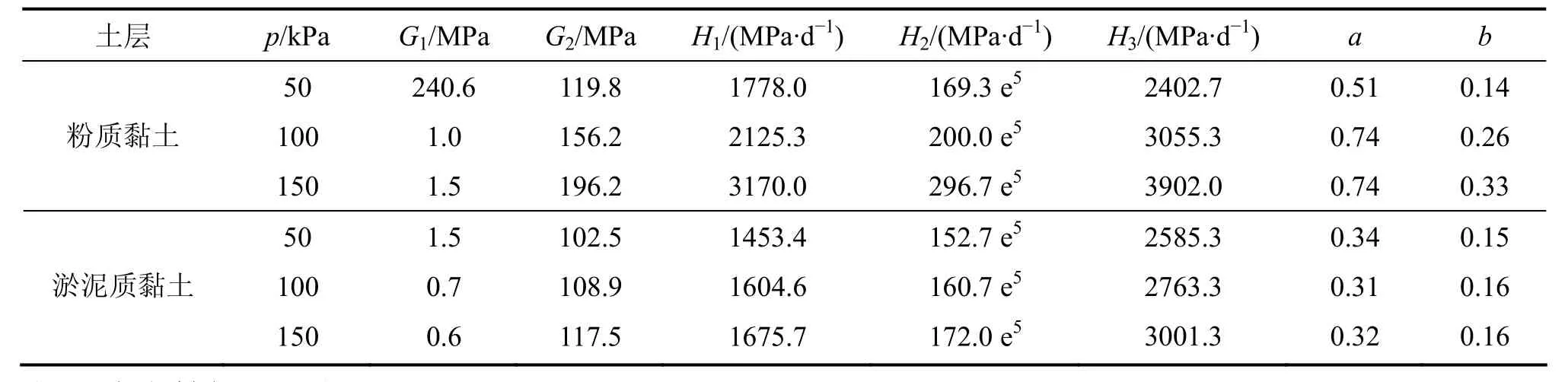
表4 路基土体三维蠕变模型参数值Table 4 Rheological 3D model parameters of embankment foundation soil
4 结论
(1) 应力水平 S是影响路基土体土蠕变的重要因素, S=0.6是1个临界值。试验表明:当S<0.6时,路基土体表现出线性黏弹性蠕变特征;当0.6<S时,表现出非线性黏弹塑性蠕变特征。
(2) 提出了一个基于双曲线函数核的黏性蠕变元件,并与塑性元件并联建立黏塑性元件模型(PRM),描述了路基土体的非线性黏塑性蠕变特征和加速蠕变阶段。
(3) 将PRM与Burges元件模型串联建立非线性黏弹塑性蠕变本构模型(EPRM),将模型扩展到三维状态,通过试验确定了模型参数。该模型为考虑流变的路基沉降计算提供了工具。
[1] 韦立德, 徐卫亚, 朱珍德, 等. 岩石黏弹塑性模型研究[J]. 岩土力学, 2002, 23(5): 583-586.WEI Li-de, XU Wei-ya, ZHU Zhen-de, et al. Study on constitutive model of Viscoelastoplastic rock[J]. Rock and Soil Mechanics, 2002, 23(5): 583-586.
[2] 金丰年, 范华林. 岩石的非线性蠕变损伤模型及其应用研究[J]. 解放军大学学报, 2000, 1(3): l-5.JIN Feng-nian, FAN Hua-lin. Study on nonlinear rheology damage property of rock[J]. Journal of PLA University of Science and Technology, 2000, 1(3): 1-5.
[3] 邓荣贵, 朱德培, 张倬元, 等. 一种新的岩石蠕变模型[J]. 岩石力学与工程学报, 2001, 20(6): 780-784.DENG Run-gui, ZHOU De-pei, ZHANG Zhuo-yuan, et al. A new rheological model for rocks[J]. Chinese Journal of Rock Mechanics and Engineering, 2001, 20(6): 780-784.
[4] 王来贵, 何峰, 刘向峰, 等. 岩石试件非线性蠕变模型及其稳定性分析[J]. 岩石力学与工程学报, 2004, 23(10): 1640-1642.WANG Lai-gui, HE Feng, LIU Xiang-feng, et a1. Nonlinear creep model and stability analysis of rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(10): 1640-1642.
[5] 徐卫亚, 杨圣奇, 褚卫江. 岩石非线性黏弹塑性蠕变模型及其应用[J]. 岩石力学与工程学报, 2006, 25(3): 430-447.XU Wei-ya, YANG Sheng-qi, CHU Wei-jiang. Nonlinear viscoelasto-plastic rheological of rock and its engineering application[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(3): 430-447.
[6] Leoni M, Karstunen M, Vermeer P A. Anisotropic creep model for soft soils[J]. Geotechnique, 2008, 58(3): 215-226.
[7] 孙钧. 岩土材料蠕变模型及其工程应用[M]. 北京: 建筑工业出版社, 1999: 10-28.SUN Jun. Rheology of geomaterial and its engineering application[M]. Beijing: China Architecture and Building Press,1999: 10-28.
[8] 夏才初, 孙钧. 蠕变试验中蠕变模型辨识及参数确定[J]. 同济大学学报, 1996, 24(5): 498-503.XIA Cai-chu, SUN Jun. Distinction of rheological model and determination of parameters on creep tests[J]. Journal of Tongji University, 1996, 24(5): 498-503.
[9] Cogan J. Triaxial creep tests of opohonga limestone and ophir shale[J].International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1976, 13(1): 1-10.
[10] di Prisco C, Imposimato S, Vardoulakis I. Mechanical modelling of drained creep triaxial tests on loose sand[J]. Geotechnique,2000, 50(1): 73-82.
[11] Wijeweera H, Joshi R C. Creep behavior of fine-grained frozen soils[J]. Canadian Geotechnical Journal, 1991, 28(4): 489-502.
[12] Mukai S, Komatsu Y, Ueda D, et al. Development of triaxial tension creep test machine[J]. Journal of the Society of Materials Science, 1997, 46(12): 1374-1380.
[13] 许宏发, 陈新万. 多项式回归间接求解岩石蠕变力学参数德方法[J]. 有色金属, 1994, 46(4): 19-22.XU Hong-fa, CHEN Xin-wan. Method to find indirectly solution of rock rheology’s parameters with polynomial regression[J].Nonferrous Metals, 1994, 46(4): 19-22.
[14] 李青麒. 软岩蠕变参数的曲线拟合计算方法[J]. 岩石力学与工程学报, 1998, 17(5): 559-564.LI Qing-qi. Curve fitting method for creep parameter of soft rock[J]. Chinese Journal of Rock Mechanics and Engineering,1998, 17(5): 559-564.

