基于小波分析和神经网络的网络流量预测

李小龙，杨文考

（北京交通大学电子信息工程学院，北京100044）

随着科学技术的飞速发展，网络的使用越来越普遍，它不仅成为人与人沟通的桥梁，也是大家共享资源的良好平台。由于网络带宽的增加以及各种互联网服务的出现，网络上承载的业务量急剧增加，加强网络管理成为一个亟待解决的问题。网络流量的精确预测对于提高网络的服务效率和质量以及网络安全有着非常重要的意义。对网络流量的预测成为流量工程、拥塞控制和网络管理的核心问题。传统的网络流量预测方法已不能完全满足当前巨大数据量的预测要求。

本文选用小波分析与神经网络结合的算法，结合小波分析与神经网络对处理实际问题的各种优点，进行实时网络流量预测。仿真结果表明，该方法具有良好的函数逼近能力，预测能力强大，较传统方法具有更强的容错性和鲁棒性，同时具有较强的自适应能力和抗干扰能力。

1 基本理论

1.1 小波变换简介

小波分析是时间频率分析的一种信号变换方法。传统的信号分析是建立在傅立叶变换基础上的，但傅立叶变换是一种只有频域的分析方法，它反映的是一个信号全部时间内的整体频域特性，不能提供任何局部时间段上的频率信息。这些局部时频域信息恰恰是非平稳信号最根本和最关键的信息。小波变换继承和发展了短时傅立叶变换（STFT）的局部化思想，同时克服了窗口大小不随频率变化、缺乏离散正交基的缺点，通过伸缩和平稳等运算功能对函数或信号进行尺度的细化分析，解决了傅立叶变换不能解决的许多困难问题，是一种更为理想的进行信号处理的数学工具。

本文采用Daubechies（简写为dbN，其中N是小波的阶数）小波对流量序列进行小波分解与重构。小波函数f(t)和尺度函数φ(t)中的支撑区为2N-1，小波函数的消失矩为N。除N=1外，dbN不具有对称性（即非线性相位）。Daubechies小波具有以下特点：

（1）在时域上，dbN是有限支撑的，即小波函数长度有限，且N值越大，小波函数的长度就越长；

（2）在频域上小波函数在ω=0频率点处有N阶零点；

（3）小波函数f(t)和它的整数位移正交归一；

（4）小波函数f(t)可以由尺度函数φ(t)求出。

本文选取分解水平为4的Daubechies小波对信号进行多分辨率分析。

1.2 小波神经网络

基于误差反向传播算法的人工神经网络（BP神经网络）包括输入层、隐含层和输出层，其基本原理是利用输出后的误差来估计输出层的直接前导层的误差，再利用这个误差估计更前一层的误差，如此一层一层的反传下去，就可获得了所有其他各层的误差估计。

神经网络在外界输入样本的刺激下不断改变网络的连接权值，以使网络的输出不断接近期望的输出，在学习过程中，网络中各神经元的连续权变换要依据一定的调整规则，即通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小。

小波神经网络的基元和整个结构是依据小波分析理论确定的，可以避免BP神经网络等结构设计上的盲目性。隐含层选取的神经元激励函数为Morlet小波：

隐含层输出为：

小波神经网络不同于其他小波网络，训练时，在权值和阈值的修正算法中需加入动量项，利用前一步得到的修正值来平滑学习路径，避免陷入局部极小值，加速学习速度。为了避免在逐个样本训练时引起权值和阈值修正所发生的振荡，需采用成批训练方法。对网络的输出也并非简单的加权求和，而是先对网络隐含层小波结点的输出加权求和，再经Sigmoid函数变换后，得到最终的网络输出，该方法有利于处理分类问题，同时减少训练过程中发散的可能性。同时通过调整网络的各项参数，使得误差函数达到最小值。

2 模型预测的选取

按照预测方法的不同，预测模型可分为计量模型、神经网络模型、非线性系统理论模型等。每一种预测模型均具有其自身的优缺点，根据对网络流量的非线性与各时段较大的需求差异性的分析，准确的网络流量预测模型不能依靠单一的模型或方法，应当根据实际情况在预测过程中选用最适合的模型或是组合模型，根据预测的效果对模型进行判断和评价，以便继续优化模型。

本文中采用神经网络与非线性预测的组合模型，即将神经网络与小波分析结合，利用它们各自的优点，得到更强的函数逼近能力，增加了预测的精度以及计算速度。文中所采用的预测模型结构图如图1。

图1 基于神经网络和小波分析的网络流量预测模型

3 实验分析与结果

本文采用Matlab实现对原始数据的小波分析及神经网络测试功能。网络数据流采用北京交通大学某上网账号4月～5月中连续60天的网络流量数据，共有60个数据，选取前56个数据作为输入构建模型，后4个数据作为预测值的比较对象，检测预测效果。如图2。

给定p（p=1, 2, …, P）组输入输出样本，预测目标误差函数

图2 某网络账户连续60天网络流量

对提取的流量数据采用Daubechies4小波进行多分辨率分析，从而得到分解后的高频信号序列和低频信号序列，如图3。

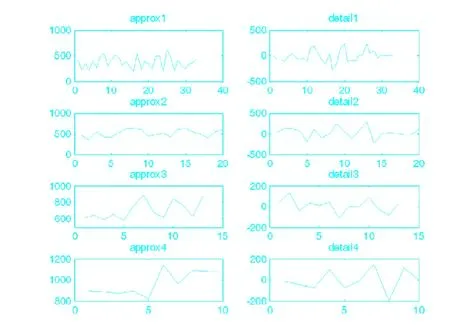
图3 小波分解结果

从图3中可以看出，低频信号序列反映了网络流序列的总体特征，信号曲线更光滑，高频信号序列明显提取和放大了原始信号的局部特征。对低频部分和高频部分分别进行小波分析和神经元网络预测，为避免神经网络输入维数过多导致训练耗时长且预测精度低，取输入维数为6，小波函数的隐层单元个数不大于10，各个子网的输出结果合成后为预测结果，如图4。应用此方法所得到的全局误差E=9.1036。预测结果如表1显示，选用该模型进行短时网络流量预测对比经典神经网络进行预测的性能有所提升。

表1 经典神经网络与小波神经网络实验结果误差对比

图4 实际流量与预测流量对比

4 结束语

本文利用小波网络与神经网络的组合模型对网络流量进行预测。充分利用了小波分析和神经网络的优势，通过对流量信号的高频分量和低频分量分析，采用神经网络进行多次训练，得到的仿真效果较单一模型有很大的提高。实验结果表明，这种模型对网络流量的预测准确率高，误差较小。

[1] C.L.Wu,K.W.Chau*,Y.S.Li.Methods to improve neuralnetwork performance in daily flows prediction[J] .Journal of Hydrology,(2009), 372:80.

[2] Eleni I.Vlahogianni,Matthew G.Karlaftis*,John C.Golias.Optimized and meta-optimized neural networks for short-term traffic flow prediction:A genetic approach. [J] .TRANSPORTATION RESEARCH PART C 13,(2005):211.

[3] 王兆霞，孙雨耕，陈增强等. 基于模糊神经网络的网络业务量预测研究[J] . 通信学报，2005，3（3）：136.

[4] 彭玉华. 小波变换与工程应用[M] . 北京：科学出版社，2000.

[5] 张良均. 神经网络实用教程[M] . 北京：机械工业出版社，2008.

[6] 胡俊，胡玉清，肖中卿. 基于小波变换的网络流量预测模型[J] . 计算机工程，2008，19：112.

[7] 马社祥，刘贵忠，曾召华. 基于小波的非平稳时间序列分析与预测方法[J] . 系统工程学报，2000（4）.

[8] 高光勇，吴维勇，邓安远. 基于小波分析和神经网络的网络流量预测[J] . 通信技术，2008，41（4）：93-95.

[9] 胡昌华. 基于MATLAB的系统分析与设计—小波分析[M] .西安：电子科技大学出版社，2001.