一种新型阈值决策的小波去噪方法

邱爱中

（郑州师范学院物理系，河南 郑州 4500443）

0 引言

在通信中信号去噪有着重要的作用。Donoho提出的统一阈值降噪法是针对多维独立正态变量联合分布的[1-2]。在利用阈值去噪方面，主要有硬阈值函数法和软阈值函数法。硬阈值法可以很好地保留信号边沿的局部特征，但会出现振铃、伪 Gibbs效应等失真，而软阈值函数法处理相对要平滑，但可能造成边沿模糊等失真现象[3-4]。为了解决以上问题，将一种新型阈值函数引入信号去噪，以期实现更好的去噪效果。

固定阈值会产生过扼杀现象，如果在同一级尺度上都采用同一阈值，在较低尺度上，会去除有用信息，在最大尺度级上，则会留下一部分噪声。为此，采用自适应的阈值算法来有效解决这个问题。

文中提出一种基于改进型阈值函数和自适应阈值的去噪方法，分析了改进型阈值函数的特点，给出了自适应阈值计算的方法。理论和试验均说明，该法能获得比常规的离散小波降噪法更好的效果，且保留了原始信号的细节特征，与传统去噪法相比是一种较好的恢复微弱信号的降噪方法。

1 传统阈值函数

在阈值去噪中，阈值函数体现了对超过和低于阈值的小波系数模的不同处理策略以及不同估计方法。根据小波去噪的数学模型，叠加了高斯白噪声的信号可以表示为：

式中：s（t）为真实的信号，e（t）为方差 σ2的高斯白噪声，服从N(0,σ2)分布，k=1,2,…,N-1,N为信号长度。

基于小波变换的去噪主要分为3个步骤：①选择小波和小波分解的层数，根据 Mallat算法对信号做小波变换得出到N层的各级小波分解的系数。②因为噪声主要集中在小波细节系数中，故对每层的细节系数进行滤波，而对尺度系数不做处理。选择软阈值或者硬阈值函数，对小波系数进行收缩处理。③根据第N层的低频系数和第一层到第N层的经过修改过的高频系数，完成信号的小波重构，得到去噪信号作为真实信号的估计[3]。根据 Donoho提出的阈值算法，对小波系数处理的软阈值函数为：

硬阈值函数为：

噪声标准差σn可以用以下经验公式估计，即：

2 改进的阈值函数

小波阈值降噪中阈值量化和阈值函数决定信号重构的连续性和精度。传统的软阈值函数和硬阈值函数在信号的连续性和重构信号与真实信号的逼近程度方面都有各自的不足。软阈值函数降噪，虽然处理的小波系数整体连续，光滑性也好，可是对于大于阈值的小波系数恒定压缩，自然会损失一些有用的高频信息，影响重构信号的真实；硬阈值算法可以避免软阈值的恒定偏差，然而由于小波系数在T±处是不连续的，给重构信号带来一些附加振荡，使重构信号的光滑性变差。改进的思想是要让小波系数的偏差尽可能小，又要在小波空间连续，具有高阶导数，为此，参考文献[4-5]引入新的阈值处理函数，其表达式为：

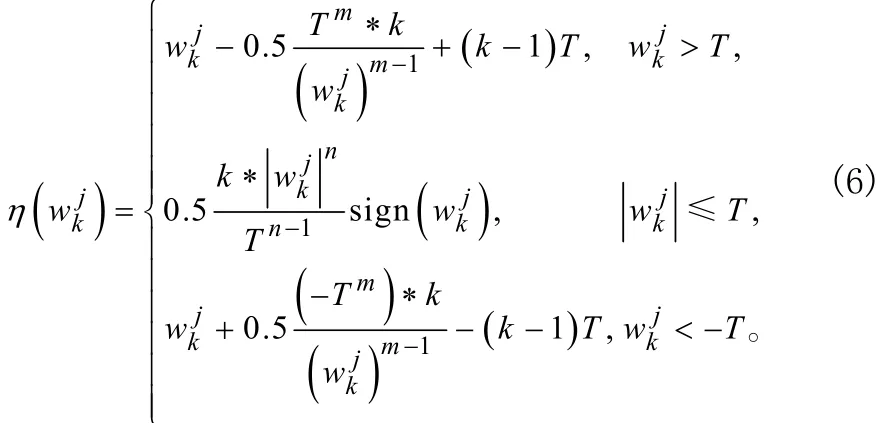
式（6）中，m、n、k为新阈值函数的调解因子，它能较好增强应用的灵活性。m、n决定阈值函数的形式，参数k取值在0到1之间，若k为1，则该阈值函数相当于硬阈值函数；若k为0,相当于软阈值函数。故此，在0到1之间调节参数 k，可以克服硬阈值函数的不连续和软阈值函数在处理小波系数时出现的恒定偏差，同时保留了硬、软阈值原有的优点。该阈值函数具有无穷阶连续导数，为小波阈值的自适应选择提供了基础。

3 自适应阈值计算

其中n为小波系数的个数，由元素iw（i=1,2,…,n）得：

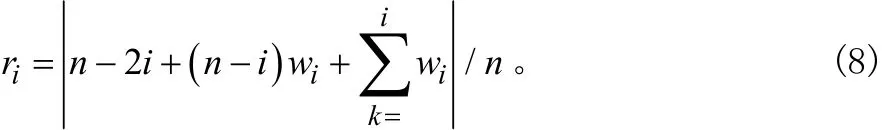
式（8）中ir为引入的风险向量元素，将式（8）多次迭代得出最小的ir，记为0r，与0r对应的iw记为0w，则阈值表达式为：

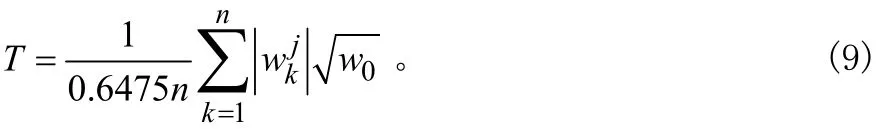
按照该方法将每一级尺度都看作相互独立，计算出一个与之最匹配的阈值来进行降噪，最后再用各个尺度上降噪处理后的系数来重构信号。

4 仿真试验分析

为了验证该算法的降噪效果，利用Matlab构造信号并加入白噪声和有色噪声，生成具有不同信噪比的含噪信号，然后用Daubechies小波作为小波函数，分解级数为4层，采用基于改进型阈值函数和自适应阈值的去噪法进行去噪，再和传统的软阈值函数、硬阈值函数去噪法进行降噪处理比较。以下绘出的信号波形是降噪后最接近原始信号的波形，当在此基础上进一步加大或者减小阈值时，会出现波形失真。由图1～图5可看出基于新阈值函数和自适应阈值的去噪法提高了重构信号的信噪比，较好保留了原始信号的细节特征。

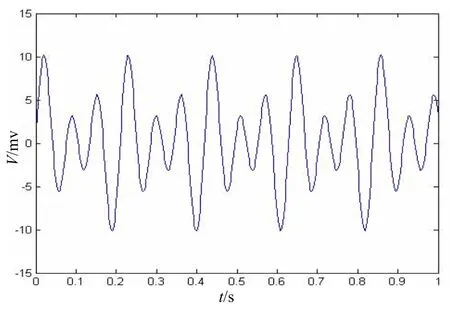
图1 原始信号

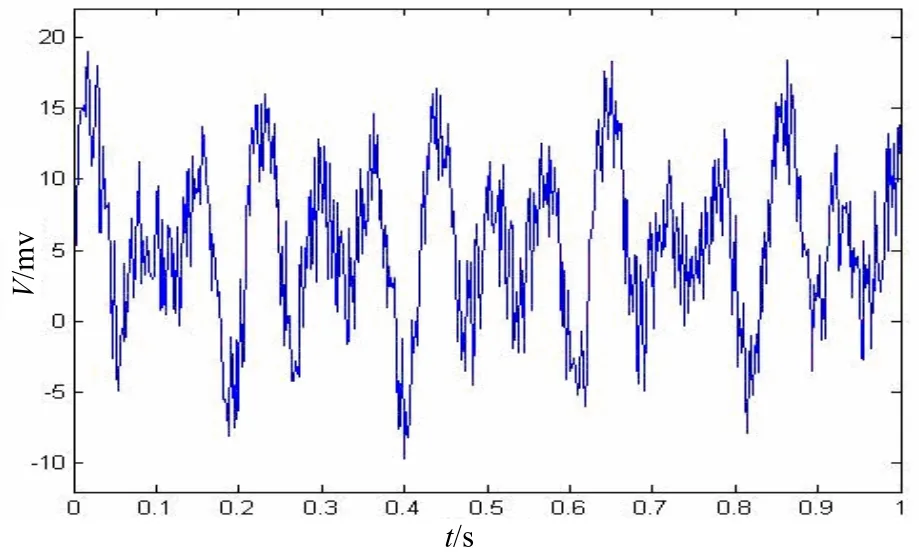
图2 染噪信号

图3 该新阈值决策去噪法的降噪信号

图4 软阈值函数去噪法的降噪信号

图5 硬阈值函数去噪法的降噪信号

5 结语

本文提出了一种新型阈值函数和自适应阈值的信号降噪法，仿真实验和应用实例显示该法可获得比常规传统硬阈值函数、软阈值函数的去噪方法更好的去噪效果，能更有效地提取有用微弱信号的信息。改进的小波阈值函数克服了软阈值信号失真和硬阈值不连续、振荡等缺点，提高了信号去噪的恢复能力。采用自适应的阈值算法能有效解决固定阈值产生过扼杀现象。试验证明该法提高了重构信号的信噪比，有效去除了噪声，且保留了原始信号的细节特征。

[1] DONOHO D L. De-noising by Soft-thresholding[J]. IEEE Transactions on Information Theory, 1995,41(03):613-627.

[2] 成礼智,王红霞,罗勇.小波的理论与应用[M].北京:科学出版社,2007(08):271-273.

[3] GERNIMO J S,HARDIN D P,MASSOPUST P R.Fractal Functions and Wavelet Expansions based on Several Scaling Functions[J].Journal of Approximation Theory,1994,78：373-401.

[4] 王睿,山拜达拉拜.一种新阈值函数的小波信号去噪研究[J].通信技术,2011,44(01):50-52.

[5] 易方,李著信,苏毅,等.基于改进型小波阈值函数的输油管道磁记忆信号降噪方法[J].石油学报,2009(01):141-144.

[6] 唐进元,陈维涛,陈思雨,等. 一种新的小波阈值函数及其在振动信号去噪分析中的应用[J]. 振动与冲击,2009(07):118-121.

[7] 李冠,吴尽昭,范明钰.基于小波的信号去噪分析[J]通信技术,2010,43(09):79-81.

[8] 段其昌,邓玉娟,应泽贵.基于改进阈值函数的小波包语音增强算法的研究[J].通信技术,2009,40(05):86-88.