双联挖泥船在宽水域施工中的共振分析
戚卫斌,倪海军
(浙江疏浚工程有限公司,浙江湖州 313000)
0 引言
多数现代挖泥船体为双联船体,当这种挖泥船在水库、湖泊、河口、近海等宽水域中进行施工作业时,必须考虑处于风成波浪中的船体共振问题,避免施工作业过程中产生灾难性后果.
宽水域水面在风力扰动下形成的波浪重力为恢复力,称为风成重力波,一般波高远小于波长,沿风力方向往前传播.对这种波浪的频率、波长、振幅进行研究与分析,对挖泥船的设计制造与购置时避免其固有频率与接近风成重力波的振动频率,从而避免施工作业过程的共振具有重要意义.
挖泥船的固有频率一般由制造厂家经试验与分析计算得出,使用者则必须对作业环境的具体施工水域进行风成重力波的频率分析,以防止施工过程中的共振发生.
1 风成重力波的频率分析
影响水面波浪特性的主要因素为水体重力,其他因素如粘滞力忽略不计,从而可以按照理想流体的势流理论来研究这种波浪运动的规律.
设想一简谐振动波沿水平方向x轴移动,且作如下假定:①水体不可压缩,重力作用存在;②运动无旋,仅具有速度势;③波动为微振幅线性波:波高远小于波长.
设波浪特性参数为:
h—水深,即平均水面至底部的垂直距离;
η(x,t)—波浪自由水面至平均水面的瞬时垂直距离;
H—波高,对小振幅波,H=2a,a为波浪振幅;
L—波长,即两个波峰或波谷之间的距离;
T—周期,即波浪传播一个波长所需要的时间;
C—波浪的传播速度;
K—在2π距离内传播的波长个数;
σ—波浪圆频率,在2π时间内波浪振动的次数.
1.1 线性波波面方程
按照波浪理论[1-3],微振幅线性波速度势函数φ(x,t)满足:

且满足拉普拉斯方程:

根据施工水域底部不可穿透条件认为:
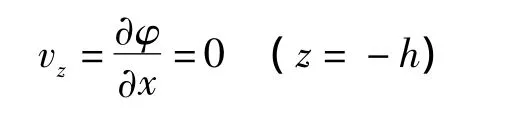
自由表面:

由laglange积分:

令:z=η,在自由表面压力P=0,为使波动线性化,使v2≈0则有:

则得到小振幅波的基本方程与边界条件为:
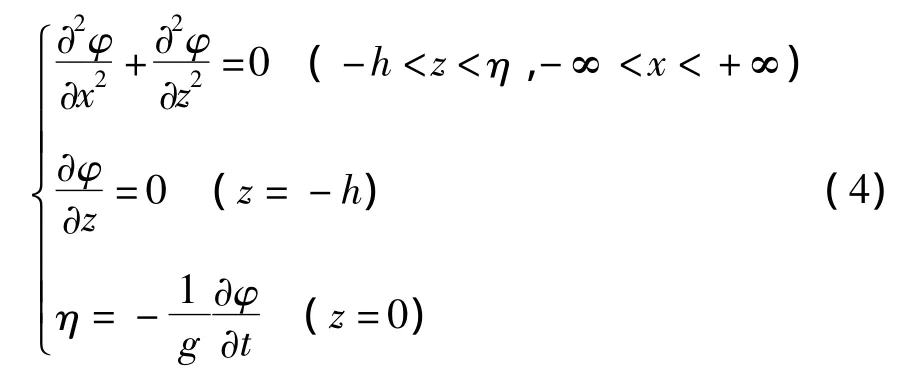
采用分离变量法求解得出速度势函数φ(x),并代入拉普拉斯方程得到:
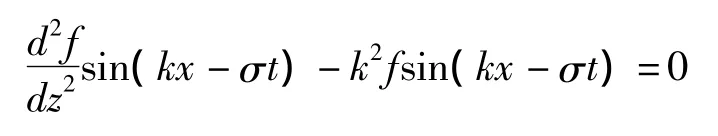
即:

式(5)的通解为:

故:
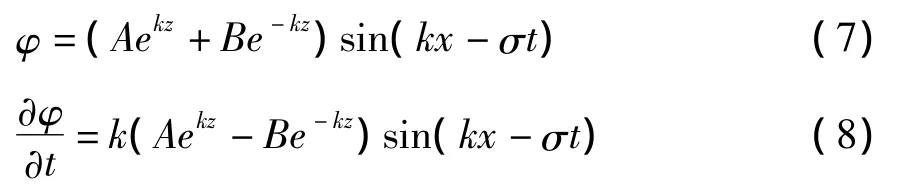
根据底部不穿透边界条件:

上式中的k与 sin(kx-σt)均不可能为0,故有:
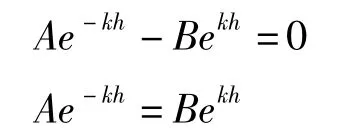
令:

得到:
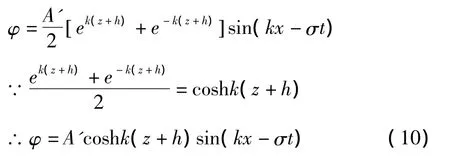
因此
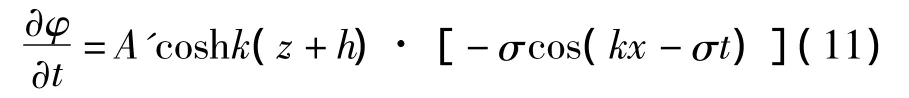
故:
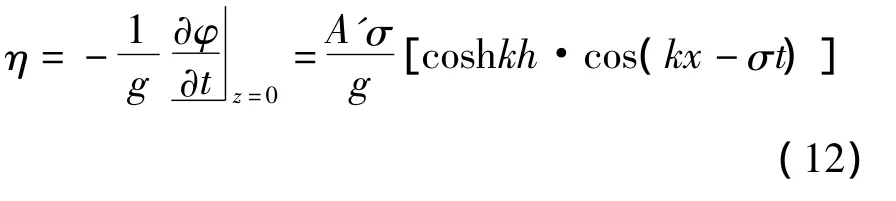
令:
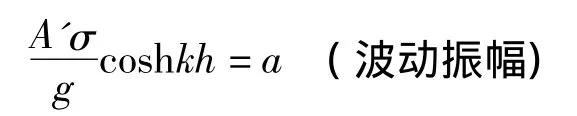
得到:
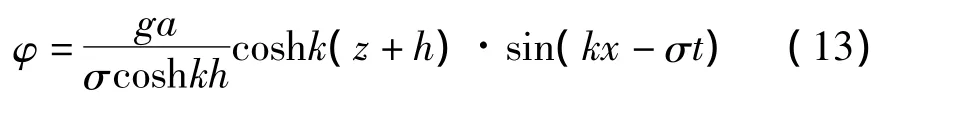
为此得到自由波面方程:

这是一个余弦波动方程.
当h→∞时:

有:

式(15)即为深水条件下的流速势函数,其波面方程为:

可见与式(14)是相同的.
1.2 波速、波长与周期
自由水面任何一点Z方向的速度分量为:

微振幅波沿X方向的坡度也是微量,即:
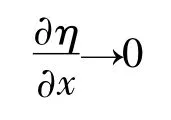
故:


对式(13)的速度势函数对Z求导得到:

对速度势函数(13)对t求二阶导数:

对照式(19)和式(21)得到:

根据式(19)的结论得到式(20)=(22),则有:

经化简得到:

将式(24)代入式(23)得到:

将k=2π/L代入上式得到波速计算公式:

该式中含有双曲正切函数tanh(2πh/L),该值具有以下特性[2]:
当水深h为 L/2≤h<∞时,tanh(2πh/L)→1.0;
当水深h为0<h<≤L/20时,tanh(2πh/L)→2πh/L;
当水深h为L/20<h<L/2时,tanh(2πh/L)=tanh(2πh/L).
为此,可将波速计算按三种不同水深进行近似分类:
当水深h为L/2≤h<∞时,称为深水波;
当水深h为0<h<≤L/20时,称为浅水波;
当水深h为L/20<h<L/2时,称为次深水波.
以上三种形式线性波的波速计算公式可分别写为:
深水波波速公式:

次深水波波速公式:

浅水波波速公式:

利用已知几个参数间的相互关系,同理可求得:

则波浪波动的频率可根据圆频率计算得出:

式(26)~(31)即为重力线性波频率分析的计算依据.
2 重力线性波的频率计算
根据式(26)~(31)针对宽水域中波长15~150 m的三种形式的重力线性波进行频率计算结果见表1.
从计算结果可以看出,无论深水波还是浅水波,其波动频率均在0.35 Hz以下.
3 共振分析
从以上计算结果可以看出,该船在不同水深条件下施工过程中水面重力线性波的振动频率均在0.35 Hz以下,而在一般情况下,双联挖泥船的固有频率多在1.20~14之间,例如某双联船体经有限元固有频率分析得出的结果为:在各个不同方向受外力作用时的固有频率范围在1.383 6~10.957 Hz之间,与水面重力线性波的频率差距均在20%以上,不可能产生共振.
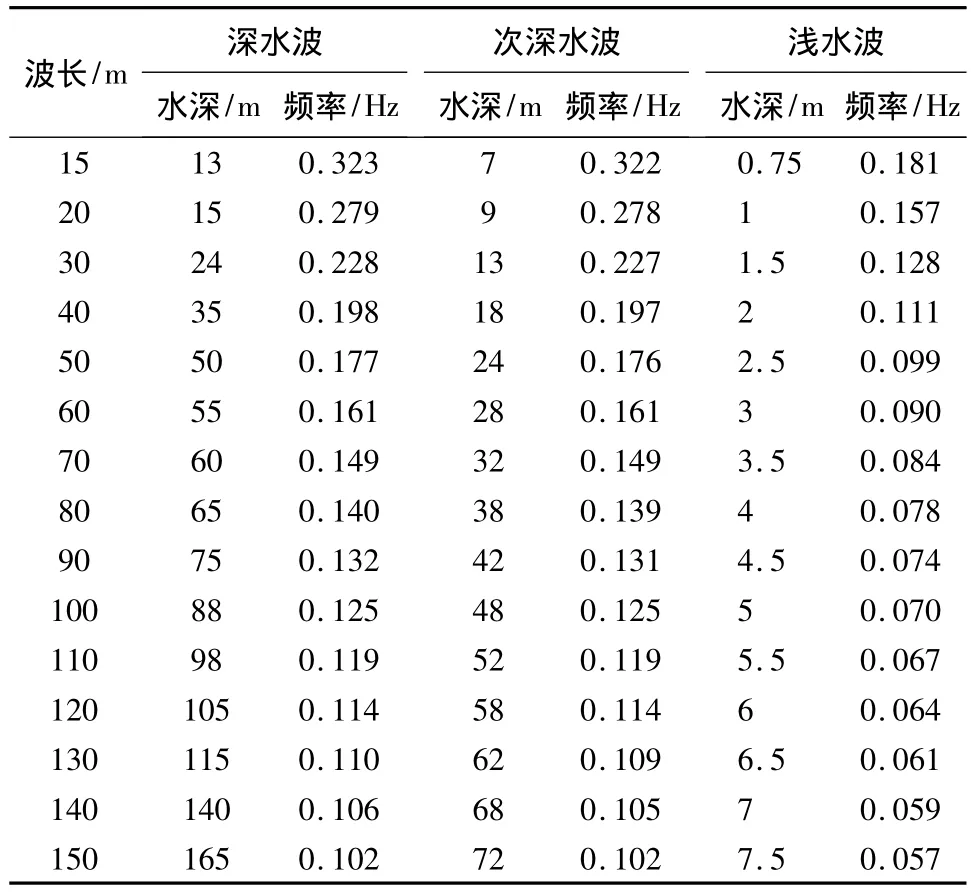
表1 重力线性波进行频率计算结果
4 结论
通过以上分析得出:双联挖泥船在河湖与近海等宽水域中疏浚施工作业时,当遭遇风成波作用时不存在共振风险.
[1]李远林.波浪理论及波浪载荷[M].广州:华南理工大学出版社,1994.
[2]竺艳蓉.海洋工程波浪力学[M].天津:天津大学出版社,1991.
[3]毕家驹.近海力学导论[M].上海:同济大学出版社,1989.

