房间空调器缩小换热器管径的表面反应设计方法

吴照国 任 滔 丁国良 胡海涛 郑永新 高屹峰

(1 上海交通大学制冷所 上海 200240 2 国际铜业协会（中国）上海代表处 上海 200020)

房间空调器缩小换热器管径可以减少材料消耗，降低换热器的成本，同时，也可以减少制冷剂的充注量，降低制冷剂对环境的影响。目前，房间空调器产品主要采用9.52mm或者7mm的铜管。若将管径由9.52mm缩小为5mm， 单位管长铜管的表面积和内容积分别减少47.4%和75.4%。这就意味着，即使铜管的厚度不变，单位管长的铜用量减少47.4%。实际上，由于耐压强度增加、铜管壁厚减薄，单位管长的铜材可减少62.9%、制冷剂充注量可减少73.6%。

但是，缩小换热器管径会对换热器产生以下三个方面的影响。首先，缩小换热器管径会引起管内制冷剂压降急剧增加[1-3]。其次，由于翅片翻边等加工工艺的限制，缩小换热器管径会引起翅片翻边尺寸和翅片间距减小，增加空气侧风阻，从而使得空气的风量和换热性能降低[4-5]。最后，缩小换热器管径会导致翅片尺寸减小[6]，使得翅片换热面积减小，从而导致空气侧换热性能减低。上述的三个影响均会造成换热器换热性能的下降，因此，需要针对以上因素对缩小管径的换热器进行设计。

缩小管径的换热器设计的有效方法为：1)在考虑制造工艺的前提下对分路数进行优化设计，使单个分路的制冷剂流量和压降保持在合理范围内[7]；2) 减小翅片间距和增加换热管数目，来增加翅片的换热器面积，从而保证换热器的性能；3)在调整翅片间距和增加的换热管长度时，需考虑换热器的成本最优且性能达到设计要求。传统的实验设计方法由于样机制造和测试繁琐，不适用于实际设计，因此，需要采用换热器仿真优化方法来进行缩小管径后的换热器优化设计。

表面反应法[16]是可以同时对多个变量在连续区间变化时进行寻优的方法。该方法可以根据连续区间内多个变量的有限离散点进行二次连续函数拟合，从而反应各个变量在连续区间内的变化，以及各个变量之间的相互关系。该方法在航空[17]、化学[18]、机械[19]等行业方面得到应用，同时也已应用于换热器结霜工况下的翅片间距优化[20]。但目前没有关于表面反应法应用于换热器优化设计研究的报道。

因此，结合表面反应法对管径缩小后的换热器进行优化设计。采用基于图论的换热器三维分布参数模型对离散点的换热量进行计算，通过换热器稳态分布参数模型和流路优化方法提供表面反应法拟合所需离散点的参数，实现管长和翅片间距在连续区间内变化时换热量的拟合及其换热器设计目标的寻优求解。

1 换热器表面反应设计法

1.1 换热器优化的目标

房间空调换热器的结构示意图如图1所示，其中：fp为翅片间距，H为换热器高度，L为换热器宽度，N为换热器分路数，Pl为纵向管间距，Pt为横向管间距，W为换热器宽度。上述结构参数可描述为x向量的形式，如公式（1）所示。

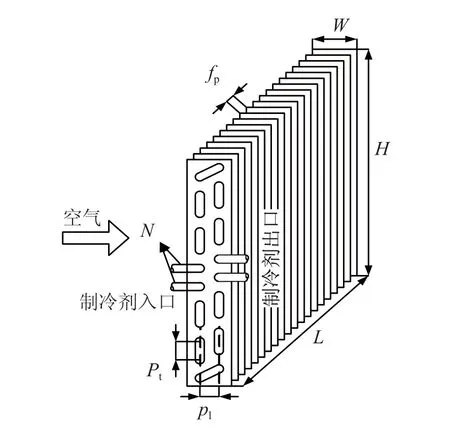
图1 房间空调换热器的结构示意图Fig.1 Skeleton drawing of room air conditioner heat exchanger

房间空调器缩小换热器管径后，为了达到节约成本和减少制冷剂充注量，其设计目标为：换热性能达到设计要求且成本为最优。考虑到实际设计过程中换热器磨具和加工工艺等限制，向量x中的变量通常要求在一定的范围内变化，因此，房间空调器缩小换热器管径后的设计目标可用数学形式进行描述，如方程（2）所示。

式中：F(x) —换热器的成本；Q(x) —换热器的换热量；Qref—换热器换热量的设计目标；xmin,xmax—x的最小值和最大值。

依托校企共建生产性实训基地，开展校企产教融合。结合专业实训基地条件，与通信企业对接，在真实的工作环境和生产性项目中，实现“教、学、产、研”一体的生产性实训，进一步提高人才培养的技能水平和职业素养。由企业工程师、专任教师担任实训指导教师，将企业工程案例融入课程内容，指导学生分析项目、实施项目、验收项目等内容，实现学校教学环境和企业真实工作环境的对接。利用基地先进的设备和软件、优秀的师资团队通过企业承担实际工程项目，选拔优秀学生共同参与，让学生将课堂环境与企业真实工作环境一致，真正做到学校教学内容与工作内容的零距离结合。

为提高缩小管径后的设计精度，需要准确地计算方程(2)中的变量，从而进行方程的求解。由于方程中Qref, xmin和xmax均为换热器设计的已知参数，因此，换热量Q(x)的准确性将直接影响换热器设计的精度，需要在连续区间[xmin, xmax]内对采用不同x的换热器换热量进行准确计算，其计算过程先通过确定连续区间内离散点换热器的分路数和换热量，并根据离散点换热量拟合连续区间的换热量。

1.2 分路数确定

房间空调换热器的制冷剂压降与质流密度的关系如公式（3）所示。

式中：S —当量流阻常数；G —质流密度；L—流程长度。

缩小换热器管径后，若压降保持不变，则∆p的全微分应为0。因此，压降关于管径di，换热器分路数N和换热器总管程长度Lt的全微分等于0，如公式（4）所示。经计算取整后得出制冷剂分路数与管径的关系式如公式（5）。

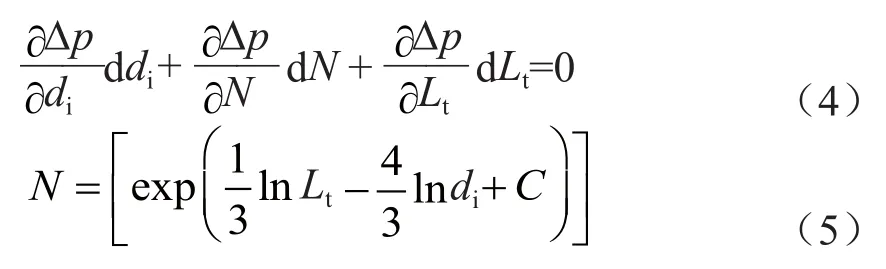
式中：C —常数；di—换热器的管径；Lt—换热器的总管长；N —换热器的分路数。

1.3 离散点换热量计算

采用基于图论的换热器三维分布参数模型[10]对离散点的换热量进行计算。该模型对单个控制单元的制冷剂侧和空气侧参数进行双重迭代计算，同时对整个换热器的换热和压降采用交替迭代的算法，并利用图论的方法对管路进行描述，该模型经实验验证能准确预测换热器性能。换热器模型的数学描述如论文[10]的公式(1)～(18)所示。

为了保证连续区间[xmin, xmax]内缩小管径后换热器的换热量Q(x)的拟合精度，拟合所需离散点换热量数目n的计算公式如（6）所示。

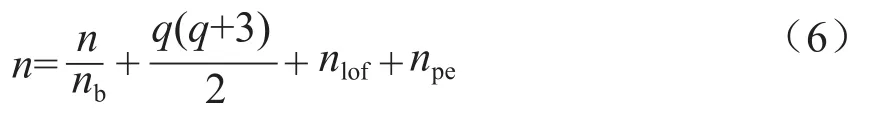
式中：nb— 实验分组数目；q — 拟合变量的个数；nlof— 小量，通常为5～10，用来估计缺失的拟合量；npe— 小量，通常5～15，用来估计数据点的误差。

1.4 连续区间内换热量拟合

通过换热量离散点对连续区间内换热量进行拟合时，需要先对X进行归一化，如公式（7）所示：

式中：xref—上下限间的中点值，归一化后变量Xi的取值范围为Xi∈[-1,1]。

根据归一化后自变量的Xi，采用表面反应函数f(X)对进行Q(x)的二次连续函数拟合，拟合后的形式如方程（8）所示。其中β为需要拟合的常量参数。

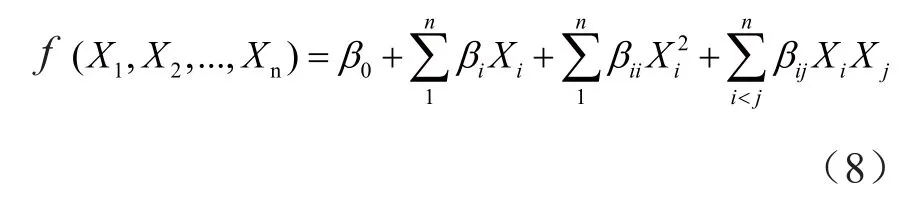
经过自变量的归一化和换热量的表面反应法拟合，缩小换热器管径的设计目标方程(2)转化为具有二次连续函数约束并可直接求解的连续函数方程(9)，通过最值求解法即可得出缩小换热器管径的设计结果。

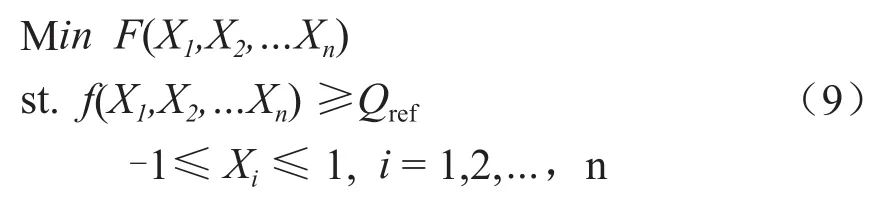
式中：Xi— 归一化的结构参数；F(Xi) —换热器成本函数；f (Xi) —换热量的表面反应函数；Qref—换热量的设计目标。

2 计算实例验证与方法应用说明

房间空调器换热器包括蒸发器和冷凝器两部分。其蒸发器几乎均是采用一块I型换热器（窗式空调器）或者多块I型换热器的组合（分体式空调器），而占房间空调器市场绝大部分份额的冷凝器均采用L型换热器。

为了进一步说明换热器的表面反应设计方法，这里举出I型和L型的翅片管换热器缩小管径后的设计算例。对于设计方法的准确性验证采用I型换热器设计结果与实际验证结果进行对比说明，同时，对于设计方法的实际意义采用L型换热器设计结果进行分析。

2.1 计算实例

以7mm管I型换热器和9.52mm管L型换热器为例，分别将两款换热器的管径均缩小为5mm管进行算例说明。7mm管I型换热器和9.52mm管L型换热器的结构示意图如图2所示，其结构参数如表1所示。

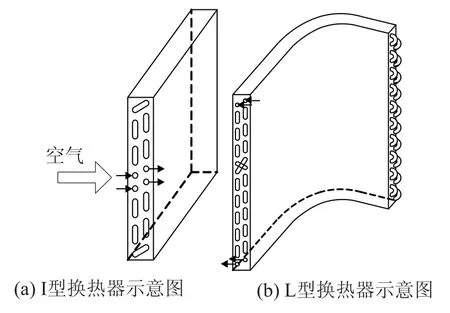
图2 I型和L型换热器示意图Fig.2 Skeleton drawing of I type and L type heat exchangers

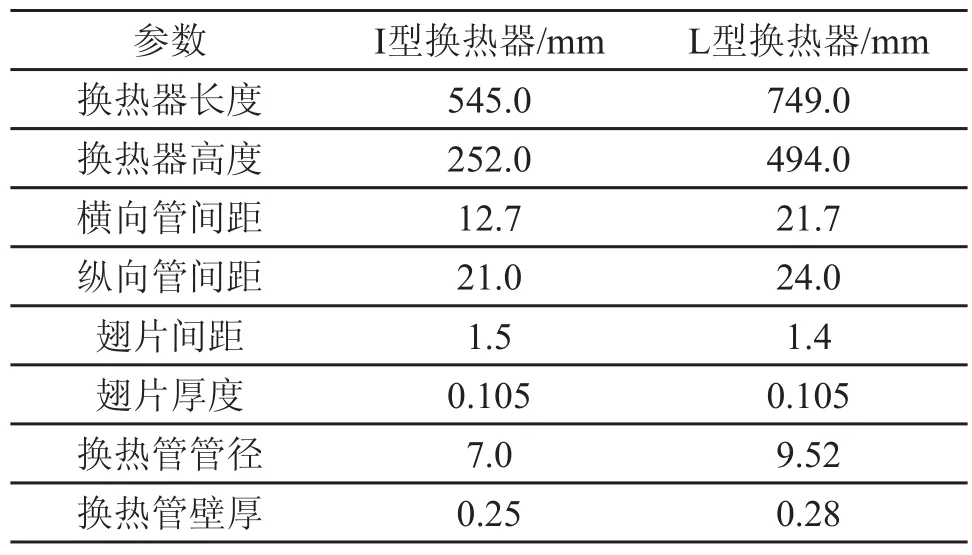
表1 I型和L型换热器结构参数Tab.1 Structure parameters of I type and L type heat exchangers

根据公式（5）和（6）可知：将7mm管I型换热器和9.52mm管L型换热管的管径均缩小为5mm后，I型换热器为3分数路，拟合需要27个数据点；L型换热器为5分数路，拟合需要27个数据点。换热器拟合时换热管管长L和翅片间距fp的变化范围如表2所示。

表2 L和fp的范围取值Tab.2 Range of L and fp

根据表2参数和公式(7)将L和fp归一化为X1和X2。利用基于图论的三维稳态分布参数模型[10]对两个换热器拟合所需数据的换热量求解，根据公式(8)和(9)进行换热量拟合和转化，得出管径缩小为5mm管后的I型换热器和L型换热器的设计目标方程分别如公式(10)和(11)所示。

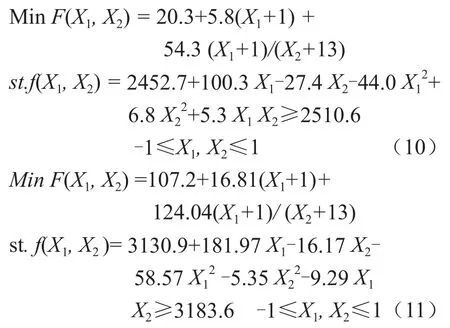
通过对方程(10)和(11)求解，可得出管径缩小为5mm管后I型换热器和L型换热器的设计结果参数如表3所示，其结构如图3所示。

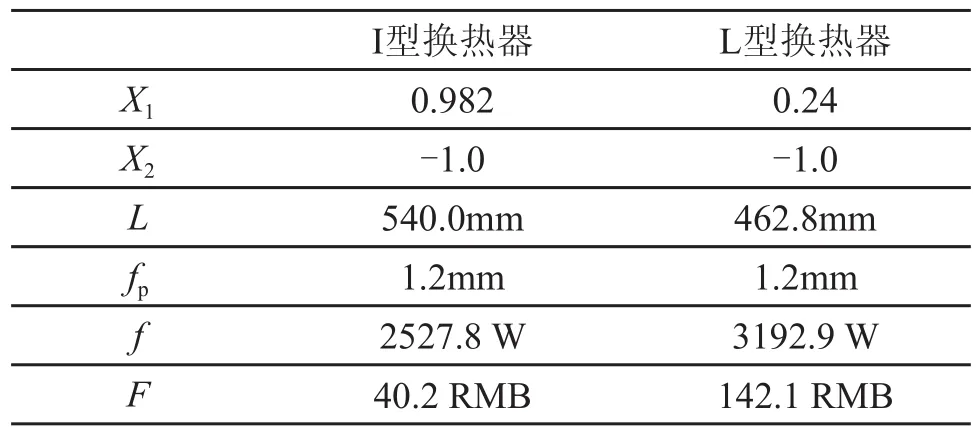
表3 管径缩小后I型和L型换热器的计算结果Tab.3 Parameter results of I type and L type heat exchangers after decreasing tube diameter

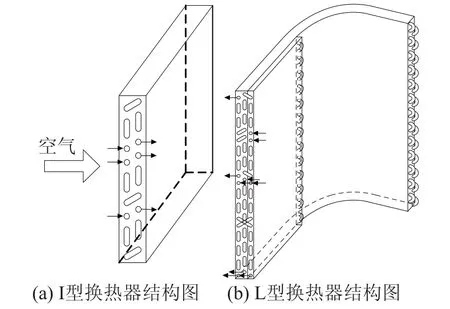
图3 缩小管径后I型和L型换热器结构示意图Fig.3 Skeleton drawing of I type and L type heat exchangers after decreasing tube diameter

2.2 方法准确性验证

为了说明设计方法的准确性，采用缩小管径后I型换热器的设计结果与实验测试结果进行分析。实验测试采用焓差法对I型换热器的换热量进行测试，其测试工况与设计工况相同，均为国家标准GB/T7725—2004[21]《房间空气调节器》的额定测试工况。实验测试结果如表4所示。

由表4可知，管径缩小后I型换热器换热量的设计结果与实验结果偏差0.3%；通过分析可知管径缩小后换热器成本下降了26.9%。即：采用表面反应设计法对缩小换热器管径进行设计时，能准确预测换热性能并有效降低成本。

表4 I型换热器设计结果与实验测试结果对比Tab.4 Result comparison of design and experiment of I type heat exchanger

2.3 方法应用说明

为了说明设计方法的实际意义，对缩小换热器管径后L型换热器的设计结果进行分析。根据公式(11)进行绘图，得出换热管管长和翅片间距分别与成本、换热量的关系示意图如图4和图5所示。

由图4可知,1) 管长变化对成本的影响远大于翅片间距变化对成本的影响，其原因为：L型换热器每列换热管数目较多，且铜材价格为铝材价格的3倍；2) 翅片间距的变化对换热器成本的增加不明显，其原因为：L型换热器铜管和翅片数目多，换热器成本较高，使得翅片间距在小范围内变化时，对成本影响较小。

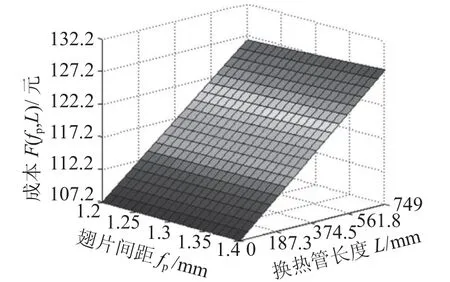
图4 换热管管长、翅片间距和成本关系示意图Fig.4 Relationship of heat exchanger cost with tube length and fi n pitch

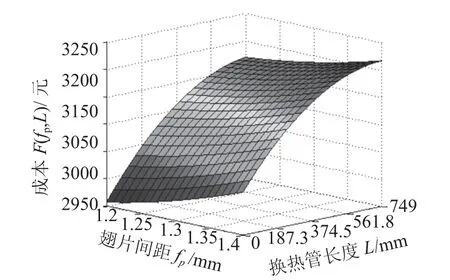
图5 换热管管长、翅片间距和成本关系示意图Fig.5 Relationship of heat exchange capacity with tube length and fi n pitch

由图5可知：1) 管长变化对换热量的影响远大于翅片间距变化对换热量的影响，其原因为：管长的变化可以引起管内外换热面积，以及换热器内制冷剂充注量的变化；2) 随着管长的增加，换热量增加率将会由大到小变化。其原因为：换热器管长增加将使得换热器过冷度也随之增加，使得换热器过冷区长度增长，从而导致管长增加后有效换热长度减小。

利用换热器模型[10]对管径缩小前L型换热器和管径缩小后L型换热器进行计算，得出换热器的性能参数如表5所示。

由表5可知：相对于管径缩小前的L型换热器，缩小换热器管径后设计换热器的换热量仅减少了0.6%，过冷度降低了0.5℃，压降在合理范围。同时，缩小换热器管径后换热器的成本降低了28.0%，制冷剂充注量减少了39.8%。

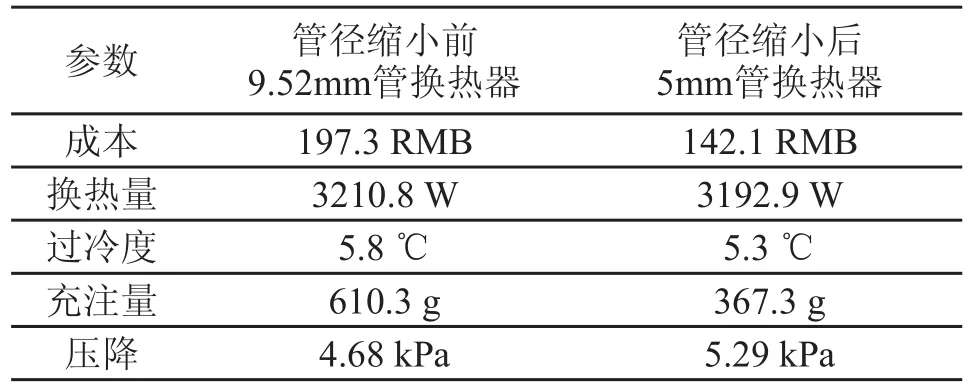
表5 管径缩小前后L型换热器的性能参数Tab.5 Performance of L type heat exchanger after decreasing tube diameter

3 结论

提出采用表面反应法对换热器进行优化设计的方法。在该方法中，采用基于图论的换热器三维分布参数模型对离散点的换热量进行计算，采用表面反应法拟合所需离散点的参数，实现管长和翅片间距在连续区间内换热量和成本的寻优求解。

通过对I型换热器进行管径缩小的优化设计，其设计结果与实验结果相差0.3%，从而验证了该方法的准确性。

采用提出的基于表面反应法的设计方法，对L型换热器进行优化设计，在保证热性能不变的前提下，换热器管径从9.52mm缩小为5mm，成本可降低28.0%，制冷剂充注量可减少39.8%。

在缩小换热器管径的设计中，管长变化对换热器成本和换热量的影响远大于翅片变化对其影响。但随之管长的增加，使得换热器过冷区长度变长，换热量增加率将变小。

[1]胡海涛,丁国良,黄翔超,等.小管径强化管内R410A-油混合物流动沸腾阻力特性[J].上海交通大学学报，2008, 42(5): 394-398. (Hu Haitao，Ding Guoliang，Huang Xiangchao, et al.Flow Resistance Characteristics of R410A-oil Mixture during Evaporation in a Small Diameter Enhanced Tube[J]. Journal of Shanghai Jiao Tong University,2008,42(5): 394-398.)

[2]Hu H T，Ding G L，Wang H J. Measurement and Correlation of Frictional Pressure Drop of R410A/Oil Mixture Flow Boiling inside a 7mm Straight Microfin Tube[J].Applied Thermal Engineering，2008，49(11)：1272-1283.

[3]魏文建,丁国良,王凯建,等.含油制冷剂在小管径换热管内流动沸腾换热特性实验研究[J].上海交通大学学报,2006,41(3):404-410. (Wei Wenjian,Ding Guoliang,Wang Kaijian, et al. Experimental Study on the Influence of Oil on Heat Transfer Performance of Refrigerant Flow Boiling Inside Small Tubes[J]. Journal of Shanghai Jiao Tong University,2006,41(3): 404-410.)

[4]刘建,魏文建,丁国良,等. 翅片管式换热器换热与压降特性的实验研究进展—实验研究[J].制冷学报,2003,24(3): 25-30. (Liu Jian,Wei Wenjian,Ding Guoliang, et al. Development of Study on Heat Transfer and Friction Characteristics of Fin-and-Tube Heat Exchanger-Experimental Study[J].Journal of Refrigeration,2003,24(3): 25-30.)

[5]刘建,魏文建,丁国良,等.翅片管式换热器换热与压降特性的实验研究进展—关联式[J].制冷学报, 2003,24(4): 21-27. (Liu Jian, Wei Wenjian, Ding Guoliang,et al.Development of Experimental Research on Heat Transfer and Friction Characteristics of Fin-andtube Heat Exchanger-Correlation[J]. Journal of Refrigeration,2003,24(4): 21-27.)

[6]Wang C C, Jang J Y. Effect of Circuit Arrangement on the Performance of Air-Cooled Condensers[J].International Journal of Refrigeration, 1999, 22(4): 275-282.

[7]Wang C C, Lee C J, Chang C T. Heat Transfer and Friction Correlation for Compact Louvered Fin-and-Tube Heat Exchangers[J]. International Journal of Heat and Mass Transfer, 1998, 42(11): 1945-1956.

[8]Domanski P A. Simulation of an Evaporator with Non-Uniform One-Dimensional Air Distribution[J]. ASHRAE Trans, 1991,97(1): 793-802.

[9]Jiang H B, Vikrant Aute, Radermacher R. CoilDesigner:A General-Purpose Simulation and Design Tool for Airto-Refrigerant Heat Exchanger[J]. International Journal of Refrigeration, 2006, 29(5): 601-610.

[10]Liu J, Wei W J,Ding G L,et al. A General Steady State Mathematical Model for Fin-and-Tube Heat Exchanger Based on Graph Theory[J].International Journal of Refrigeration, 2004, 27(8): 965-973.

[11]Domanski P A, Yashar D. Optimization of Finned-Tube Condenser Using An Intelligent System[J].International Journal of Refrigeration, 2007, 30(11): 482-488.

[12]Wu Z G, Ding G L, Wang K J, et al. Knowledge-Based Evolution Method for Optimizing Refrigerant Circuitry of Fin-and-Tube Heat Exchangers[J].HV&AC Research,2008, 14(6): 140-150.

[13]彭波涛, 罗来琴, 王秋王, 等. 多股流板翅式换热器的微分与优化数值研究[J].化工学报,2004,55(3):876-881.(Peng Botao,Luo Laiqin,Wang Qiuwang, et al. Numerical Study of Differential and Optimal Design for Multi-Stream Plate-Fin Heat Exchanger[J]. Journal of Chemical Industry and Engineering(China),2004,55(3):876-881.)

[14]Matos R S，Laursen T A，Vargas J V C，et al. Three-Dimensional Optimization of Staggered Finned Circular and Elliptic Tubes in Forced Convection[J].International Journal of Thermal Sciences，2004，43(12)：477-487.

[15]Lee K S,Oh S J. Optimal Shape of the Multi-Passage Branching System in a Single-Phase Parallel-Flow Heat Exchanger[J].International Journal of Refrigeration,2004, 27(3): 82-88.

[16]Andre K. Response Surface Methodology and Related Topics[M].World Scienti fi c, 2006.

[17]Goel T, Vaidyanathan R, Raphael T, et al. Response Surface Approximation of Pareto Optimal Front in Multi-Objective Optimization[J].Computer Methods in Applied Mechanics and Engineering, 2007, 196(35): 878-893.

[18]Sharma S, Malik A, Satya S. Application of Response Surface Methodology for Optimization of Nutrient Supplementation for Cr (VI) Removal by Aspergillus Lentulus AML05[J].Journal of Hazardous Materials,2009, 164(23): 1198-1204.

[19]Shokuhfar A, Khalili S M, Ghasemi A, et al. Analysis and Optimization of Smart Hybrid Composite Plates Subjected to Low-Veloctiy Impace Using the response Surface Methodology[J].Thin-Walled Structures, 2008,46(3): 1204-1212.

[20]Yang D K, Lee K S,Song S. Fin Spacing Optimization of A Fin-Tube Heat Exchanger under Frosting Conditions[J].International Journal of Heat and Mass Transfer,2006,49(8): 2619-2625.

[21]国家标准局信息分类编码研究所.GB/T 7725—2004.房间空气调节器[S].北京: 中国标准出版社, 2004.