基于Level Set的交互式快速分割算法

孙海鹏， 余伟巍， 席 平



基于Level Set的交互式快速分割算法

孙海鹏， 余伟巍， 席 平

（北京航空航天大学机械工程及自动化学院，北京100191）

三维医学图像数据量大，并且受噪声、边界模糊等原因的影响，致使三维分割过程消耗时间较长，容易产生欠分割或过度分割。针对以上问题，提出一种基于Level Set的三维快速分割算法，采用Fast Marching获取二维分割区域，优化轮廓边界，利用直线数值微分算法（Digital Differential Analyzer，DDA）提取轮廓像素；进一步引入扫描线种子填充思想，实现医学图像的三维快速分割。实验结果表明，上述算法能够快速准确地分割出感兴趣区域。

计算机应用；医学图像三维分割；Level Set算法；数值微分算法；扫描线种子填充

医学图像分割技术，是图像分割领域中一个重要分支，自上世纪90年代起一直受到学术界的广泛重视，是虚拟手术系统中不可缺少的一个重要组成部分，为结构分析、运动分析和三维可视化等提供基础数据来源，分割结果的有效性直接影响最终虚拟手术结果的有效性。

目前主流医学图像分割算法大多针对二维医学图像，如：M Kass提出的Snakes算法，它是用能量最小化作为框架，通过定义内能和外能来模拟物理上的力学原理最终实现医学图像的分割，但snake算法受能量函数的初始状态影响较大；Osher和Sethian提出的Level Set算法，它将曲线演化问题转化为偏微分方程数值求解问题，具有很强的处理拓扑结构变化的能力，但Level Set的计算复杂度较高。针对Level Set算法计算复杂度较高的问题，提出了快速水平集算法(Fast Marching Level Set Method)；此外，还有一些基于结合特定理论的分割方法，如：基于数学形态的图像分割，基于模糊技术的图像分割，基于神经网络的图像分割，基于知识的图像分割等。但为了实现构造三维医学图像需要多次进行二维医学图像分割，比较耗时，并且每次二维医学图像分割结果都极大地影响到三维医学图像的精确性。

然而，现有的直接针对三维体数据分割，例如基于6联通区域增长法，算法耗时长，且容易出现欠分割或过度分割等情况。

针对以上问题，本文在分析和融合多种分割算法的基础上，面向三维医学图像分割，提出一种基于Level Set的三维快速分割算法，采用Fast Marching 快速步进获取二维分割区域，优化轮廓边界，利用直线扫描数值微分算法（DDA）方式提取轮廓像素，引入扫描线种子填充思想，实现医学图像的三维快速分割，有效解决了三维医学图像分割过程中所耗时间长、易产生欠分割和过度分割的问题。

1 Level Set算法

Level Set算法的基本思想是将平面闭合曲线隐含地表达为二维曲面函数的水平集，即具有相同函数值的点集，通过水平集函数曲面的进化隐含地求解曲线的运动。尽管这种转化使得问题在形式上变得复杂，但在问题求解上带来很多优点，其最大的优点在于曲线的拓扑变化能够得到很自然地处理，而且可以获得唯一的满足熵条件的弱解。

水平集函数的演化满足如下基本方程

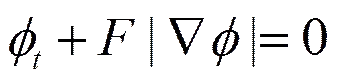
Φ(x, t)为水平集函数，Φ(x, t=0)为初始设置的演化曲线，其零水平集表示目标轮廓线，即

（2）

Level Set算法中最典型的一种算法是FastMarching算法。Fast Marching算法只考虑一种界面运动的特殊情况，即界面的运动速度>0。假定是界面经过一个指定点(x, y)的时间，这样，就满足如下的方程

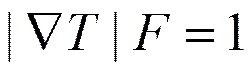
式(3)简单地说明了到达时间的梯度和界面的运动速度成反比。广义上说，有两种方法可以用来求解近似运动界面随时间变化的位置：一种是通过迭代和数字近似来获取式(1)中的微商；另一种是构建式(3)中到达时间T的解决方案。而快速水平集算法依赖于后一种方法。

要得到式(3)中的到达时间，等价于求解下面的二次方程

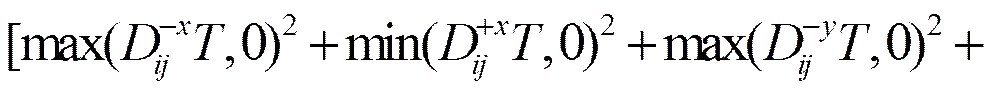
（4）

由于式(4)差分法的结构决定演化曲线传递的信息是单向的，也就是时间由小到大的传递过程。因此，求解式(4)采取从最小的时间向外求解过程。

Fast Marching算法的过程分为初始化和循环。

初始化：

（1）活动点 是指所有网格点中时间固定的点。在此算法中即用户指定的种子点P，表示时间T(x, y)=0，如图2黑色方格所示；

（2）窄带点 所有在窄带中的点叫做窄带点。在此算法中就是所有种子点的4-邻接的点，时间T(x, y)=1/F(x, y)，如图2灰色方格所示；

（3）远离点 除了活动点和窄带点以外，所有其他的网格点都是远离点，T(x, y)=TIME_ MAX，如图2白色方格所示。

(a)     (b)      (c)

循环：

（1）开始循环，假定点P是窄带中具有最小时间T的点；

（2）标定点P为活动点，并从窄带中删除；

（3）标定点P的4-联通点：如果点P的邻接点为活动点，则不改变时间；如果其邻接点为窄带点，则按照公式(4)更新邻接点的时间；如果其邻接点为远离点，则标定该邻接点为窄带点，同时按照公式(4)更新该邻接点的时间；

（4）如果某一点的到达时间超过指定的限值，则循环结束，否则跳到(1)。

依据Fast Marching算法对关键层图像进行分割，分割结果如图3所示。

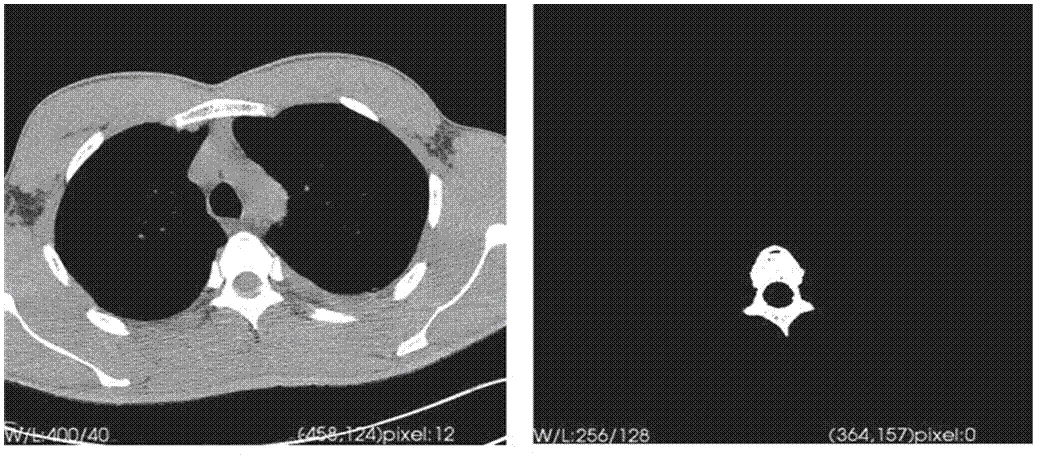
(a) 所选关键层医学图像     (b) 关键层分割结果

2 轮廓追踪与轮廓精简

为了得到图像的外部特征，关键层图像在Level Set算法分割过程中进行了二值化处理，得到目标轮廓的单值区域，通过对该单值区域的轮廓追踪，得到目标轮廓的外部轮廓点。

2.1 轮廓追踪

本文提出的轮廓追踪方法，其基本原理如下：

首先将轮廓上最左下方的点作为轮廓搜索的起始点。其次按照下述的“探测准则”来寻找目标轮廓上的其它像素。

探测准则：从第1个边界点开始，定义初始的搜索方向为左上方；如果左上方的点是黑点，则为这个边界点的新的边界点，否则，搜索方向顺时针旋转45°。直到找到第1个黑点为止。之后把这个黑点作为新的边界点，在当前方向上逆时针旋转90°，继续同样的方法搜索下一个黑点,直到返回最初的边界点。如图4所示。

追踪算法对图3(b)进行追踪结果如图5所示。

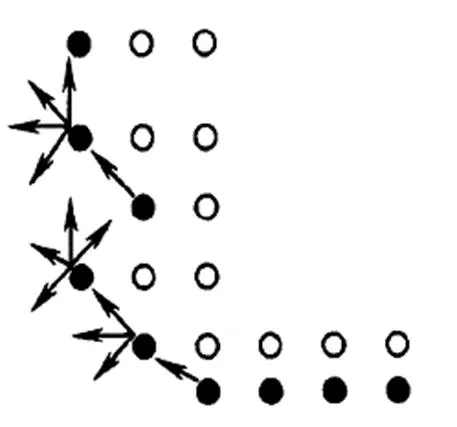
图4 轮廓追踪法示意图 (箭头代表搜索方向)

图5 轮廓追踪结果

2.2 轮廓精简

在轮廓追踪过程中，目标轮廓的每一个像素点都被存储，因此造成较大的数据冗余。为方便以后轮廓曲线的调整，必须对追踪结果进行精简。目前提出的轮廓精简算法主要有等距采样法和曲率采样法两种，但是前者会导致大量特征点的丢失，而后者因为曲率计算公式会涉及2 级导数的计算，比较复杂。因此，本文采用“弦差法”进行轮廓精简，“弦差法”的原理如图6所示。

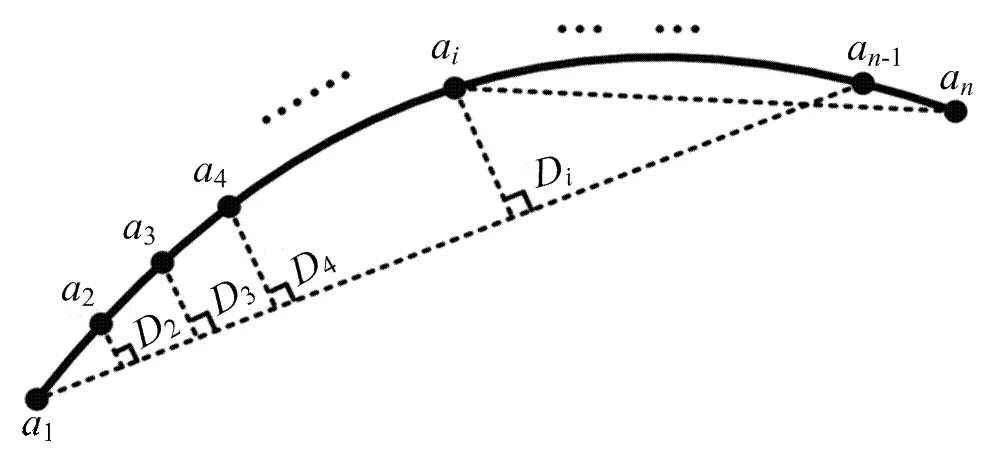
图6 “弦差法”原理

首先定义距离阈值ΔD描述轮廓精简的精度，然后取a作为轮廓精简的起点，a为终点，计算a到aa的距离D，如果D<ΔD，说明点a在控制弦差范围之内，终点加1，变为a，计算点a, a到弦aa的距离，比较D，D与距离阈值ΔD之间的大小，依次循环，直到起点a和终点a之间的点到弦aa的距离D>ΔD为止，此时说明a和a之间的点已经超出了精度控制范围，因此可将a作为轮廓精简点予以保留，而a和a之间的点可以舍弃，把a作为起始点，重复以上的步骤，寻找下一精简点。

依次循环，直到遍历所有轮廓点，精简结束。图7是运用上述方法取距离阈值ΔD= 0.6时对图5进行轮廓精简后的输出图像，精简前轮廓点数为429，精简后轮廓点数为35，从精简结果可以看出，精简后图像与精简前图像形状极其一致，而点的数据量大大减少，因此精简效果十分明显。

图7 轮廓精简结果

3 构造轮廓曲面

3.1 生成Bézier轮廓曲线和投影

3.1.1 Bézier曲线

Bézier曲线是1962年贝齐尔提出的一种参数多项式类型的构造曲线的方法。

由于处理作为顶点的绝对矢量比Bézier多边形边的相对矢量方便；故本文使用英国的弗里斯特改写Bézier曲线方程如下

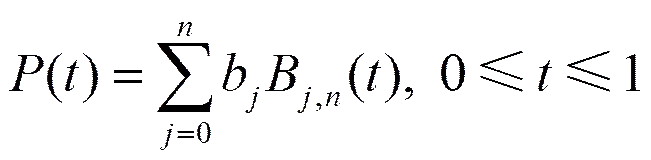
（6）

3.1.2 构造Béizer轮廓曲线及投影

如直接利用在2.2节中的轮廓精简方法得到的一系列的轮廓点构造Bézier曲线会造成曲线次数较高，调整轮廓形状不方便等不良效果。因此，将精简后的两两相邻的轮廓点作为一段Bézier曲线的起始控制顶点和终端控制顶点，分段构造轮廓Bézier曲线。

两个控制顶点仅仅可以构造1次Bézier曲线，为了得到更好的光顺性，需人为地在始末控制顶点间添加两个控制顶点，满足构造3次Bézier曲线的要求。添加控制顶点及构造Bézier轮廓曲线过程如图8所示。

图8 添加Bézier曲线控制顶点示意图

其中、、、、、为精简后的控制顶点，取与的连线，在连线上取点，使点满足以下条件

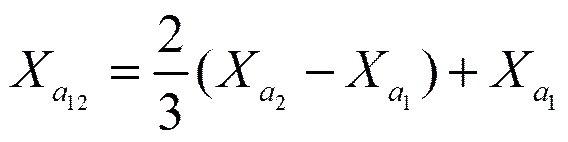
取与的连线，在连线上取点，使点满足以下条件

（8）

再取与的连线，在连线上取点，使点满足以下条件

取与的连线，在连线上取点，使点满足以下条件

（10）

以此类推可以人为地在精简后的两个相邻控制顶点间添加两个新控制顶点，以如(,,,)，(,,,)…(,,,)等为控制顶点分段构造3次Bézier曲线。

如图9所示为构造的3次Bézier样条曲线示意图

图9 构造3次Bézier样条曲线示意图

图10为运用上述构造轮廓曲线方法对图7精简轮廓后的控制顶点构造Bézier轮廓曲线的结果图。

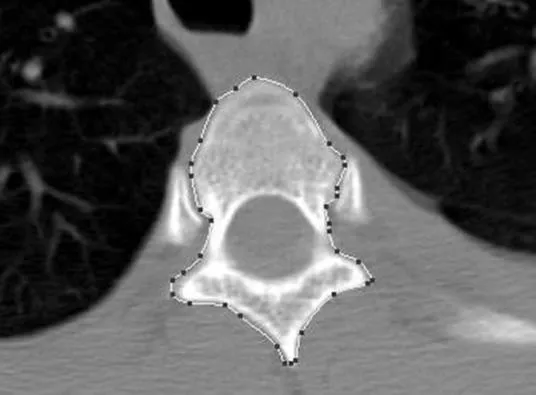
图10 构造Bézier轮廓曲线

由于待分割目标轮廓在某截面方向上轮廓大体相似，故将关键层的轮廓曲线沿与关键层面相垂直的轴向投影便可得到待分割目标的大致体轮廓。本文以横切面和方向为例，以CT切片组的方向的切片间距为增量，将之前得到的Bézier轮廓曲线沿方向在整个CT切片组空间中进行投影，得到一组Bézier轮廓曲线族。如图11所示。

图11 Bézier轮廓曲线投影

3.2 DDA轮廓插值及构造轮廓曲面

虽然各截面上目标轮廓大体相似，但每层截面上目标轮廓存在位置偏差，需调整各轮廓曲线的位置，完全包括待分割目标。移动Bézier曲线的控制顶点调整此前生成的Bézier轮廓曲线族到待分割区域，如图12所示。

图12 Bézier曲线族调整图

为了满足体分割中空间封闭的条件，需要得到各轮廓曲线上所有的点在空间中的位置坐标以此来构造空间封闭轮廓曲面。但由于在反求Bézier曲线上点坐标存在着一定的困难和计算量较大等因素，现简化为通过对每条Bézier轮廓曲线上各控制顶点进行DDA插值的方法来得到近似的轮廓曲线上各点在空间中的位置坐标。

将得到的每条轮廓线上的点按照下述方法构造成空间封闭轮廓曲面。

（1）设定垂直于关键层面的轴向的正负方向，对轮廓曲线族中各轮廓曲线进行编号，使各轮廓曲线编号沿轴向正向依次增加；对每条轮廓曲线上的点沿着逆时针方向进行编号。

（2）从第一层轮廓曲线开始，沿点序号递增方向，取当前轮廓曲线中相邻的两个轮廓点、以及上层轮廓曲线中与点的编号相同的轮廓点。将、、三点连成封闭三角形。取与点同层且点序号增加1的点，将、、三点连成封闭三角形。

（3）依次类推，直到循环到最上面一层轮廓曲线终止。

根据封闭的轮廓曲面对待分割目标数据进行轮廓曲面内外标定，本文将轮廓曲面外的体数据点的灰度值置为-3000。

如图13所示为根据调整后的轮廓曲线族构造的轮廓曲面以及区域内外判断。

图13 轮廓曲面构造图

4 扫描线种子填充思想

体素是基本图元，是组成体数据的基本单位。体素又分为表面体素和内部体素。如果定义一个至少与其他体素6邻接或位于体数据边缘的体素为其表面体素，那么其表面体素可以组成一个18连通的封闭表面，同时它也可以表示为内部体素6连通的物体。

扫描线种子填充思想正是根据内部体素的6连通属性，从未被填充邻居区域中，选择新的种子，利用递归函数来实现。由于体数据的数据量大，而且递归函数在实现时要消耗大量的内存空间和花费大量时间。1985年Fishkin和Basky 通过分配给较短的像素跨度较高的优先级的方法提高效率。1995年Albert等为了减少内存的消耗和改善效率，提出了沿着某个方向连续填充体素的方法来代替仅仅填充相邻的一个体素的方法。1998年Feng和Soon从4邻域跨度并沿着一定的方向和堆叠一个或者多个新种子来填充一个跨度的体素。

但以上方法依然有两个缺点。首先，即使只有一个种子需要填充，但是不止一个的同样跨度的种子会被压入堆栈。其次，即使填充的区域没有包含新的种子点，但是寻找种子过程依然会在填充和未被填充的区域中执行的。

为了避免以上两个问题的发生，本文使用改进后的三维种子填充算法来实现分割。

对填充的过程进行记录就可以阻止多余种子的填充。即在寻找新种子点之前，需要比较相邻行和当前填充跨度的范围，之后根据比较的结果，判断是否进行新种子寻找。

相邻行与当前填充跨度的范围的比较可以被分作下述5种情况，如图14所示：

第1种情况 没有相邻的跨度与当前正在填充的跨度重叠。那么在相邻行的范围内寻找新的种子。

第2种情况 相邻的跨度包含了当前正在填充的跨度。不需要寻找新的种子点。

第3种情况 相邻的跨度的左半部份与当前正在填充的跨度相重叠。那么仅仅需要在相邻的跨度的右半部分寻找新的种子点。

第4种情况 相邻的跨度的右半部分与当前正在填充的跨度相重叠。那么仅仅需要在相邻的跨度的左半部份寻找新的种子点。

第5种情况 相邻的跨度完全包含在当前正在填充的跨度中。那么仅仅需要在没有重叠的相邻的跨度内寻找新的种子点。

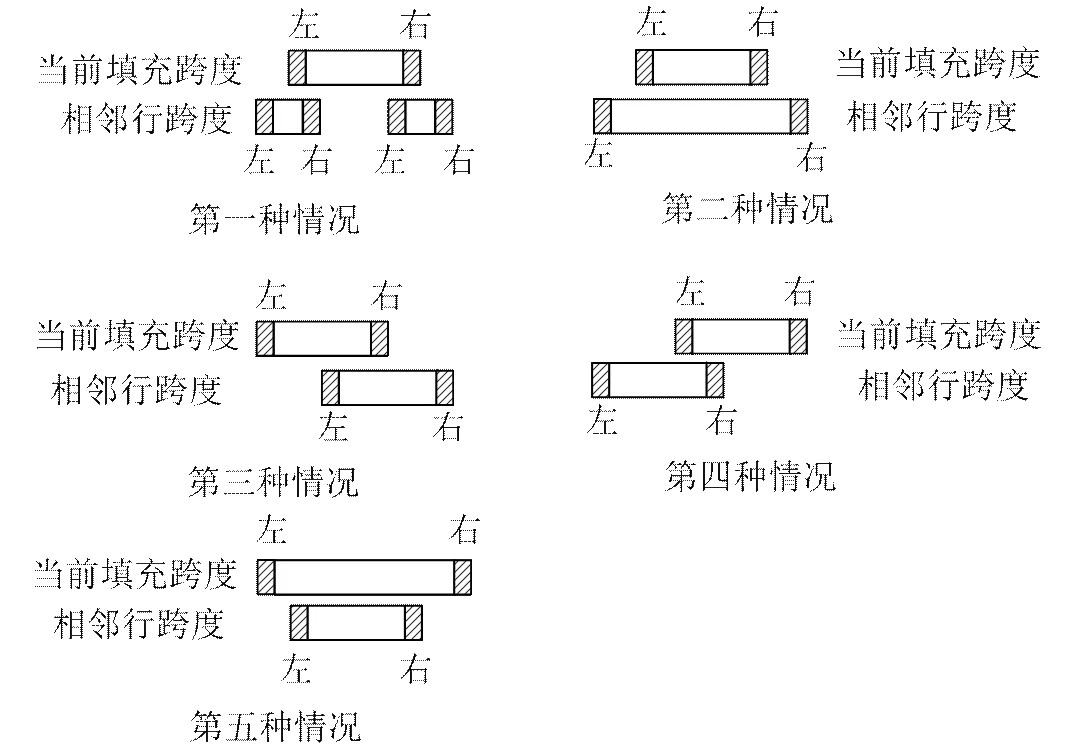
图14 相邻行与当前填充跨度范围比较分类图

5 实验结果分析

本文在INTEL的酷睿2双核1.66G，2G内存笔记本上进行三维分割算法实验，实验数据为Ⅰ:512×512×24和Ⅱ:512×512×57的两组CT切片图像。图15为Ⅰ、Ⅱ组图像的未分割组织图，图16为对两组数据使用Level Set算法三维分割结果，图17为本文算法三维分割结果。

(Ⅰ)      (Ⅱ)

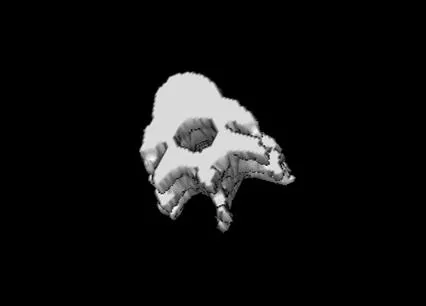
(Ⅰ)      (Ⅱ)

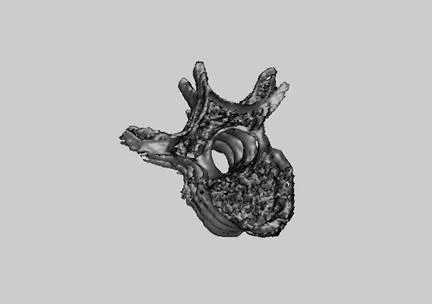
(Ⅰ)      (Ⅱ)

表1为本文算法和Level Set算法分割的比较结果。可比参数为分割时间。

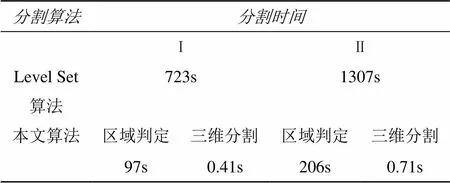
表1 本文算法与Level Set算法三维分割结果比较

由于三维种子填充算法存在回溯性，所以仅使用三维种子填充算法不能进行相连通部分的分割，否则会出现欠分割的情况。本文算法对（Ⅰ）组数据的三维分割时间是利用Level Set算法三维分割的时间13.4%，对（Ⅱ）组数据的三维分割时间是利用Level Set算法三维分割的时间15.8%，大大提高了分割效率。

6 总 结

本文提出一种新型的医学图像分割算法。该算法第一，利用Level Set算法对关键层图像（该层图像具有一组医学图像中与待分割组织的轮廓大体相似的特性）进行分割；第二，通过轮廓追踪得到分割后的关键层的外轮廓点，但由于在轮廓追踪过程中，目标轮廓的每一个像素点都被存储，造成数据冗余，不利于进行轮廓曲线投影后的轮廓调节。所以对轮廓点使用“弦差法”进行轮廓精简；第三，将轮廓点作为控制顶点生成Bézier曲线作为新的轮廓线；第四，将Bézier轮廓曲线进行投影，得到一族轮廓曲线；第五，调整每条轮廓曲线上的控制顶点使其达到恰当位置，利用DDA对调整到位的控制顶点进行插值，生成新的封闭的轮廓边界，利用轮廓曲线族构造轮廓曲面；第六，在封闭的轮廓边界内运用扫面线种子填充思想进行三维分割；最后完成分割任务。

[1] KASS M, WITKIN A, TERZOPOULOS D. Snakes: active contour models [J]. International Journal of Computer Vision, 1987, 1(4): 321-331.

[2] Malladi R, Sethian J A, Vemuri B. Shape modeling with front propagation: a level set approach [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1995, 17(2): 158-174.

[3] Sethian J A. A fast marching level set method for monotonically advancing fronts [C]//Proceedings of the National Academy of Sciences, 1996: 9389-9392.

[4] 张海波. 医学CT图像的三维分割与可视化研究[D]. 济南: 山东师范大学, 2005.

[5] Feng L, Soon S H. An effective 3D seed fill algorithm [J]. Comput Graph, 1998, 22(5): 641-644.

[6] 郭开波, 周 钢. 一种基于断层测量图片的实体轮廓提取算法[J]. 计算机辅助工程, 2001, (4): 50-54.

[7] 施法中. 计算机辅助几何设计与非均匀有理B样条[M]. 北京: 高等教育出版社, 2001. 115-165.

The Three-Dimensional Fast Segmentation Algorithm Based on Level Set Method

SUN Hai-peng, YU Wei-wei, XI Ping

( School of Mechanical Engineering and Automation, Beijing University of Aeronautics and Astronautics, Beijing 100191, China )

Because of the large volume of medical image data, the impact of noise, blurred boundaries and other reasons, the three-dimensional segmentation process is time-consuming, and easily produces less or over segmentation. To solve the above problems, this paper proposes a three-dimensional fast segmentation algorithm based on Level Set, using Level Set Fast Marching Method to obtain two-dimensional segmental region, optimizing the boundary contour, using the Digital Differential Analyzer method to extract contour pixels, finally introducing the idea of the Scan Line Seed-filling to achieve the three-dimensional fast segmentation. The actual clinical CT images of vertebral segmentation experiment result shows that this method can quickly and accurately separate out the interested area.

computer application;three-dimensional medical image segmentation; Level Set method; DDA; scan line seed-filling

TP 391.41

A

1003-0158(2011)03-0045-07

2009-11-02

孙海鹏（1985-），男，内蒙古多伦人，硕士研究生，主要研究方向为计算机可视化、医学图像处理。