基于突变理论的机场选址评价研究

李明捷，石 荣

（中国民航飞行学院a.空中交通管理学院；b.飞行技术学院，四川 广汉 618307）

机场选址作为机场总体规划的重要组成部分，既要满足功能性要求，同时又要满足经济和环境保护的要求。由于机场工程的复杂性，选址方案通常经过可行性研究、场址初选和场址定点等几个阶段多次反复、多个方面比较评价才能确定。在机场选址各阶段的方案比较评价中，通常采用专家决策法，即针对某项拟建工程项目，召集一批在该行业从事数十年研究的有关专家，跟据一些评价指标列出各方案的优点和缺点，然后进行商讨、比较和评价，在此基础上确定出一个最佳方案[1]。近些年，一些专家学者采用定量化方法对机场选址选择合理性评价进行了研究，蔡良才等利用层次分析法结合专家系统技术来对机场选址方案进行评价，但并未给出详细的评价指标体系[1]。孙志强采用评分优选法作为机场场址选择的定量优化方法[2]。戴福青等在使枢纽机场建设成本、航线网络上的飞行成本与航线扩容总成本之和最小化的基础上进行了单枢纽机场选址与航线网络规划的综合优化方法研究[3]。丁德亮等对机场选址考虑的影响因素进行了归类和分析[4]。李婷婷和高金华运用模糊多属性群决策方法机场选址评价问题进行分析[5]。杨青等以项目利益相关者价值最大化为目标，采用价值工程分析方法评价了首都第二国际机场项目四个潜在的新机场选址方案，从中得到了价值最优的场址方案[6]。张韬等人运用模糊相似优先比决策法对几个野战机场选址方案进行了决策排序[7]。

上述方法或模型主要是定性或者定性与定量相结合的评价方法。定性的方法对机场选址影响因素无法进行量化的、动态描述[4]，虽然定量的方法可以对影响因素进行量化及动态描述，但其前提是要对各个影响因素进行权重确定，而权重确定大都采用层次分析法，因而难免带有主观色彩，且计算过程复杂。突变评价方法是以突变理论为基础的评价方法，其突出的优点就在于通过指标之间的内在逻辑关系对指标的重要程度进行排序，无需人们确定指标因素的权重，可以减少主观性对评价结果的影响，且计算较为简捷。本文考虑将突变评价法应用于机场选址优劣评价，且对突变评价法中存在的突变评价值偏高的问题进行改进，使评价结果更具实用性。

1 突变评价法的基本原理

突变理论及突变评价方法的定义见文献[8]，其主要步骤如下：

步骤1：通过对影响机场选址主要因素的归类及分析，建立机场选址合理性评价指标体系。

步骤2：将突变理论与模糊数学相结合，对评价指标体系的最底层指标进行赋值，即根据各个底层指标因素的实际情况给出其模糊隶属度值。指标一般分为两类，一类是定性指标；一类是定量指标。对于第一类指标的可以采取专家打分法确定（一般是0～1之间的一个数值，数值越大表示该项指标对机场选址优劣影响越大）；第二类指标可运用级差变换法，将其进行标准化，处理为[0，1]之间的无量纲数值，指标值越大表示该项指标对机场选址优劣影响越大，具体做法如下：

对于指标越大越好型，可用下式进行计算

对于指标越小越好型，可用下式进行计算

式中：yi表示级差变换后的数据；xi为原始数据；max xi为xi中数据最大值；min xi为x中数据中最小值，i=1，2，…，n（n 为评价对象数）。

步骤3：利用归一化公式进行综合量化递归运算，并且根据“互补”和“非互补”原则逐层计算出指标因素的量值。常用的突变模型的归一公式有尖点突变模型、燕尾突变模型及蝴蝶突变模型的具体公式表达及模型示意图见文献[8]。

“互补”原则是指若同一个系统中各个控制变量间存在着明显的相互作用时，即按照指标数量的多少，根据其对应的突变模型归一化公式，取其隶属度值的平均数值作为状态变量X的值。而“非互补”原则是指若同一个系统中的各个控制变量之间不存在明显的相互作用时，则按照指标数量的多少，根据其对应的突变模型归一化公式，应采用“大中取小”，即取变量中值最小的一个作为整个系统状态变量X的值。

步骤4：对计算的结果进行改进，使之更具有实用价值。

2 突变评价法在机场选址评价中的应用

2.1 确定评价系统的指标体系

合理的机场选址必须使得机场净空、空域及气象条件能够满足机场安全运行要求，与邻近机场无矛盾或能够协调解决，与城市距离适中，机场运行和发展与城市规划发展相协调；场地能够满足机场近期建设和远期发展的需要，工程地质、水文地质条件良好，地形、地貌较简单，满足机场工程的建设要求和安全运行要求；具备建设机场导航、供油、供电、供水、供气、通信、道路、排水等设施、系统的条件；满足文物保护及环境保护等要求；占用良田耕地少，拆迁量和工程量相对较小，工程投资经济合理[9]。根据上述要求，建立机场选址合理性评价指标体系，如表1所示，并对各层次指标按重要程度进行排序，指标排序的原理是根据指标之间的作用关系及该指标对机场选址评价结果影响的重要性，例如对于指标（A，B）机场选址的内部影响因素和外部影响因素，实际上，在机场选址中，机场选址的内部因素状况在机场选址评价中更重要些，因此根据突变理论的原理，指标A排在B的前面。由突变模型原理及指标之间的作用机理，可知：指标（A，B）、（A1，A2）和（B11，B12）属于突变模型 I，其中，指标（A，B）为互补型，指标（A1，A2）和（B11，B12）为非互补型；（A11，A12，A13）和（B31，B32，B33）属于突变模型 II，均为非互补型 ；（A21，A22，A23，A24）、（B21，B22，B23，B24）、（B41，B42，B43，B44）及（B1，B2，B3，B4）属于突变模型III，（B21，B22，B23，B24）指标因素之间存在相互作用的关系，因此属于互补型，（A21，A22，A23，A24）、（B41，B42，B43，B44）及（B1，B2，B3，B4）指标因素之间不存在明显的相互作用关系，属于非互补型。

表1 机场选址合理性评价指标体系Tab.1 Index system of rationality assessment for aviation airport

2.2 确定底层指标模糊隶属度值

根据突变评价法第2步，将获得的底层指标进行规格化。由于本文中涉及的指标均为定性指标，因此可以通过专家打分法来确定评价因素对方案选择的影响程度。假设某市拟新建一机场，有3个备选方案，请专家按照方案的优劣程度，给出5个等级，即“差”、“较差”、“一般”、“较好”、“好”，其模糊值可定义为（0.5，0.6，0.7，0.8，0.9），给出底层指标的模糊隶属度值如表2所示。

2.3 利用归一化公式计算机场选址合理性评价突变值

根据突变评价法步骤3的方法，计算机场选址合理性评价突变值。以方案1的数据为例，其具体计算过程如下：

同理，可计算出的方案2和方案3的突变评价值，X2=0.954 9，X3=0.963 6。

2.4 突变评价值的改进

突变评价法也存在一定的缺陷，这主要由突变评价法的归一化公式的特点造成。一般对于评价结果应该具有绝对的“优”、“劣”含义，但是突变评价法的最终评价结果并非如此，普遍存在突变评价值偏高的特点。例如，当底层指标经量化后都取0.1时，根据上面给出的指标体系，可以计算出该方案的突变评价值为0.787 6，若从数值上来看，则该方案的选址处于较好和好之间，但实际上，这个方案应该是被否决的，这就说明由突变评价法评价所得的最终值的大小仅是对底层指标赋值结果的一种数值反映并没有绝对的“优”或“劣”的含义，因而在实际运用中，还需要对该评价结果进行转化。

为解决该问题，借鉴文献[8]的思想，以表1所示的评价指标体系算出来的突变评价值y=（0.986 5，0.954 9，0.963 6），根据 y与 x对应关系为

表2 机场选址合理性评价指标模糊初始值Tab.2 Fuzzy values of bottom indicators of rationality assessment for Civil Aerodrome

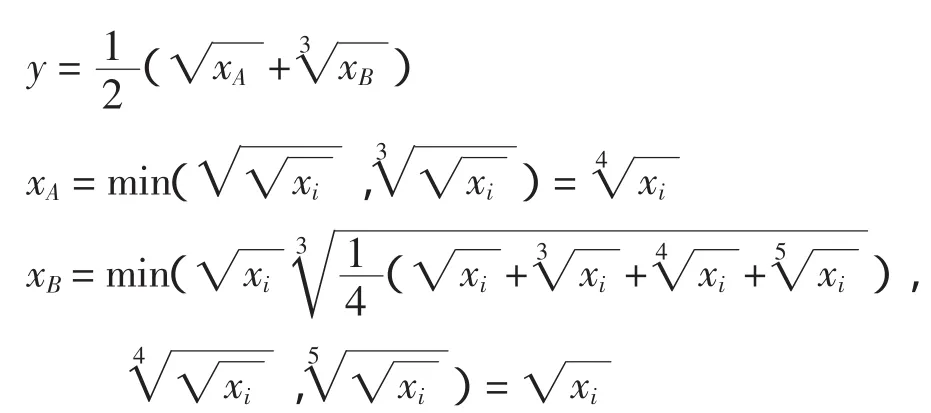
通过Matlab可以计算出y的变换值y变换=（x1，x2，x3）=（0.911 0，0.728 6，0.775 4），可见变换后的数值更接近绝对意义的“优”、“劣”概念，这使得突变评价法在评价工作用更加实用。根据上述评价结果可知，机场选址方案1评价值最高，因此，方案1建议为最佳方案。

3 结语

本文将突变理论引用到机场选址评价中来，通过定性分析建立分层次的机场选址评价指标体系，在给底层指标进行赋值时，仅考虑评估指标的相对重要性，避免了直接使用带有较大主观性的“权重”赋值。针对突变评价方法本身固有的评价值偏高问题，采用改进方法对其进行变换，增强了该评价方法的科学性与合理性。

[1]蔡良才，张晓义，邓学钧.机场选址方案综合评价智能辅助决策系统[J].航空计算技术，1996（3）:42-46.

[2]孙志强.民用航空机场场址选择概论[J].机场建设，2000（3）：19-20.

[3]戴福青，王 瑞.单枢纽机场选址与航线网络规划综合优化[J].中国民航大学学报，2000，25（1）:17-19.

[4]丁德亮，郑汝海，邵 斌.关于机场选址的思考[J].山西建筑，2007，33（22）:27-28.

[5]李婷婷，高金华.基于模糊多属性群决策方法的机场选址问题[J].交通与计算机，2008，26（5）:26-29.

[6]杨 青，邱菀华.价值工程分析方法及其在机场项目中的应用[J].北京航空航天大学报（社会科学版），2006，19（3）:1-4.

[7]张 韬，李赞成，陈 磊.环境因素对战时野战机场开设影响的模糊分析[J].国防交通工程与技术，2007（1）:46-48.

[8]施玉群，刘亚莲.关于突变评价法几个问题的进一步研究[J].武汉工业大学学报，2003，36（4）:132-136.

[9]中国民用航空总局.民用机场建设管理规定[S].2004.