抗拔桩荷载—位移曲线的荷载传递法解析

奚笑舟，陈龙珠

(上海交通大学 船建学院 安全与防灾工程研究所，上海 200240)

荷载传递法自Seed和Reese(1957)提出后，由于其概念简单，应用方便，只需确定桩侧和桩端的荷载传递函数，经过简单运算即可得到单桩荷载—沉降关系式，因此受到工程技术人员的认同。近年来，学者们在抗拔桩的研究中也引入了荷载传递法，取得了不错的效果［2-3］。对于桩侧土的荷载传递函数，很多研究表明，双曲线型的传递函数能够较好地模拟桩土间的荷载传递特性[4]。由于双曲线型的传递函数会带来微分方程求解上的困难，所以一些学者用折线来对其进行简化，如陈龙珠等[5]提出的双折线模型、刘杰等[6]提出的三折线软化模型等。本文采用三折线弹性—应变硬化—理想塑性荷载传递函数来分析抗拔桩的荷载传递规律，建立了一种适合于层状地基中抗拔桩的轴向荷载—位移关系曲线的非线性解析算式，并利用既有文献中的原型试验数据来进行拟合分析，以此检验该方法的可行性。

1 抗拔桩荷载—位移曲线解析算法公式推导

1.1 荷载传递法基本微分方程

在抗拔桩中，桩身受力为拉力，其荷载传递法的桩土计算模型如图1所示，桩侧摩阻力与桩端阻力均用非线性弹簧表示，桩身轴力以拉力为正。由于桩身自重与桩顶加载方向相反，所以在解析中需考虑桩身自重的影响。

根据图1中桩微段的Z向静力平衡，可以得到桩身轴力Q(z)、材料重度γ(在地下水位以下取有效重度)、桩身截面积A和周长u、桩身截面位移 W和侧摩阻力qs之间的关系为

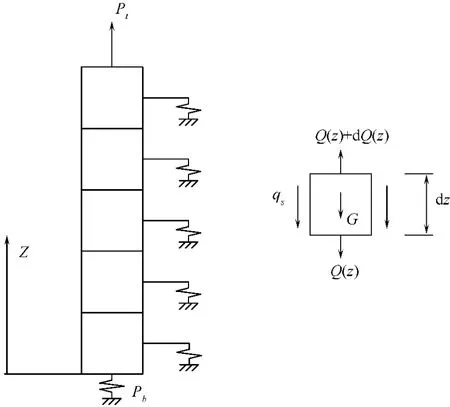
图1 抗拔桩桩土计算模型

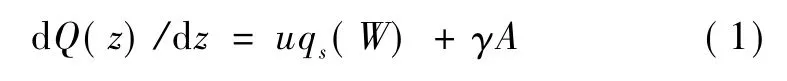
将桩视为等截面弹性杆件，由桩身线弹性应力应变关系，E为桩身弹性模量，得

由以上两式可以得到抗拔桩的荷载传递法基本微分方程为

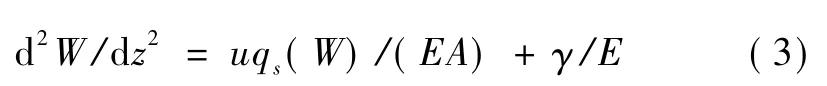
其中，桩侧摩阻力qs是桩身位移W的函数，也即荷载传递函数。选择适合的荷载传递函数qs代入基本微分方程并求解，即可得到桩中的轴力、侧摩阻力、桩身沉降等情况。由于抗拔桩中的轴力为拉力，而土的抗拉能力很弱，所以桩底轴力Pb为拉力时可视为0。

1.2 桩侧土的荷载传递函数

很多研究表明，桩侧土具有很强的非线性，曹汉志[7]通过对华南地区试桩结果的研究，认为桩侧土一般为非线弹性—理想塑性型，所以本文将桩侧土简化为图2所示的三折线弹性—应变硬化—理想塑性模型。这样的简化可以保留最大侧摩阻力、分界位移的物理意义，在加载的开始阶段由初始剪切刚度控制，用双折线来模拟桩侧土的非线性，提高了非线性阶段的拟合精度，可表达为

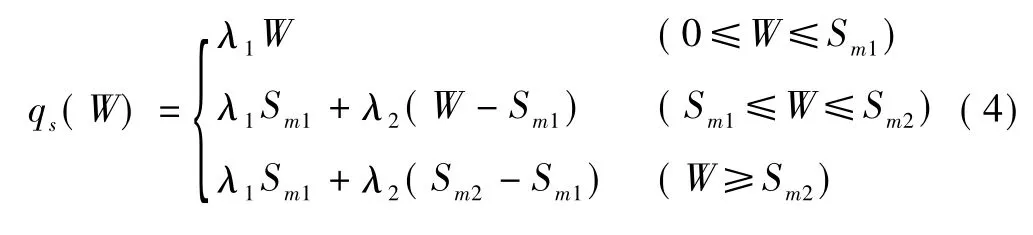
式中，Sm1为弹性阶段的极限位移，Sm2是达到最大侧摩阻力时需要的桩身位移，也是塑性硬化段的极限位移;λ1，λ2分别为弹性和硬化阶段的抗剪刚度系数。对于具有明显应变软化阶段的土，诸如疏松砂土、部分嵌岩桩中的桩侧摩阻力，可以令λ2＜0，即可转化为应变软化型荷载传递函数。

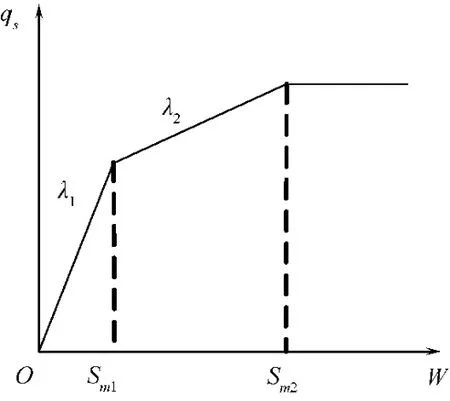
图2 桩侧土三折线传递函数模型

1.3 解析推导

假定抗拔桩侧为单层均质地基土，桩为等直截面线弹性杆。当在桩顶施加上拔荷载，桩侧土在桩顶处随着荷载的增加，将先于下部土从弹性状态进入塑性硬化状态;荷载继续增加，上部土进入理想塑性状态。桩下部桩身位移小于上部桩，下部土的状态转化要迟于上部土。当桩侧土全部进入理想塑性状态后，可以认为达到了抗拔桩的极限承载力。

如图3所示建立坐标系，以桩端为原点，向上为正，桩身轴力以拉力为正。抗拔桩桩长L，记R1，R2，R3为桩侧土分别处于弹性、应变硬化、理想塑性阶段的长度，则有L=R1+R2+R3。桩端轴力和位移用(Pb，Sb)表示，桩顶轴力和位移为(Pt，S)，Pt即为上拔荷载。以(Pb，Sb)作为边界条件，通过比较 Sb与桩侧荷载传递函数各阶段的极限位移Sm1，Sm2，可以通过假设桩侧土状态来得到相应的桩顶轴力和位移(Pt，S)，其中符合假设的结果即为实际解。

在解析中，各参数定义为

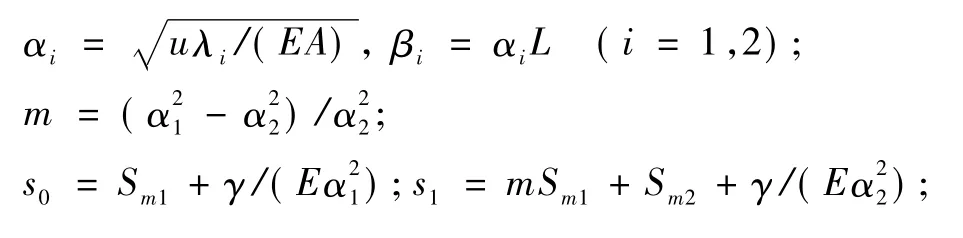
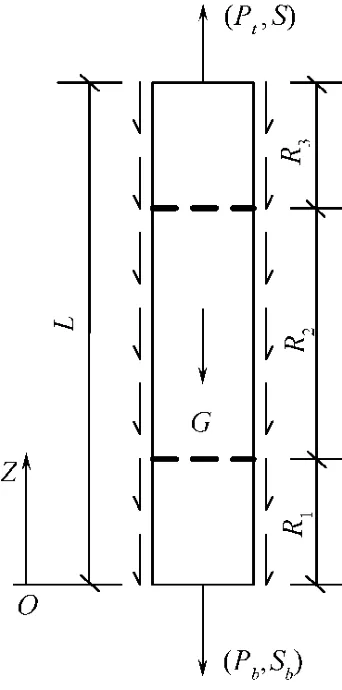
图3 抗拔桩桩侧土分别处于不同阶段

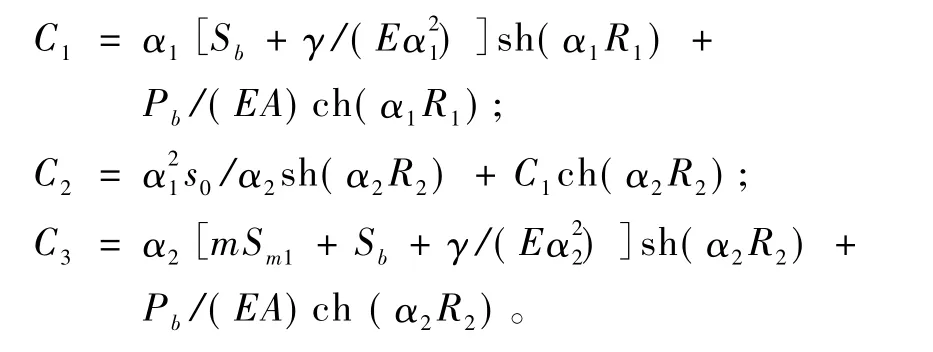
求解过程不再赘述，结果记述如下所述。

1)如Sb＜Sm1

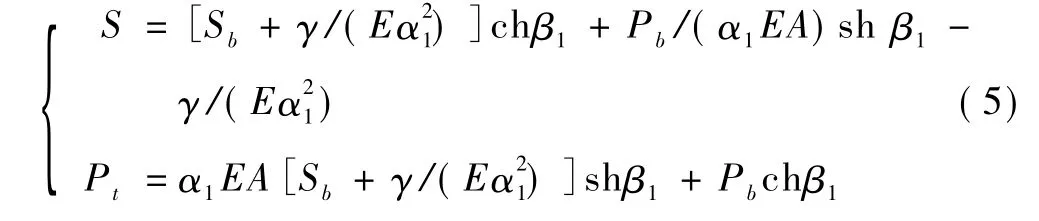
①假设桩侧土均为弹性状态(R1=L，S≤Sm1)。②桩侧土部分弹性，部分塑性硬化(R1+R2=L，Sm1＜S≤Sm2)。R1由式(6)求解。

③桩侧土中同时存在弹性、应变硬化和理想塑性状态(R1+R2+R3=L，S＞Sm2)。其中 R1由式(6)求解，R2由式(8)求解。

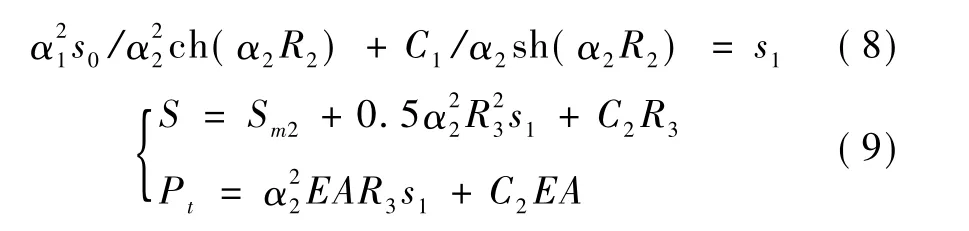
2)如 Sm1≤Sb＜Sm2

①桩侧均为塑性硬化(R2=L，Sm1＜S≤Sm2)。

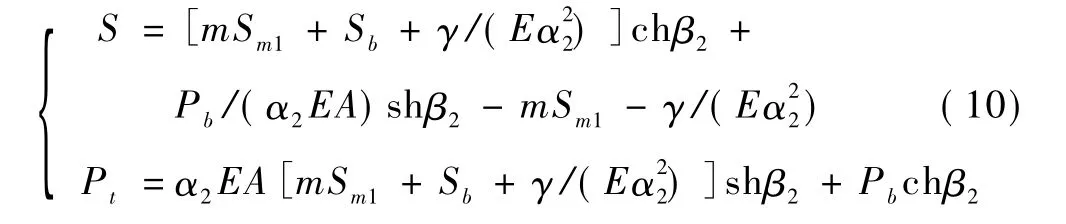
②桩侧部分塑性硬化，部分理想塑性(R2+R3=L，S＞Sm2)。R2由式(11)求解。

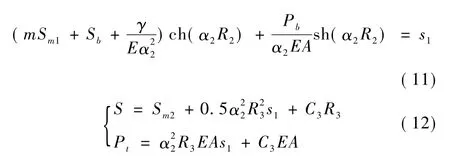
3)如Sb≥Sm2，此时桩侧土全部处于理想塑性状态(R3=L，S ＞ Sm2)。

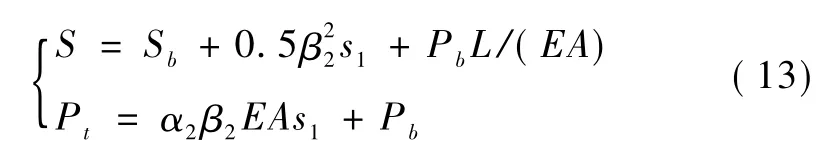
假设抗拔桩侧土为均质单层，当桩底产生一个向上的位移Sb时，由于土的抗拉能力可以忽略，则认为桩端土与桩端脱开，即有Pb=0。所以可以假设一个较小的桩端向上位移 Sb，令 Pb=0，代入以上方程，求得符合假设的解作为桩顶轴力和位移;逐渐加大Sb，重复求解过程，则可以得到一系列桩顶轴力和位移，即为桩顶上拔荷载—位移理论曲线。

对于成层地基中的抗拔桩，可将桩身按桩侧土的性质以及桩身截面的变化划分为若干个计算段，对每个桩段按均质地基的方法计算。其中令桩端处计算段的桩端轴力Pb=0，计算得到该段桩顶截面的轴力和位移，并以之作为上一段底截面的轴力和位移边界，代入以上解析求解;以此方法从桩端开始向上逐段计算，直到求得桩顶处的轴力和位移，即为成层地基中抗拔桩的荷载—位移曲线即Pt—S。

2 拟合方法与参数确定

从以上的解析中可以看出，理论Pt—S曲线是由直线段(桩侧土全部处于弹性、塑性、理想塑性阶段)以及之间连接的曲线段(桩侧土中存在不同的荷载传递阶段)组成。因此，对于均质地基，可以通过对实测曲线的直接拟合得到荷载传递函数的参数。而对于成层地基，需要首先估计传递函数的参数初值，再逐渐调整参数，使理论曲线与实测数据吻合来得到较准确的结果。

当前抗拔桩的摩阻力确定主要是以桩的抗压侧摩阻力乘以抗拔系数得到，我国桩基规范(JGJ 94—2008)[1]推荐的抗拔系数为:砂土 0.5 ～0.7，黏土、粉土0.7～0.8，其中桩长径比＜20时取低值。这里对抗拔侧摩阻力的折减程度较大，是偏于安全的。在传递函数参数的确定中也可以采用这种方法。下面简述层状地基中的拟合方法。

1)根据桩侧土的性质和桩身截面的变化将抗拔桩划分为若干个计算段。

2)确定各计算段土层的抗拔最大侧摩阻力 qu。抗拔最大侧摩阻力可以根据地质勘探资料或由当地经验获得，也可以先估计抗压最大侧摩阻力，再乘以抗拔系数得到。抗压最大侧摩阻力的取值主要有 α法、β法、λ法等，在此不再赘述。

3)确定各计算段土层的初始抗剪刚度系数 λ0。初始抗剪刚度系数的取值也可以借鉴抗压桩的相关研究成果，如 RANDOLPH 和 WROTH(1978)[8]认为对均匀各向同性、弹性土中的桩可以用以下公式计算

其中，G0为土的初始剪切模量;r0为桩身半径;rm为剪切影响半径，可由rm=2.5Lρ(1－ν)求得，如考虑土中剪切模量随深度的变化，则ρ=G(L/2)/G(L)，即土中剪切模量在桩长一半处与桩底处的比值，ν是桩周土的泊松比。ln(rm/r0)的值变化不大，一般在3～5之间，没有详细数据时可取4.0左右而不致引起很大误差。求得抗压桩初始抗剪刚度系数后，乘以抗拔系数作为抗拔桩的取值。

4)Sm2可以认为是桩侧摩阻力达到最大时的桩身截面位移，RAO(1985)认为松砂中桩达到极限承载力时，抗拔桩对应位移大约为桩径的5%;而在密砂中桩达到极限承载力的对应位移大约为桩径的10%。由以上解析可以看到，抗拔桩荷载—位移曲线在开始阶段是直线，其终点为桩顶位移达到Sm1，所以Sm1可根据实测曲线的第一拐点确定。

5)令 λ1=λ0，由于 qu=λ1Sm1+λ2(Sm2－ Sm1)，所以可以由此估计λ2的取值。

6)根据以上方法确定各计算段的传递函数参数初值，将之带入求解，如与实测曲线不符，可固定各计算段中参数的相对比例，然后调整参数至与实测曲线吻合，即得到较为准确的解析解。如有轴力实测数据，可参考轴力数据进行调整。若计算段内含有多个土层，在确定传递函数初值时可取各土层的加权平均值。

3 算例

为了检验本文方法的有效性，这里对一个工程实例进行了分析。上海新梅莘苑地下车库位于上海市闵行区莘庄镇内，地下车库由于无上部荷载，采用抗拔桩基进行处理，进行了基桩竖向抗拔静载荷试验[9]。该工程自地表到80 m深度范围内所揭露的土层均形成于第四纪的全新世及晚更新世，主要由饱和的黏性土和砂性土组成，具有成层分布的特点。年平均水位埋深为0.5～0.7 m。试验场地各土层的物理力学性质见表1。

基桩采用预制混凝土方桩，采用锤击法施工，混凝土强度等级为 C30。桩的截面尺寸为250 mm×250 mm，工程桩桩长16 m，试桩桩长20 m，设计单桩竖向抗拔极限承载力标准值为275 kN。总桩数为170根，对其中3组基桩进行了竖向抗拔静载荷试验。试验采用锚桩反力法，本文选取其中的84#试桩进行分析。出于简化拟合过程的考虑，将性质相近的土层合并，作为同一层考虑，通过对实测数据的拟合，可以得到表2所示的传递函数参数。

表1 土层部分物理力学指标值

理论计算得到的曲线见图4。根据文献[9] 中的数据，第1、2个计算段的最大侧摩阻力在 10 kPa左右，而第3、4个计算段在25 kPa左右，所以可以预计，第3、4个计算段中的土将很快达到最大侧摩阻力，而第1、2个计算段中的土还需要更大的位移才能达到最大侧摩阻力。图4(a)中为理论Pt—S曲线与实测数据，可见两者的吻合度较高，且可预计，如继续加载，曲线将很快出现向上的明显弯曲。由于第3、4两个计算段达到最大侧摩阻力后，Pt—S曲线斜率已经很大，所以可以认为，此时已经达到桩的最大抗拔承载力，大致为380 kN，满足设计要求。图4(b)、图4(c)为在各级荷载下，桩身轴力和侧摩阻力沿桩长的分布，其中轴力分布曲线的斜率可反映桩侧土对侧摩阻力的贡献。

表2 传递函数拟合参数

图4 84#试桩实测曲线与解析解

4 总结

本文对抗拔桩侧土的荷载传递函数采用三折线模型，推导出了能确定层状地基中抗拔桩桩顶荷载—位移关系曲线，各级荷载下桩身轴力以及侧摩阻力沿桩长的分布的解析算式。与既有文献的试验数据的比较分析初步表明，在参数选取符合场地地质条件的前提下，该方法能很好地用于抗拔桩荷载—位移曲线的拟合分析，从而为试验研究抗拔桩的工程力学性状和优化抗拔桩设计提供了一种较为简便实用的理论计算方法。

[1] 中华人民共和国建设部．JGJ 94—2008 建筑桩基技术规范［S］．北京:中国建筑工业出版社，2008．

[2] GOEL S，PATRA N R．Prediction of load displacement response of single piles under uplift load［J］．Geotechnical and Geological Engineering，2007，25(1):57-64．

[3] SHANKER K，BASUDHAR P K，PATRA N R．Uplift capacity of single piles:predictions and performance［J］．Geotechnical and Geological Engineering，2007，25(2):151-161．

[4] ALAWNEH A S．Modellingload-displacementresponseof driven piles in cohesionlesssoilsundertensileloading［J］．Computers and Geotechnics，2005，32(8):578-586．

[5] 陈龙珠，梁国钱，朱金颖，等．桩轴向荷载—沉降曲线的一种解析算法［J］．岩土工程学报，1994，16(6):30-38.

[6] 刘杰，张可能，肖宏斌．考虑桩侧土软化时单桩荷载—沉降关系的解析算法［J］．中国公路学报，2003，16(2):61-64.

[7] 曹汉志．桩的轴向荷载传递及荷载—沉降曲线的数值计算方法［J］．岩土工程学报，1986，8(6):37-49.

[8] RANDOLPH M F，WROTH C P．Analysis of deformation of vertically loaded piles［J］．Journal of the Geotechnical Engineering Division，1978，104(12):1465-1488．

[9] 凌辉．上海软土中单桩抗拔承载机理研究［D］．上海:同济大学，2004.