基于PIC法SF6/N2混合气体中绝缘子沿面放电特性研究
汪 沨 肖晓林 张宪标 付婷婷 王 强 张贵新
(1. 湖南大学电气与信息工程学院 长沙 410082 2. 清华大学电力系统及发电设备控制与仿真国家重点实验室 北京 100084)
1 引言
SF6/N2混合气体放电特性仿真,对于进一步理解其放电机理,推进新型气体绝缘方式的 GIS绝缘设计方面具有重要意义。目前,一些研究者采用了基于流注放电理论的流体模型,比如澳大利亚科学家Morrow对 SF6气体流注放电进行了流体动力学模拟;德国达姆施塔特工业大学的 Pfeiffer研究了SF6/N2混合气体的流注放电机理;剑桥大学Georghiou、Metaxas与Morrow合作完成了空气间隙的二维流体动力学模型的模拟[1-4]。但以上研究方法是从宏观的角度将流注放电发展的动态行为假设为大量带电粒子的流体运动,并不是针对单个带电粒子的运动及粒子间的碰撞电离过程,无法模拟出实际放电过程中各带电粒子间的非线性作用过程,并且流体模型对于纯气隙的放电模拟比较便捷,对于绝缘子沿面放电行为的仿真将非常困难。而Dawson等人于1960年左右创立的等离子体的粒子模拟方法是通过计算大量单个微观粒子的运动[5],得到宏观物体的物质特性和运动规律,反映实际带电粒子的运动,并可得到任何详细的等离子体运动的信息。所以针对目前的研究现状,采用等离子体粒子模拟方法(Particle-in-Cell Method, PIC法)模型研究SF6/N2混合气体放电更接近于实际情况。
国内一些研究所和高校曾针对自由电子激光、激光等离子体波电子加速器、虚阴极振荡、强激光与等离子体相互作用等问题进行粒子模拟[6-13],并且一些院校也做到了二维激光等离子体模拟,如北京大学的电子工程学院做了在单一氢气短间隙场域PIC仿真[6],上海交通大学肖登明教授课题组采用改进的蒙特卡罗算法对 SF6及 CO2电子崩参数进行了仿真[7]。而对于 SF6/N2混合气体放电的 PIC仿真报道不多。国外的科研机构和院校研究的气体放电PIC仿真大多是在真空或其他气体(Ar、He),美国密苏里哥伦比亚大学做了激光触发火花间隙放电 PIC仿真[8]。本文在前人的研究基础之上,采用PIC模型对10%~90% SF6/N2混合气体放电过程进行仿真。
2 蒙特卡罗碰撞模型及PIC算法
2.1 蒙特卡罗碰撞电离模型
蒙特卡罗方法(Monte Carlo Method),也称统计模拟方法,是20世纪40年代中期由于科学技术的发展和电子计算机的发明,而被提出的一种以概率统计理论为指导的一类非常重要的数值计算方法[14]。
英国开尔文于 20世纪初曾记录他的助手对一组标了数的卡片抽样选取的随机数,来计算分子与壁面的碰撞。这是用统计试验法对气体行为所作的最早模拟。20世纪40年代,Ulam和Von Newmam首先用这种方法计算中子链式反应,后来Fermi又用这个方法计算扩散问题。美国橡树岭实验室从20世纪 60年代开始研制的大型多功能多群中子光子耦合输运蒙特卡罗方法计算程序,它广泛地用于核辐射屏蔽问题,该程序从1970年投入使用,经过多次修改和补充,至今已形成具有特殊功能和使用价值的版本。20世纪70年代末,Buffon提出的用随机投针实验求值的尝试,使蒙特卡罗方法迅速进入求解方程根的领域。20世纪80年代后,随着计算机的普及,蒙特卡罗方法涉及计算物理各个领域,得到了更新更广泛的应用。近几年,在射线成像系统的研究、核辐射屏蔽问题计算、中性粒子输运和分布问题计算、高分子链的相关参数计算、混合物的相图模拟、低能电子散射问题以及动态系统可靠性仿真问题等较前沿的研究中,蒙特卡罗方法用得很多,并且得到了经济可靠的结果。蒙特卡罗方法的随机抽样理论对物理现象的研究计算,尤其对微观物理学前沿研究领域非常适合,提供了不可代替的计算手段[15]。
等离子体粒子模拟(PIC)的基本思路是:先设大量的带电粒子具有初始位置和速度,对它们统计平均求出等离子体空间的电荷密度分布,再通过泊松方程求出各处的电场,这样,可得出每个粒子所受的力,而下一时刻每个粒子的位置和速度可以通过运动方程求出。如此循环进行,跟踪计算大量带电粒子的运动。
本文用于模拟SF6/N2混合气体放电动态过程的碰撞类型包括:
六氟化硫气体

氮气

气体中的粒子处于不规则运动,不断相互碰撞。粒子间相继两次碰撞之间的平均距离称为平均自由程。通过平均自由程模型可求解出粒子碰撞后的位置。
在电场中电子沿抛物线轨迹运动直到与气体分子发生碰撞,平均自由行程λ为

单位时间步长Δt内电子与气体分子发生的碰撞概率Pj为

蒙特卡罗碰撞模型的中碰撞截面的含义为粒子半径和粒子之间相互作用的几率,即假设在碰撞过程中,投射粒子流电子流的密度N0为 1,即 1s内通过1cm2面积的电子数为1,那么电子受到碰撞的几率表示为靶粒子的截面积σ除以1cm2。
对于各种碰撞过程可以用不同的有效碰撞截面去描述,如弹性碰撞截面、激励碰撞截面、电离碰撞截面和附着截面等。
确定碰撞类型时,首先需要确定电子和哪种气体分子发生碰撞。在假定气体分子密度不大,分子之间不存在化学作用,而仅发生随机碰撞的条件下,按照统计物理的观点可以首先确定电子和每种分子的碰撞概率,再确定电子和某种分子发生的碰撞类型概率。
以 SF6、N2气体分子为例,其分子密度分别为N1、N2,则气体的电子碰撞宏观总截面为
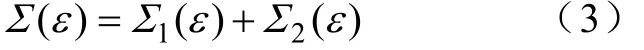
式中,ε为电子的动能;Σ1、Σ2分别为 SF6、N2总截面。其定义如下:

由于电子碰撞截面表示电子与分子发生碰撞可能性的大小,因此与 SF6、N2分子发生碰撞的概率P1,P2分别为

令

可以推出

电子与某种气体分子碰撞可以发生多种碰撞如弹性散射,激励碰撞以及附着等。设σel、σex、σion和σa分别为弹性碰撞截面、激励截面、电离截面和附着截面。
因此发生激励碰撞、电离碰撞及吸附碰撞概率的概率分别为
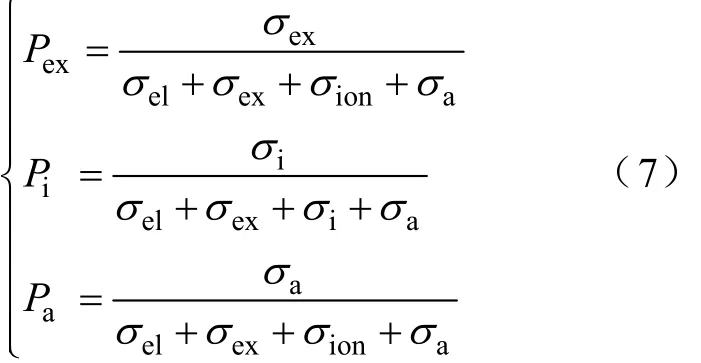
本文用于仿真放电过程的碰撞截面分别为:
(1)SF6电离碰撞截面
电离的临界能量εcr为15.8eV,其拟合表达式为

式中,εi,j分别为 15.8eV、21.5eV、34eV、50eV;Dj分别为 1.02、1.11、1.35 和 1.35;βj分别为 1.0、2.5、2.5 和 2.5。E(ε)分别为 0.0、3.92、27.0 和0.28ε+13.0(10–17cm2)。

否则,qi,1=0。
(2)SF6吸附碰撞截面
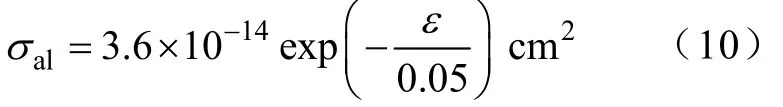

③F-的碰撞截面为

(3)SF6激励碰撞截面
SF6的激励态可以分为 6组,其临界能量分别为 9.6、11.0、11.6、12.8、13.3和 18.0eV,其拟合表达式为

其中,εj= 9.6, 11.0, 11.6, 12.8, 13.3, 18.0 eV
qj= 0.924, 1.8, 1.8, 1.8, 2.28, 0.24 10-17cm2
αj= 6.0, 6.5, 6.0, 4.0, 2.0, 2.0
j= 1, 2, 3, 4, 5, 6

(4)SF6弹性碰撞截面

(5)N2电离碰撞截面

(6)N2弹性碰撞截面为离散数据,通过插值技术实现。
2.2 PIC法粒子模拟
放电空间的电荷分布直接决定电场的分布。在空间电荷区内,电场、电荷和电位之间的内在关系可由泊松方程描述为

式中,φ为电位分布;εD为介质介电常数;Np,Ne,Nn分别为正、电子、负离子的浓度;φ|L为电极电位。应用等参元方法把整体坐标系转化为单元格内的局部坐标系进行求解得出空间网格各个节点电位。再得出各个节点的电场强度。
由于粒子不一定在空间网格节点上,那么,对于每个单元格内粒子所处场强值可采用适当的插值或权重法进行求解。在这里采用一阶权重法(线性插值),也就是面积权重法,将空间网格节点上的值加权到粒子所在位置;在二维情况下三角网格为例,二维线性加权的电场分布如图1所示。图中,A、B、C为网格节点,O为带电粒子所在位置,S1、S2、S3为图中阴影部分的面积,粒子所处位置的电场强度为

式中,S=S1+S2+S3。

图1 二维线性加权的电场分布Fig.1 Field assignment for linear weighting
模拟用绝缘子为圆柱型绝缘子,采用聚四氟乙烯材料,夹在两平板电极之间,其直径为 32mm,高度为40mm;绝缘子内屏蔽电极的高度为20mm,直径为24mm,如图2所示。由于PIC法需要对大量带电粒子进行跟踪仿真,为提高效率,本文仅对p=1.0Torr(1Torr=133.322Pa)条件下的 SF6/N2的绝缘子沿面闪络问题进行研究。

图2 电极及绝缘子结构图Fig.2 Schematic configuration of electrode and insulator
粒子运动模拟过程中,假设第j个带电粒子在电场作用下运动,其动力学运动方程为
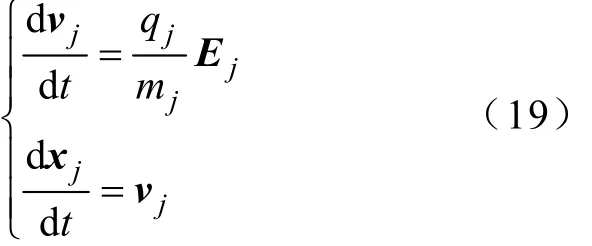
式中,vj为粒子运动速度;qj为电荷量;Ej为电场强度;mj为粒子的质量;xj为粒子运动的位移。
用时间中心差分方法将上式化为差分方程

整个计算过程采用一种蛙跳推进格式(leapfrog)推动粒子的运动,即已知(n-1)Δt时刻粒子的速度、(n-1/2)Δt时时刻粒子的位置和场强,可以得出nΔt处的速度、(n+1/2)Δt时刻粒子新的位置和场强,重复这一过程,即可实现对粒子的跟踪。

图3 蛙跳格式图Fig.3 Leap-frog scheme
采用上述蛙跳格式求解式(20)可得

式中,vj代表第j个电子的速度。这样就可以得出每隔Δt后的新速度和位移。
3 结果及讨论
3.1 电场计算
假定初始条件:绝缘子两电极间施加 500V直流电压,同时在负电极附近释放200个初始电子,通过电场的求解可以得出混合气体场域中电位分布图和电场强度矢量图,如图4所示。
从图中可以看出绝缘子内屏蔽电极较高,此时电场的法向场强会比较大,电子在绝缘子、电极和气体分界面处极易受法向场强影响运动到绝缘子表面,形成表面电荷积聚。选择这种电极结构对于研究表面电荷积聚机理及其对气体放电的影响具有明显的效果,并有利于提高本次绝缘子沿面放电模拟的效率。
3.2 放电发展

图4 电位分布图及电场矢量图Fig.4 Potential distribution and electric field vector
初始时刻(t=0)释放的N个初始电子在电场作用下向正极方向运动过程中,分别与 SF6、N2中性分子发生弹性碰撞、电离碰撞、激励、吸附等过程,不但有可能产生出正离子和电子,也有可能形成负离子。放电发展过程中产生的新电子 e、正离子和以及负离子、S、F-,在电场作用下的运动轨迹的仿真结果如图5所示,其中绝缘子及电极布置图同图2。

图5 电子崩的发展进程Fig.5 Electron avalanche development
气体放电一般是从电子碰撞电离开始发展到电子崩的阶段,从图5中可以看出在电子碰撞向前发展的前10ns内,阴极附近仍然有大量的电子存在,这是由于电子的逆扩散过程,慢慢地电子崩发展到t=20ns时,由于极性相斥的关系,电子向阴极的反方向运动,并在运动过程与 SF6、N2气体中性分子发生碰撞电离,产生出大量新电子。t=30ns时,由于受电场力影响,电子开始逐渐恢复到向绝缘子表面方向运动。到t=45ns时,大量电子在绝缘子表面形成积聚,由于表面电荷积聚会对电场产生影响,进一步畸变电场,加剧电子沿着绝缘子表面运动。所以到t=60ns时,电子的运动集中于绝缘子表面向前发展。
SF6/N2混合气体中,负离子的形成主要有以下几种途径:

电子被SF6气体分子捕获,发生附着过程。S、S、F-负离子分布的仿真结果如图6所示。

图6 负离子发展Fig.6 Negative ions development
SF6/N2混合气体中,正离子的形成途径如下:


图7 正离子发展Fig.7 The positive ions development
图6和图7中,由于SF6气体是一种强电负性气体,负离子的形成并未使带电粒子数增加,而是使自由电子数减少,对放电发展起抑制作用。并且可以看出、正离子和、S、F-负离子由于其荷质比q/m相比电子要大好几个数量级,所以在电场作用下运动速度和位移很小,其运动发展轨迹有明显的发散放电效果。其中正离子沿绝缘子表面发展的轨迹尤为明显。
3.3 电子崩电流
电子碰撞电离产生电流,由电流的定义:单位时间内通过横截面的电量,即I=q/t,可以转化为求解N个电子运动产生的电流。
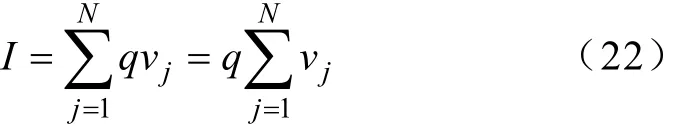
式中,vj代表第j个电子的速度。
气体放电过程中,大量带电粒子在电场作用下作定向运动,消失于电极上。带电粒子、位移电流、以及用于提供粒子运动、碰撞所必需消耗的微弱电流能量一起构成外回路电流。由于本文研究的是直流电压,因此可不计位移电流的影响。另外用于提供粒子运动及碰撞所耗电流很小,因此本文忽略了该部分电流。相对于电子来说正负离子运动范围较小,在放电最初时刻主要考虑电子运动产生的电子崩电流,通过式(20)求解可以进一步得到图8所示i-t特性曲线。图中,电流随着电子运动速度的提高、数目的增多而增大,当到达t=30ns时,电子数目略有下降,但由于场强畸变的缘故,电流会有所波动,但随着时间推进,电流趋于饱和,总体的走向会趋于稳定。

图8 电子崩电流Fig.8 Electron avalanch current along the axis
4 结论
利用等离子体运动学方程,通过粒子网格法对SF6/N2混合气体中绝缘子沿面放电过程进行仿真,研究其局部放电机理。通过二维泊松方程,应用有限元方法求解电场,采用蛙跳格式跟踪粒子的运动。采用蒙特卡罗碰撞(MCC)模型模拟粒子的碰撞过程,实现二维环境下SF6/N2混合气体放电过程动态仿真。
模拟过程中考虑了电子与 SF6、N2中性粒子的电离、吸附、复合以及光电离等过程。给出了不同时刻场域空间内部的电子、正、负离子的动态分布图。仿真结果首次清楚地展示了电子在电场力的作用下,运动到绝缘子表面产生表面电荷积聚的动态过程。
[1] Morrow R. Properties of streamers and streamer channels in SF6[J]. Phys. Rev. A, 1987, 35(4): 1778-1785.
[2] Vitello P A, Penetrante B M, Bardsley J N. Simulation of negative-streamer dynamics in nitrogen[J]. Phys.Rev. A, 1994, 49(6): 5547-5598.
[3] Pfeiffer W, Tong L, Schoen D. Computer simulation of streamer discharge processes in SF6and SF6/N2mixtures[C]. XIV International Conference on Gas Discharges and Their Applications, Liverpool, 2002:227-230.
[4] Georghiou G E, Morrow R, Metaxas A C. Twodimensional simulation of streamers using the FE-FCT algorithm[J]. Journal of Physics D: Applied Physics,2000, 33(3): L27-32.
[5] Dawson J M. Particle simulation of plasmas[J]. Rev.Mod. Phys., 1983, 55:403.
[6] Xiang W, Zhao W J, Dai J Y. Particle-in-cell simulations on a single gap gas discharge[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2003, 10(4):590-595.
[7] 吴变桃,肖登明. 用改进的蒙特卡罗法模拟 SF6和CO2混合气体电子崩参数[J]. 电工技术学报,2007,22(1): 13-16.
Wu Biantao, Xiao Dengming. An improved Monte-Carlo method for simulation of electron swarm parameters of SF6and CO2gas mixtures[J]. Transactions of China Electrotechnical Society, 2007, 22(1): 13-16.
[8] Worts Eric J, Kovaleski Scott D. Particle-in-cell model of a laser-triggered spark gap[J]. IEEE Transactions China on Plasma Science, 2006, 34(5): 1640-1645.
[9] Soria C, Pontiga F, Castellanos A. Particle-in-cell simulation of electrical gas discharges[J]. Journal of Computational Physics, 2001, 171(1): 47-78.
[10] Vahedi V, Surendra M. A Monte Carlo collision model for the particle-in-cell method: applications to argon and oxygen discharges[J]. Computer Physics Communications, 1995, 87(1): 179-198.
[11] Pfeiffer W, Feng Wang, Kouzichine Nikolai. Simulation of the formation and propagation of streamers in SF6and its mixtures[C]. XV International Conference on Gas Discharges and their Applications, Toulouse, 2004:315-318.
[12] Birdsall C K. Particle-in-cell charged-particle simulations,plus Monte Carlo collisions with neutral atoms,PIC-MCC[J]. IEEE Transactions on Plasma Science,1991, 19(2): 65-85.
[13] Pfeiffer W, Schoen D, Tong L. Simulation of predischarge processes in SF6/N2mixtures stressed by very fast transient voltages[C]. Conference on Electrical Insulation and Dielectric Phenomena, 1999: 391-394.
[14] 徐钟济. 蒙特卡罗方法[M]. 上海: 上海科学技术出版社, 1985.
[15] 裴鹿成. 蒙特卡罗方法及其在粒子输运中问题中应用[M]. 北京: 科学出版社. 1980.

