基于双d-q坐标系的并网逆变器控制策略

吴云亚 阚加荣 谢少军

（1. 盐城工学院实验教学部 盐城 224051 2. 南京航空航天大学自动化学院 南京 210016）

1 引言

太阳能、风能以及燃料电池作为新型清洁的能源受到了广泛的关注，利用这些能源的分布式发电技术成为全球能源可持续发展战略的重要组成部分[1]。新能源分布式发电的一个研究热点是逆变器并网控制技术[2]和PWM整流技术[3]。由于并网逆变器和 PWM整流器常采用相同的主电路结构，具有相同的数学模型，所以其控制原理也类似，而且同一 PWM变换器可以处于并网状态，也可以处于单位功率因数整流状态[4]。

PWM 变流技术主要包括直接电流控制技术[5]和间接电流控制技术[6]。直接电流控制对输入电流进行闭环控制，通过电流调节器的作用使交流电流实际值紧跟给定值，动态性能好，但存在孤岛状态时控制模式转换的问题[7]。而间接电流控制技术调节逆变器基准电压的幅值和相位来调节电流的大小和相位，尽管其动态响应较慢，而且还存在瞬态直流电流偏移问题，但其稳态性能好，控制结构简单，开关特性良好，易于微机实现，并且解决了模式转换时的无缝切换问题，如果在间接电流控制策略中加入补偿环节，也可以大大提高其动态特性。因此间接电流控制策略仍有非常大的应用空间。

传统的间接电流控制方法中[8]，逆变器的基准电压的相位角和幅值通过公式计算而来，所用的量包括电感值，而电感值在工作过程中可能受多种因素影响而发生变化，会造成幅值和相位角计算不准确；文献[9]提出了一种改进的间接电流控制方法，将逆变器的基准电压幅值始终等于电网电压的幅值，将进网电流闭环以调节逆变器基准电压的相位，从而实现逆变器并网，该方法不需要直接计算逆变器基准电压的相位角和幅值，克服了传统间接电流控制方法的缺点，但它未对逆变器基准电压的幅值进行调节，进网电流与电网电压必然存在相位差，造成进网功率因数小于1。

本文根据并网逆变器的数学模型，将间接电流的控制机理用于解释直接电流控制，在同步旋转d-q坐标下提出了一种简单的新型并网逆变器间接电流控制策略，该控制策略的系统功率因数受线路等效电阻和电网电压检测精度的影响，为解决此问题，在该控制策略的基础上，首次提出了一种基于同步旋转的双d-q坐标的间接电流控制策略，该方法消除了线路等效阻抗对功率因数控制的影响，使系统稳定在单位功率因数运行。

2 并网逆变器的数学模型及传统控制策略

三相电压型并网逆变器的拓扑结构如图 1所示，其中ea、eb、ec分别为三相电网电压，ua、ub、uc分别为三相逆变器三个桥臂中点电压，ia、ib、ic为三相进网电流，L、R为电感和线路等效电阻。则三相并网逆变器在d-q坐标系下的数学模型为[10]

式中，ud、uq为 d-q坐标系下三相并网逆变器输出电压；ed、eq为电网电压的 d、q轴分量；id、iq为进网电流的d、q分量；ωs为电网电压角频率。

图1 三相并网逆变器主电路Fig.1 Main circuit of three-phase grid-connected inverter

2.1 直接电流控制策略

如果将电网电压合成矢量E的幅值与d-q坐标中的d轴重合，则

那么逆变器输入到电网的有功功率和无功功率为

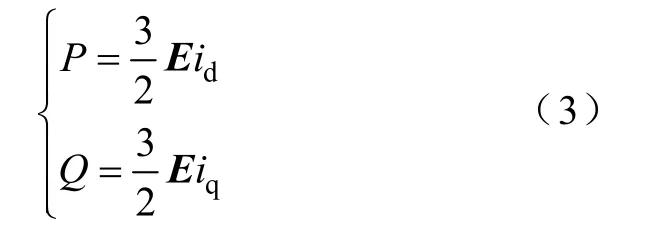
由式（3）可知，三相并网系统输出的有功可由d轴电流进行调节，无功可由 q轴电流调节。因此在同步旋转坐标系下通过对d-q轴电流分别控制就可实现并网系统输送到电网的有功和无功的解耦控制。传统的三相逆变器并网控制策略如图 2所示。

图2 传统并网逆变器控制策略Fig.2 Conventional control strategy for three-phase grid-connected inverter

由电网电压经 Clark变换得到电网等效合成矢量的旋转角θ，再由进网电流与该旋转角得到id和iq，将这两个量分别作为 d轴电流闭环和 q轴电流闭环的反馈量，分别经各自的PI调节器得到逆变器输出电压d轴和q轴的电压基准，再经空间矢量调制法得到六个开关管的驱动信号。

虽然传统的并网控制策略可以取得较好的并网效果，但是经双PI调节器得到的逆变器输出电压在d轴和q轴中基准值的形成机理不是很明确，两个电压基准在调节过程中的相互影响而使电流的跟踪速度较慢[11]。

2.2 间接电流控制策略

图3给出了并网逆变器a相等效电路以及在单位功率因数时的矢量图，可以看出调节逆变器输出电压的相位φ与幅值（调制比m）可以保证并网逆变器恒定向电网提供电流。其φ与m的表达式为

根据式（4）求得的相位和调制比控制并网逆变器运行，保证逆变器功率因数为1。

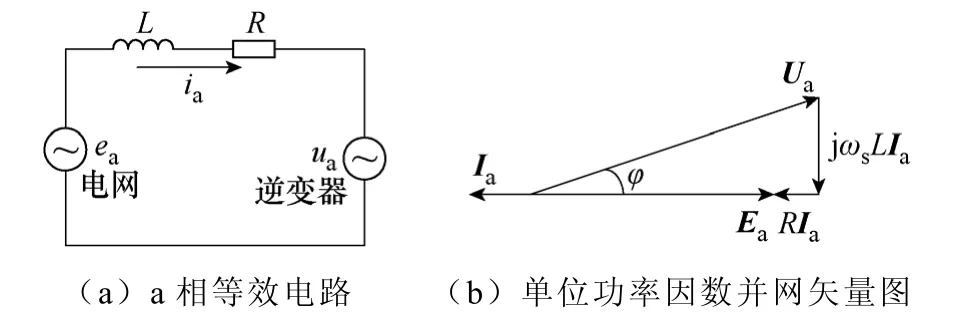
图3 间接电流控制策略Fig.3 Indirect current control strategy

间接电流控制方法需要电路中的一些易变量（如L和R）参与运算，其控制精度不高，此外，逆变器的相位调节精度受数字控制芯片调节精度的影响，从而影响到并网的控制效果。

3 新颖的并网控制策略

3.1 新颖并网控制策略的提出

图 3b是在静止坐标系下一相的电压和电流矢量图，而逆变器三相电压和电流与d-q旋转坐标相对静止，那么可以将三相并网逆变器的电压量和电流量的矢量图以直流不变量的形式体现在 d-q旋转坐标中。图4给出了在忽略线路等效电阻情况下，三相逆变器电压和电流的矢量图。

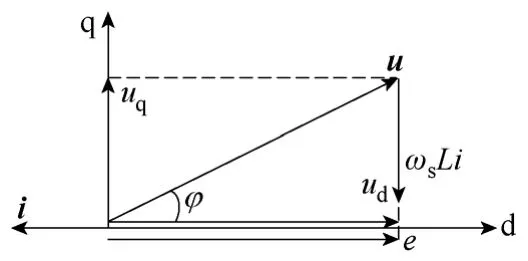
图4 忽略线路阻抗时逆变器矢量图Fig.4 Vector diagram ignoring R

由图4可以看出，在忽略线路电阻的情况下，逆变器单位功率因数运行时总有

而调节逆变器电压的q轴分量uq既可以调节逆变器的合成电压矢量u的幅值，又可以调节逆变器输出电压与电网电压之间的相位差φ。而并网电流i（单位功率因数时=id）的幅值与uq的关系为

所以，只要控制id就可以调节uq的大小，从而控制逆变器的幅值和相位，使逆变器稳定运行。图 5给出了新型并网策略的控制框图。图中将检测到的电网电压合成矢量的幅值作为逆变器输出电压d轴分量ud的基准，只使用了 1个 PI调节器就可以调节逆变器输出电压的幅值和相位，简化了调节系统。

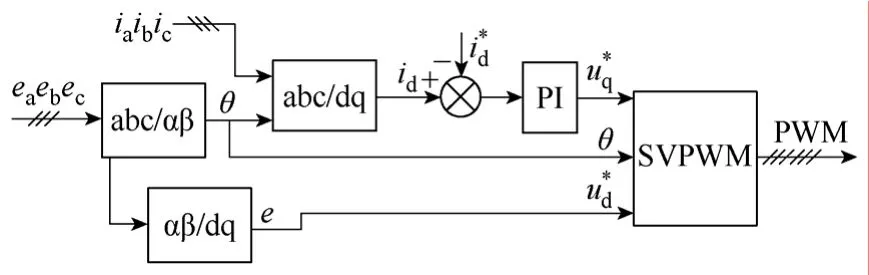
图5 新颖的并网控制策略Fig.5 Novel grid-connected control strategy

3.2 新型并网控制策略下参数对功率因数的影响

（1）线路等效阻抗对功率因数的影响。图 5

所示的框图是在在忽略线路电阻情况下得到的控制策略，但线路电阻不可避免，图6给出了在考虑线路等效阻抗时三相逆变器矢量图。可以看出，在R≠0

时，并网功率因数不为1，其值为

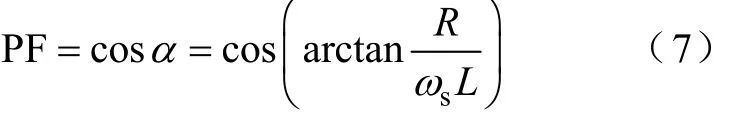
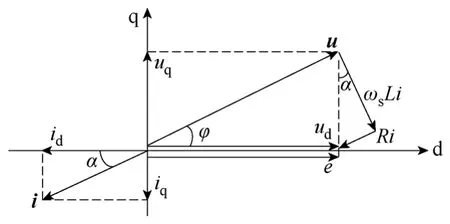
图6 考虑线路阻抗时逆变器矢量图Fig.6 Vector diagram considering R

在并网电感值较大时，逆变器的并网功率因数较接近于 1，但是过大的电感值会影响系统的动态调节性能。

（2）电网电压检测精度对功率因数的影响。三相电网电压是通过电压传感器，再经调制电路与A-D转换电路变为数字信号，这其中的任何一个环节都可能出现误差，都会使逆变器的d轴电压基准与电网的实际电压值有一定的偏离，图7分别给出了检测电压偏大和偏小两种情况下的电压电流矢量图。

图7 考虑电网电压偏差时逆变器矢量图Fig.7 Vector diagram considering difference between detecting and actual voltage

在图5所示的并网策略控制下，闭环量是电网电流的d轴分量，因此在系统稳定的范围内，系统输出的id大小相等。根据图7所示的几何关系，可以求得当电网电压检测值与实际值存在偏差时逆变器的并网功率因数

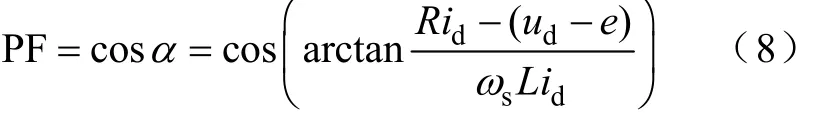
定义电压误差比

根据式（8）得到了逆变器并网功率因数受参数变化影响的曲线，如图8所示。图8a为电感值、d轴电流固定，功率因数受线路阻抗变化的影响，可以看出，在电压误差比为负值时，线路阻抗越大，功率因数越低；当电压误差比由负变为正的过程中，功率因数逐渐趋近于 1，但线路阻抗较大时需要较大的电压正偏置才能达到单位功率因数；随着电压误差比的进一步增大，功率因数又下降到1以下。图8b为电感值与线路等效阻抗不变时，逆变器的基准电流发生变化时的曲线，可以看出，电流越小，功率因数受电压误差比变化的影响越大，这对并网系统控制是非常不利的。

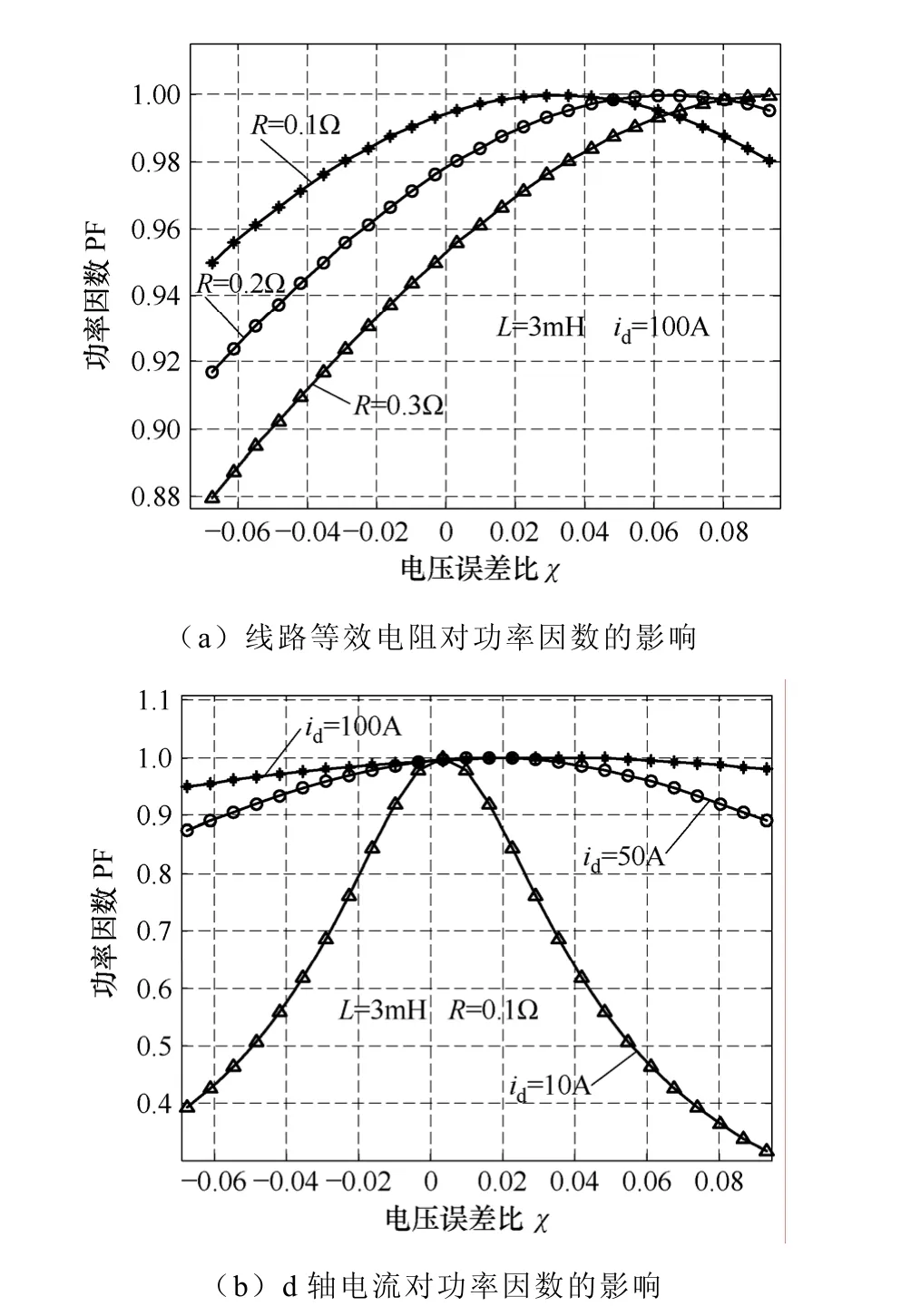
图8 参数变化对功率因数的影响Fig.8 Power factor affected by varying parameters

可以看出，本文所提的新颖的并网控制策略在线路电阻值小、处理功率大的时候可以获得较高的功率因数，如果达到IEEE Std 929—2000[12]的功率因数标准时，这是一种非常简单实用的并网方法。但是在功率因数低于文献[12]的规定时，需要找出提高并网功率因数的新方法。

4 基于双d-q坐标系下的并网控制策略

采用图5所示控制策略并网逆变器的功率因数受参数变化影响，最根本原因是并网电流的q轴分量不受闭环控制，为此必须引入iq闭环以控制使并网逆变器的功率因数为 1。在电网峰值电压与 d轴基准电压ud都不变时，与图7所示的矢量图相比，逆变器的输出电流i幅值变小，因此线路等效电阻以及并网电感上的压降的幅值减小，那么逆变器输出电压的合成矢量u的幅值将发生变化，在一个坐标系内，u变化，而ud不变是不成立的，因此需要将其中的一个量建立在另一个同步旋转、相差一定角度的坐标系d1-q1里。利用iq闭环的输出调制量控制两个同步旋转坐标的相位差，其矢量图如图 9所示。

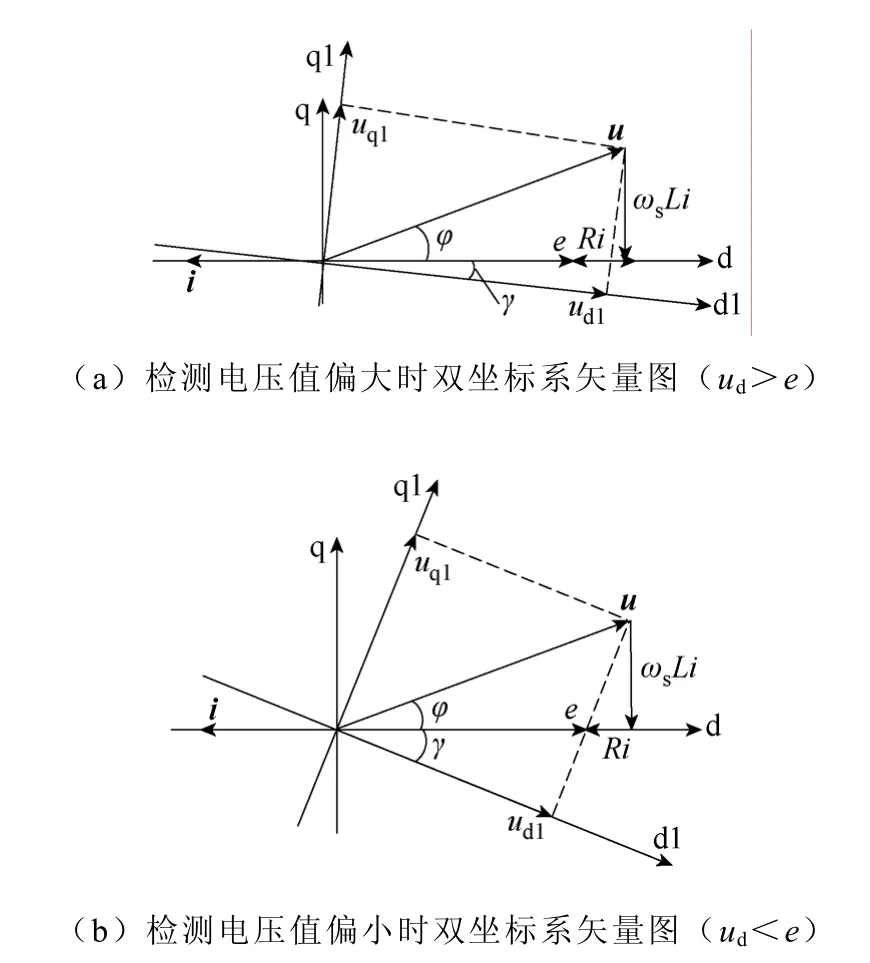
图9 双d-q坐标矢量图Fig.9 Vector diagram in double d-q coordinate

图9中，如果d-q轴与静止abc坐标或者静止αβ坐标的相对位置相差θ，那么d1-q1坐标就与静止坐标的相对位置差θ-γ，将逆变器输出电压的基准值落在坐标d1-q1中，并在该坐标中合成输出电压u。虽然矢量图中有两个坐标，但矢量图中的任何量的加减运算都满足平行四边形法则，所以在引入iq闭环以后，在d-q坐标中u，ωsLi，Ri以及e正好构成一个闭合的三角形，即并网电流正好与电网电压反向，实现单位功率因数并网。

由图9中的几何关系，可以得出逆变器输出电压合成矢量与d轴夹角为

而d1-q1坐标需要在d-q坐标的基础上再旋转

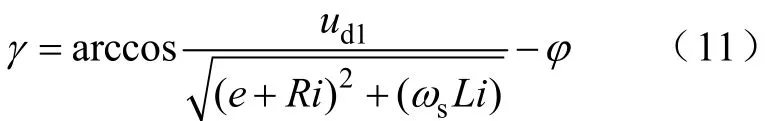
图 10为两个同步旋转坐标的相位差随电网电压检测值不同的变化曲线。可以看出，不管电网电压的检测值与实际值相比是偏大、偏小或者是正好相等，总能找到两个坐标之间合适的相位差以满足逆变器的并网功率因数等于1。

具体的控制框图如图11所示。

5 仿真验证

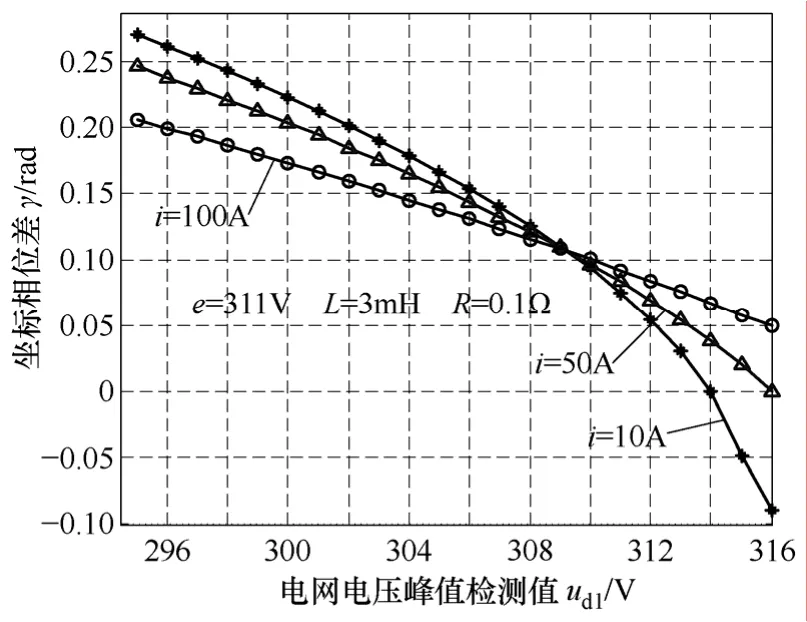
图10 双d-q坐标相位差Fig.10 Phase difference between double d-q coordinates

图11 双d-q坐标并网控制策略Fig.11 Grid-connected control strategy in double d-q coordinates

表 系统仿真参数Tab. Simulation parameters

根据本文所提的控制方案，用Matlab 7.1仿真软件建立了三相并网逆变器的仿真模型，对照图 1的主电路和图11所示的控制框图，给出了一组仿真数据，如下表所示。图12为电网相电压为e=311V，而检测给定逆变器d轴基准电压=300V，未采用双d-q坐标控制策略时的仿真波形。图12a为逆变器q轴电压基准、逆变器输出电流的d轴分量id和q轴分量iq的仿真波形，可以看出，逆变器虽然可以稳定工作，但是因为线路阻抗R与电网电压检测误差γ的影响使得iq≠0，从而逆变器的输出功率因数小于 1。图12b为逆变器输出电流波形，可以看出，逆变器的输出电流的幅值大于基准给定100A，这是由电流q轴分量iq≠0造成的。

图12 单d轴电流闭环控制仿真波形Fig.12 Simulation result with a single iq closed-loop

图13为电网相电压幅值为311V，而检测给定逆变器d轴基准电压=300V，采用双d-q坐标控制策略时的仿真波形，在0.35s处电流基准由100A向50A发生突变。图13a为在双d-q坐标控制策略下，由于d轴电流和q轴电流都采用了闭环控制，使得id和iq都跟踪给定基准值，因此三相并网逆变器可以实现单位功率因数运行，并且从图13b看出，逆变器输出电流的幅值正好等于d轴电流基准。图 13c为 q轴电流闭环调节器的输出，作为 d1-q1坐标轴与d-q坐标轴之间的相位差，其值与图10理论分析中的数据吻合。图13d给出了进网电流突变时电压、电流相位的变化过程，在电流突变时，电流的相位始终跟随电网电压的相位。可以看出引入d1-q1坐标轴后，系统的调节过程更加平缓，稳定性提高。

图13 双d-q轴电流闭环控制仿真波形Fig.13 Simulation result with double d-q control strategy

如检测电网电压偏大，会得到相同的并网控制效果。

6 结论

本文分析了三相并网逆变器系统，提出了一种新型的双d-q坐标系下的并网逆变器控制策略：

（1）在忽略线路电阻时，设定逆变器电压的d

轴基准值等于电网电压峰值，通过调节逆变器输出电流id就可以实现单位功率因数运行。

（2）线路阻抗会降低该并网控制策略的功率因数。

（3）电网电压检测的准确度也会降低该方法的并网功率因数。

（4）提出一种双 d-q坐标系下的并网控制策略，通过将逆变器d轴和q轴电压基准建立在新的d1-q1坐标系中，使逆变器输出电流的 q轴分量等于0，从而实现单位功率因数运行。

仿真结果表明，所提双d-q坐标系下的并网控制策略具有优良的性能。

[1] Nigim K A, Zobaa A F. Development and opportunities of distributed generation fuelled by renewable energy sources[J]. International Journal of Global Energy Issues, 2006, 26(3): 215-231.

[2] 姚志垒, 王赞, 肖岚, 等. 一种新的逆变器并网控制策略的研究[J]. 中国电机工程学报, 2006, 26(18):61-64.

Yao Zhilei, Wang Zan, Xiao Lan, et al. Research on a novel grid-connected control strategy of inverter[J].Proceedings of the CSEE, 2006, 26(18): 61-64.

[3] Lee T S. Lagrangian modeling and passivity-based control of three-phase AC-DC voltage-source converters[J]. IEEE Transactions on Industrial Electronics, 2004, 51(4): 892-902.

[4] 张纯江, 郭忠南, 王芹, 等. 基于新型相位幅值控制的三相 PWM整流器双向工作状态分析[J]. 中国电机工程学报, 2006, 26(11): 167-171.

Zhang Chunjiang, Guo Zhongnan, Wang Qin, et al.Analysis of bi-direction operation state of three phase rectifier based on a new phase and amplitude control[J]. Proceedings of the CSEE, 2006, 26(11):167-171.

[5] Ho M T, Chung H. An integrated inverter with maximum power tracking for grid-connected PV systems[J]. IEEE Transactions on Power Electronics,2005, 20(4): 953-962.

[6] Taesik Yu, Sewan Choi, Hyosung Kim. Indirect current control algorithm for utility interactive inverters for seamless transfer[C]. IEEE PESC, 2006,1-6.

[7] Tirumala R, Mohan N, Henze C. Seamless transfer of grid-connected PWM inverters between utility-interactive and stand-alone modes[C]. IEEE Applied Power Electronics Conference, Dallas, USA, 2002: 1081-1086

[8] Dixon J W, Ooi B T. Indirect current control of a unity power factor sinusoidal current boost type three-phase rectifier[J]. IEEE Transactions on Industrial Electronics, 1998, 35(3): 508-515.

[9] Hyosung Kim, Taesik Yu, Sewan Choi. Indirect current control algorithm for utility interactive inverters in distributed generation systems[J]. IEEE Transactions on Power Electronics, 2008, 23(3):1342-1347.

[10] Blasko V, Kaura V. A new mathematical model and control of a three-phase AC-DC voltage source converter[J]. IEEE Transactions on Power Electronics,1997, 12(1): 116-123.

[11] 钟炎平, 沈颂华. PWM整流器的一种快速电流控制方法[J]. 中国电机工程学报, 2005, 25(12): 52-56.

Zhong Yanping, Shen Songhua. A fast current control scheme for PWM rectifier[J]. Proceedings of the CSEE, 2005, 25(12): 52-56.

[12] IEEE-SA Standards Board. IEEE Std 929-2000 IEEE recommended practice for utility interface of photovoltaic(PV) systems[S]. New York: The Institute of Electrical and Electronics Engineers, Inc., 2000.