一种适用于航空电力作动器负载的三相PWM整流器最大功率控制

张 巍 尚晓磊 周元钧 刘欣博 韩红伟

(1. 北京航空航天大学自动化科学与电气工程学院 北京 100191 2. 中国特种设备检测研究院 北京 100013)

1 引言

三相电压源 PWM整流器具有高功率因数、几乎正弦的输入电流和双向能量流动能力等诱人特性[1]，因此越来越被视为替代传统二极管不控整流器和晶闸管相控整流器的一种理想AC-DC变换器，并在很多工业领域得到了广泛地研究和应用。然而，到目前为止，PWM 整流器在航空领域的应用还极为少见。随着多电飞机日益成为未来飞机的发展方向，机载电驱动装置急剧增加，为保证飞机电网的品质和电能利用效率，有必要开展PWM整流器在该领域的研究。

航空电力作动器肩负着驱动飞机舵面的任务，是未来多电飞机电力系统的重要负载[2-3]。据估计，在未来飞机上，电力作动器负载将占到飞机电功率的 75%以上[4]。不同于普通机电设备，由于快速起动和制动要求，电力作动设备的用电功率具有大范围快速变化的特性；并且，由于闭环控制，使其在小信号分析中具有恒功率负载特性。因此，该负载对 PWM 整流器的输出稳定将是一个极大考验。

在此之前，已有很多有关 PWM整流器的研究成果得到发表。这些成果可以归纳为两类：线性控制和非线性控制。由于PWM整流器本身具有很强的非线性特性，线性控制难以达到理想控制性能，近年来非线性控制策略得到了广泛的研究，并取得了大量的成果，例如：反馈线性化[5]、基于利亚普诺夫函数的控制[6]、基于无源控制理论的控制策略[7-8]、直接功率控制[9]等都得到了很好的效果。然而，这些非线性控制器的设计或者比较复杂，工程应用有一定难度，或者是基于滞环比较产生 PWM信号，开关频率不可控，也会产生相应的问题。因此，在工程实际中应用最为广泛的还是传统的旋转坐标系下 PI调节器控制的双闭环控制策略[10-11]。而这是一种典型的线性控制策略，在负载大范围扰动下难以保证系统稳定。因此，需要一种既可抗大范围扰动，控制方法又简单易行的工程应用新方案。

本文针对航空电力作动器功率大范围变化的特性，在传统双闭环控制基础上，提出了一种最大功率输出控制策略。采用此方案，不仅可以在动态负载大扰动下获得小的动态压降，具有较好的稳定性，而且能够方便工程应用。

2 PWM整流器的模型分析及最大功率控制方法的提出

2.1 三相VSR的拓扑结构及数学模型

三相电压型 PWM整流器（VSR）的拓扑结构如图1所示，图中假定是一个电阻型的负载RL接在整流器的直流输出端[1]。在同步旋转坐标系（dq坐标系）下，其数学模型为[12]

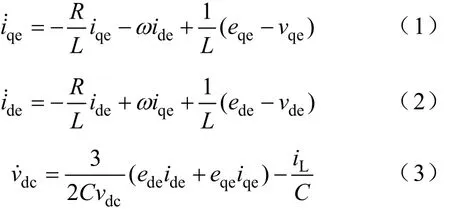
式中edqe，—dq坐标系下电源电压;

idqe，—dq坐标系下电源电流；

vdqe—整流器交流侧电压；

R，L—电阻和输入端电感；

ω—同步角频率；

vdc，idc—直流侧输出电压和电流；

iL—负载电流；

RL—负载电阻。

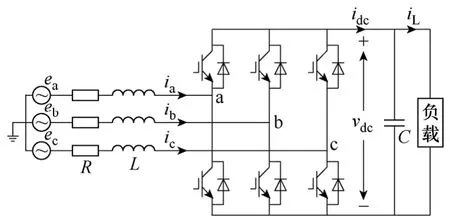
图1 三相电压型PWM整流器拓扑结构Fig.1 AC-DC voltage source PWM converter

2.2 三相VSR电流前馈解耦的双闭环控制策略

同步旋转坐标系下前馈电流解耦控制策略已成为 PWM整流器工程应用中的标准解决方案，其电流环、电压环控制结构分别如图2和图3所示。

2.2.1电流内环调节器

电流内环调节器如图2所示[12-13]。在同步旋转坐标系下，将电流分为无功电流ide和有功电流iqe，采用PI调节器分别进行控制。在这种控制策略中，采用电流前馈的方式消除整流器数学模型中的耦合项ωLide和ωLiqe，使得有功电流iqe可以独立于ide和vdc进行控制，实现了解耦。同样地，ide的控制也独立于iqe和vdc。为得到单位功率因数控制，无功电流ide的给定值一般设为零，而iqe由电压外环调节器的输出给定。

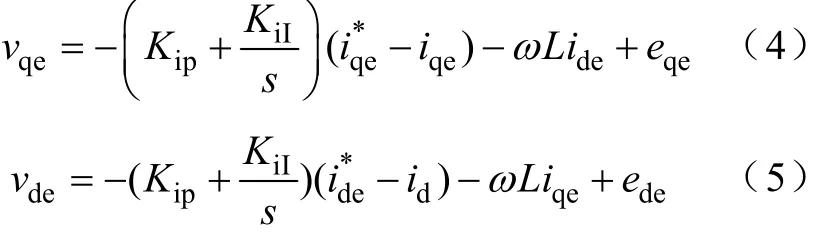
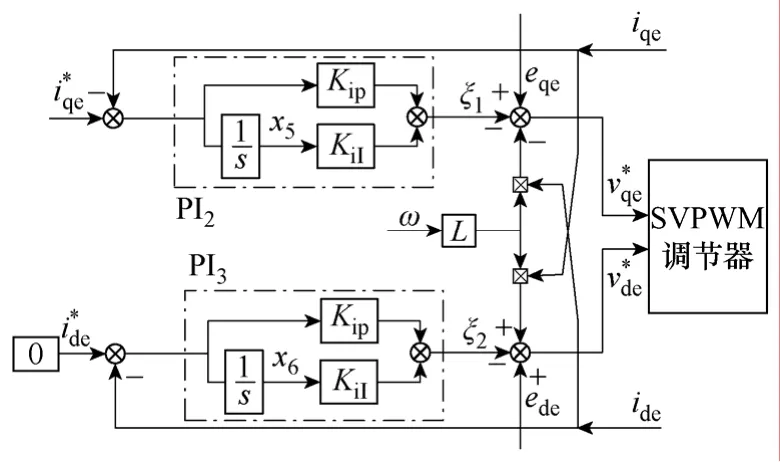
图2 电流调节器的结构框图Fig.2 Block diagram of the current controller

电流调节器的控制方程为2.2.2电压外环调节器

电压外环的结构框图如图3所示，以直流侧电压测量值作为负反馈与电压给定值相比较而得的误差值经过PI调节器调节后，得到电流内环iqe的给定值。

电压调节器的方程为

图3 电压调节器的结构框图Fig.3 Block diagram of the voltage controller

在设计时，电流内环PI调节器的快速性要求比电压外环 PI调节器高出很多（5倍以上）。如此一来，可认为电流具有即时跟踪能力，但在负载快速变化时，往往会因电压跟踪不能及时到位而出现大的动态压降或压升，甚至引起不稳定。

2.3 最大功率控制方案的提出

三相滤波电感L的设计是PWM整流器设计的关键，一般按照额定功率来设计电感值，且设计值与额定功率成反比关系。然而，电感不但会影响整流器的输出功率，还对输入端的谐波有很大影响。对于某些大范围变化的负载，例如航空电力作动器，若按照峰值功率设计整流器，则电感值偏小，导致输入侧谐波含量高，甚至电流不连续，违背了采用PWM 整流器改善电网谐波的初衷；而若按较低功率设计，在负载功率较大时，易引起整流器不稳定。下面将提出一种最大功率控制方法，扩大整流器输出功率范围。可按较小功率设计电感，通过最大功率控制，使之能够满足负载峰值功率的需求，保证整流器稳定工作并使输入电流具有更低的谐波含量。

在同步旋转坐标系（dq坐标系）中，采用“等功率”坐标变化，则三相电压型 PWM整流器的有功功率p和无功功率q的静态值、可表达为[14]

一般同步旋转坐标系的初始角设为与电源电压a相重合，因此有

式中，Em为dq坐标系下的供电电源电压。

而 d轴电流静态值和 q轴电流静态值表达式为[15]

式中，φ1表示电网电动势初始相角，φ2表示开关函数基波分量的初始相角，dm为开关函数稳态值。

将式（9）、式（10）、式（11）、式（12）代入式（7）和式（8）可得

分析式（13）和式（14），当可视为常值，有功功率和无功功率只与有关。在一般情况下，采用单位功率因数控制，即无功功率，于是有

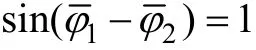
2.4 结合最大功率控制的PWM整流器双闭环控制策略

根据 2.3节的分析可知，最大功率控制方案必须有条件地应用，其作用应只在瞬时功率无法满足负载需求时发挥，这样才能保证正常工作时的高性能单位功率因数整流和负载大范围变化时的输出性能。根据这样的限定，确定使用最大功率变化控制的条件为：①电流达到某限定值；②动态压降达到某限定值。二者必须同时满足，缓慢变化的负载电流不至于引起大的动态压降，采用普通双闭环调节足以满足要求，因此最大功率控制不需介入。而如果只考虑压降而不考虑电流值则可能引起控制系统的不稳定，两者综合考虑才能达到好的性能。

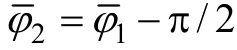
S为切换控制信号，且满足方程

式中

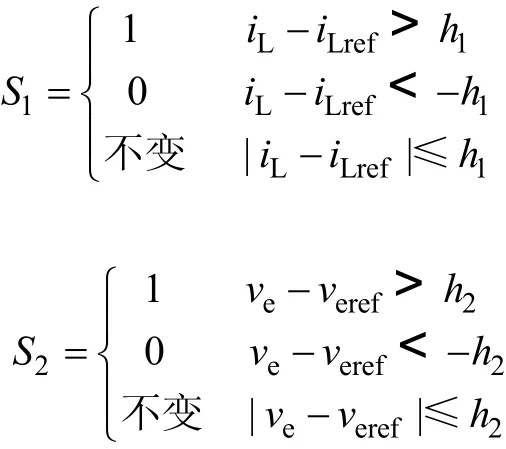
式中，iLref表示参考负载电流，veref为参考直流电压误差；h1为电流滞环死区，h2为电压误差滞环死区，均为正值。

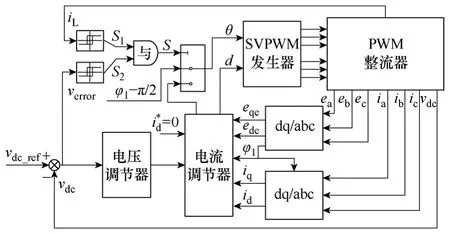
图4 最大功率控制与传统双闭环控制相结合的系统框图Fig.4 Structure of the proposed control method

3 航空电力作动器负载特性分析

3.1 电力作动器的动态特性

电力作动器驱动飞机舵面时，要求很高的快速性。将飞机舵面负载转矩折合到电动机轴上，得到电动机的转矩方程为

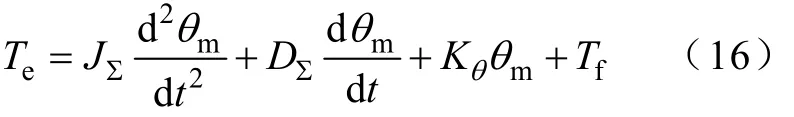
图5描述了某电力作动器负载驱动舵面移动较大偏角时功率变化过程。根据式（16）的数学模型，此动态过程可以分为三个阶段[16]：

（1）输入电能加速电动机和负载惯性。

（2）舵面驱动负载（电动机提供速度和转矩）。

（3）舵面维持负载（电动机提供转矩但无速度）。

在两种情况下出现峰值功率，首先是电动机起动时，由于飞机舵面的快速性要求需要很大的加速度，从而导致电流/功率大幅度冲击。其次是当舵面大角度运动时，由于铰链力矩随着舵面偏转角度增加而增加，当偏转到大角度时产生大功率/电流。

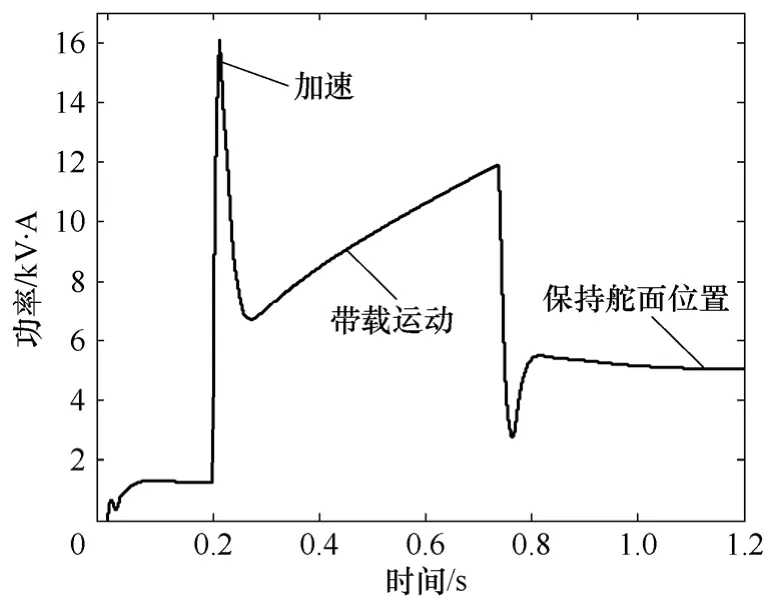
图5 某电力作动器运动时的功率剖面Fig.5 Dynamic load profile of an electric actuator

3.2 电力作动器的恒功率特性

恒功率负载（constant power load）是指具有功率恒定不变的一类负载特性，一个理想的恒功率负载可以抽象为一个标准的非线性模型，即iL=Po/v。从长时间来看电力作动器系统是一种功率大范围快速变化的负载，并不具备恒功率特性。但是进行小信号分析可知，由于闭环控制的作用使得航空电力作动器具有恒功率特性。其特性可以描述为iL=P(t)/v。这表明，若由于电流iL动态增大，而引起电源产生压降，那么iL将会变得更大，引起更大的压降，形成恶性循环。同样iL迅速减小时，电源产生升压也会有类似的效果。

综上所述，电力作动器对电源而言是一个具有恒功率特性、大范围快速变化的动态负载。负载功率达到峰值的时间非常短（10～20ms），绝大部分时间维持一个较小功率需求，按峰值功率设计其电源显然不合适。但电源必须具有在短时间内产生一个峰值功率输出的能力，将最大功率方法控制的PWM 整流器用于航空电力作动器负载显得极具意义。

4 仿真结果

4.1 整流器参数

基于图 1的拓扑结构建立的一个三相电压源PWM整流器的仿真模型的电气参数见下表[17-18]，该模型采用Matlab/Simulink建立。

4.2 负载参数

采用 Matlab/Simulink建立的航空电力作动器模型作为负载，其动态功率特性如图5所示，且负载特性采用理想恒功率负载的方式建模。要求在整个负载变化的动态过程中，PWM 整流器的动态压降应在10%以内。

表 PWM整流器仿真模型电气参数Tab. Specifications of the VSR

4.3 仿真结果

在本节中将普通双闭环控制系统与结合了最大功率控制的系统进行了对比仿真研究。

图6a～图6c是普通双闭环PI调节器在不同PI参数时的响应曲线。从图6a到图6c PI调节器快速性逐渐加大。从图6a中可见，由于PI调节器快速性较差，在0.2s时刻，负载电流突然增大，而输出电压不能快速跟踪，导致直接降到零输出，而由于理想恒功率特性，负载电流变为无穷大，这说明在这种情况下，系统是不稳定的。从图6b可见，虽然系统在负载的整个变化过程中保持稳定，但是在0.2s附近，由于负载动态变化非常大，导致输出电压产生较大的动态压降，输出最低降到了226.7V，不能满足压降在10%以内的要求，且电流峰值很大，对功率器件冲击较大。从图 6c可见，由于增大了PI调节的快速性，系统的动态压降满足了要求，但在0.5～0.75s时，系统出现了持续地振荡，这是不希望看到的。由此可见，普通双闭环结构对这种大范围变化负载的调节能力有限。

图 6d是采用本文提出的结合最大功率控制的双闭环控制结构的响应曲线。可见，在采用了这种结构后，输出的动态压降满足了要求，虽然在两种控制方法切换时产生了几次振荡，但这正是最大功率控制器控制效果的体现。当由于负载电流和动态压降条件满足，系统切换到最大功率控制方式，从而使得输出直流电压迅速上升，随着电压的上升，切换条件不再满足，系统控制由转换为普通线性PI控制，输出电压又再次降低，如此反复，产生了图中的振荡，这种振荡发生在电流峰值部分，其实其效果是使得输出电压保持在一个可以接受的范围之内，有利于系统的正常工作，且这个时间很短，是可以接受的。同时，可以看到图 6d中没有出现图6c中那样大范围长时间的振荡，因此控制效果优于图6c。在整个动态过程中，大部分时间系统采用普通双闭环控制方式工作，因此可以保证功率因数接近于单位功率因数，如图7a所示；电流迅速变化时采用最大功率控制策略，功率因数不再保持为单位功率因数，如图7b所示，但由于时间很短，不会对电网产生大的影响。

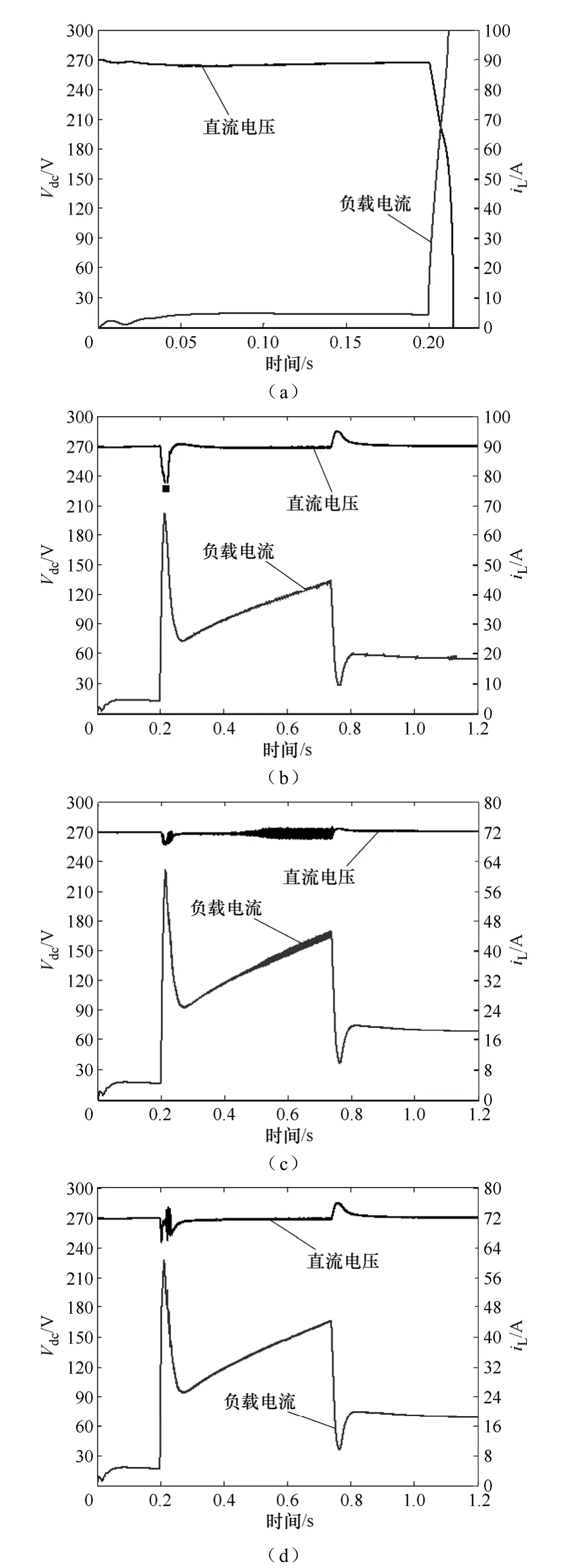
图6 不同控制器作用下输出端动态仿真结果Fig.6 Dynamic simulation results of the output terminal under different controllers

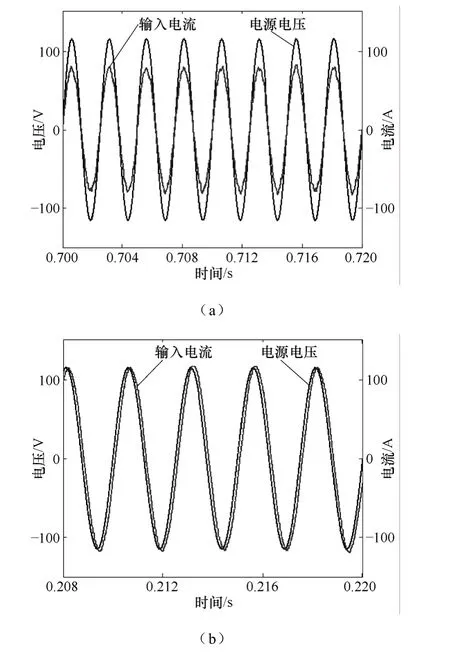
图7 电源侧电压和电流仿真波形Fig.7 Simulation waveforms of the source voltage and the input current

5 实验结果

以 TMS320F2812数字信号处理器为核心控制器，功率电路由智能功率模块（IPM）PM150CSA060、电抗器、电解电容器、功率电阻等组成了三相电压型 PWM整流器硬件电路。供电电源为三相400Hz交流电源，参数与表1中的仿真参数一致。以文献[19-20]中设计的10kW电力作动器样机作为负载。该航空电力作动器及其实验台如图 8所示。

图8 电力作动器及实验台Fig.8 Electric actuator and laboratory platform

图9 直流输出电压和负载电流实验波形Fig.9 Experimental results of the load current and output DC voltage

在上述实验设备上，分别采用最大功率控制器和普通PI控制器进行对比研究，得到直流端电压和负载电流的实验波形，如图9所示。示波器通道CH1为PWM整流器输出直流电压波形，采用霍尔电压传感器 CHV-20L检测，外接 2.7kΩ 输入电阻，输入输出比为 54:1，即在图 9中代表输出电压 54V/格。通道CH2为负载电流波形，采用霍尔电流传感器 LA-50T检测，采样电阻 100Ω，图中每格代表10A。图9a为采用最大功率控制方法所得波形，从电流曲线可以看到，实验中负载电流峰值达到约50A，折合最大功率约13.5kW。分析图9的电压波形可知，实验结果基本与仿真结果具有类似效果，在0.1～0.15s由于系统加速产生大峰值电流导致出现较大压降时，最大功率控制器发生作用，使电压振荡中保持稳定，没有形成过大压降。图9b是采用普通PI调节器所得实验波形，对比图9a可见，在负载电流迅速上升时，整流器直流侧出现较大压降，从而导致负载电流进一步上升。其峰值负载电流达到了56A，远高于图9a的46A，这正是由于线性控制器不能在负载动态变化时保持输出直流电压稳定而形成的。因此实验证明了本文提出的最大功率控制方法的有效性。

6 结论

到目前为止，在航空领域广泛使用着12脉冲、18脉冲、甚至24脉冲整流技术[17]，这种整流技术对于大功率负载而言，输入电流谐波等用电性能对于航空电网仍然不够理想，而且存在能量无法回馈的缺陷。而先进的 PWM整流技术在航空领域取代二极管整流已经是一种趋势。本文旨在将PWM整流技术引入航空领域中，针对该领域的一种特殊负载—电力作动器的需求进行了研究，提出了一种适合该类负载的整流控制方案，通过理论分析、仿真和实验结果表明，这种控制方案设计简单，效果明显，具有较强的实用性。

[1] Green A W, Boys J T, Gates G F. Three-phase voltage sourced reversible rectifier[J]. IEE Proceedings of Electric Power Applications, 1988, 135(6): 362-370.

[2] Rosero J A, Ortega J A, Aldabas E, et al. Moving towards a more electric aircraft[J]. IEEE Aerospace and Electronic Systems Magazine, 2007, 22(3): 3-9.

[3] Garcia A, Cusido J, Rosero J A, et al. Reliable electro-mechanical actuators in aircraft[J]. IEEE Aerospace and Electronic Systems Magazine, 2008,23(8): 19-25.

[4] Emadi K, Ehsani M. Aircraft power systems:technology, state of art, and future trends[J]. IEEE AES Systems Magazine, 2000, 15(1): 28-32.

[5] Lee D C, Lee G M, Lee K D. DC-bus voltage control of three-phase AC/DC PWM converters using feedback linearization[J]. IEEE Transactions on Industrial Application, 2000, 36(3): 826-833.

[6] Komurcugil H, Kukrer O. Lyapunov-based control for three phase PWM AC/DC voltage-source converters[J].IEEE Transactions on Power Electronics, 1998, 13(5):801-813.

[7] 张晓华, 张卫杰. 三相电压型 PWM 整流器的IDA-PB 控制[J]. 电工技术学报, 2009, 24(3):122-127.

Zhang Xiaohua, Zhang Weijie. IDA-PB control for three-phase PWM voltage source rectifier[J].Transactions of China Electrotechnical Society, 2009,24(3): 122-127.

[8] 王久和, 黄立培, 杨秀媛. 三相电压型PWM整流器的无源性功率控制[J]. 中国电机工程学报, 2008,28(21): 20-25.

Wang Jiuhe, Huang Lipei, Yang Xiuyuan. Power control of three-phase boost-type PWM rectifier based on passivity[J]. Proceedings of the CSEE, 2008,28(21): 20-25.

[9] 王久和, 李华德, 王立明. 电压型PWM整流器直接功率控制系统[J]. 中国电机工程学报, 2006, 26(18):54-60.

Wang Jiuhe, Li Huade, Wang Liming. Direct power control system of three phase boost type PWM rectifiers[J]. Proceedings of the CSEE, 2006, 26(18):54-60.

[10] Blasko V, Kaura V. A new mathematical model and control of a three-phase AC-DC voltage source converter[J]. IEEE Transactions on Power Electronics,1997, 12(1): 116-123.

[11] 瞿博, 吕征宇. 三相电压型 PWM 整流器小信号建模及其控制器设计[J]. 电工技术学报, 2010, 25(5):103-108.

Qu Bo, Lu Zhengyu. Small-signal modeling and controller design of three-phase voltage source PWM rectifier[J]. Transactions of China Electrotechnical Society, 2010, 25(5): 103-108.

[12] Lee D C. Advanced nonlinear control of three-phase PWM rectifiers[J]. IEE Proceedings of Electric Power Applications, 2000, 147(5): 361-366.

[13] Cichowlas M, Kazmierkowski, M P. Comparison of current control techniques for PWM rectifiers[C].International Symposium on Industrial Electronics,2002, 4: 1259-1263.

[14] 王兆安, 杨君, 刘进军. 谐波抑制和无功功率补偿[M]. 北京: 机械工业出版社, 1998.

[15] 张崇巍, 张兴. PWM整流器及其控制[M]. 北京: 机械工业出版社, 2003.

[16] Trainer D R, Whitley C R. Electric actuation—power quality management of aerospace flight control systems[C]. International Conference on Power Electronics, Machines and Drives, 2002: 229-234.

[17] Weimer J A. Electrical Power Technology for the More Electric Aircraft[C]. Digital Avionics Systems Conference, 1993: 445-450.

[18] Maldonado M A, Shah N M, Cleek K J, et al. Power management and distribution system for a more electric aircraft (MADMEL)-program status[C].Proceedings of the Intersociety Energy Conversion Engineering Conference, 1997, 1: 274-279.

[19] 董慧芬, 周元钧, 沈颂华. 双通道无刷直流电动机容错动态性能分析[J]. 中国电机工程学报, 2007,27(21): 89-94.

Dong Huifen, Zhou Yuanjun, Shen Songhua. Analysis on the fault-tolerant dynamic performance of a brush-less DC motor with double channels[J].Proceedings of the CSEE, 2007, 27(21): 89-94.

[20] 周元钧, 赵运坤, 葛云海. 复合式余度机电作动系统容错控制与性能分析[J]. 北京航空航天大学学报,2008, 34(3): 285-289.

Zhou Yuanjun, Zhao Yunkun, Ge Yunhai. Faulttolerant control method and characteristic analysis of hydraulic redundant EMA system[J]. Journal of Beijing University of Aeronautics and Astronautics,2008, 34(3): 285-289.