基于Matlab的三相APFC建模与仿真

彭卫东，刘小刚，张德银

(中国民用航空飞行学院，四川 广汉 618307)

1 引言

随着电力电子技术的发展，AC/DC、DC/DC、DC/AC等静止电力变换装置已广泛应用于电力、交通、冶金、化工、通讯、航空、航天等领域。电力电子装置多数通过整流器与电力网接口，传统的整流逆变电路采用的是二极管整流或者晶闸管相控整流，其网侧的功率因数低，而且电网谐波含量大，提高功率因数、消除和抑制谐波已成为电力电子领域研究的重大课题［1，2］。单相功率因数校正技术现在发展的比较成熟，在小功率场合有了广泛的应用。随着电力电子技术的发展，电力电子装置的功率越来越大，使得三相功率因数校正技术的研究有了较快速的发展。

三相六开关升压型PFC被认为是最有发展前途的数字控制三相PFC电路拓扑，其主要作用是将交流电变换成直流电，可作为电源开关的前级。它具有输入电流的谐波畸变小、功率因数近似等于1、直流侧电压稳定、动态响应快、效率高及能量可双向流动等优点，成为现在三相PFC研究热点。

2 三相PFC的工作原理

三相六开关升压型PFC实为PWM整流器，主电路图如图1所示，其工作原理是利用输出侧电容电压对输入侧进行反向调制，通过输入侧电感滤波使输入电流和输入电压同相且呈正弦波［3-5］。控制系统的设计包括电压外环和电流内环的双环设计。电压调节器作为外环调节，能稳定输出直流电压，使得输出直流电压比输入电压峰值高，且从频域角度分析，应限制电压调节环的带宽。电流环能使三相输入电流时刻跟随输入电压，在谐波量很低的情况下与电网电压同相，从而实现功率因数校正的目的。

此电路主要包括交流侧电感、直流输出电容以及由全控开关器件(IGBT)和续流二极管组成的三相桥式电路，ea、eb、ec为电源电压，ia、ib、ic为输入电流，RS为回路电阻，LS为三相滤波电感，RL为负载电阻。

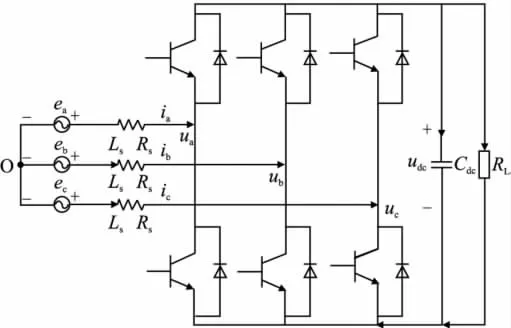
图1 三相六开关升压型PFC主电路

假设开关皆为理想开关，交流电源为三相对称理想电压源，三相回路等效电阻和电感相等，网侧滤波电感L是线性的，且不考虑饱和，忽略开关的死区时间，可得三相电网电压的时域表达式［6，7］:

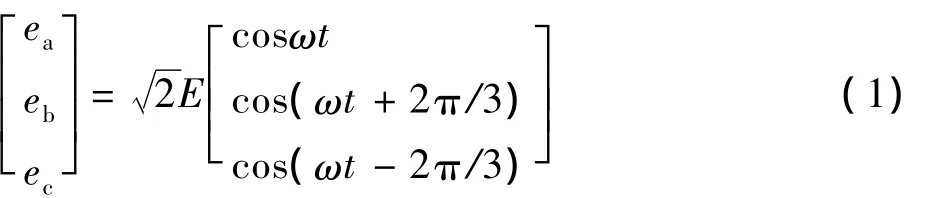
由基尔霍夫电压、电流定律可得:

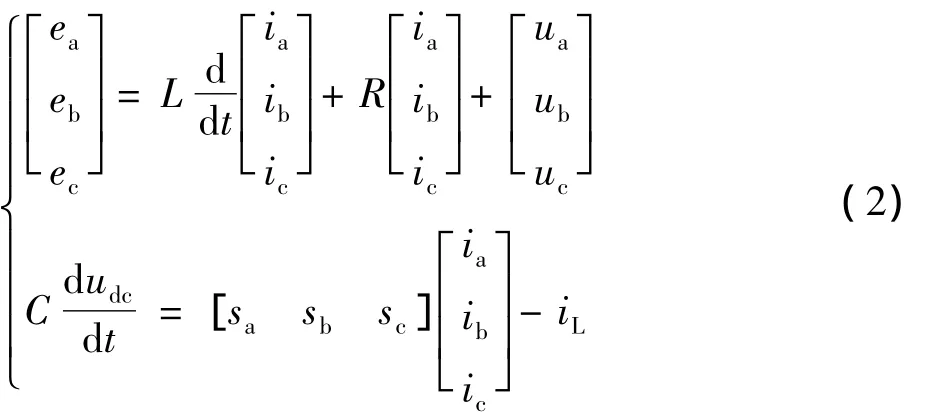
3 基于dq旋转坐标系的模型与解耦分析

在三相静止坐标系下，由于ea、eb、ec之间以及ia、ib、ic是时变交流量，且相互之间存在耦合，系统控制做不到无静差，不利于控制系统的设计。因此，通过派克变换转变为两相旋转坐标系下的数学模型。经过坐标变换后，三相对称静止坐标系中的基波正弦变量将转化为同步旋转坐标系中的直流变量，从而简化了控制系统的设计［6］。同步旋转坐标矢量关系如图2所示。

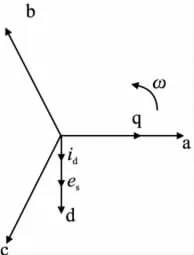
图2 同步旋转dq矢量坐标

坐标变换通常有“等量”变换和“等功率”变换两种方式，所谓“等量”变换是指坐标变换前后电气量的通用矢量相等，而“等功率”变换则是变换前后功率保持不变［7］。由于“等功率”变换保证了功率不变，但不易于理解，而且也容易对变换矩阵进行求逆运算，故本文采用“等功率”dq变换法来建立三相PFC的数学模型。

应用abc静止坐标到 dq旋转坐标同步变换Tabc/dq0有［8］:

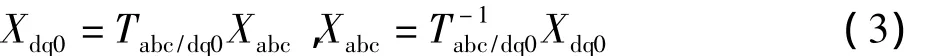
坐标变换矩阵为:

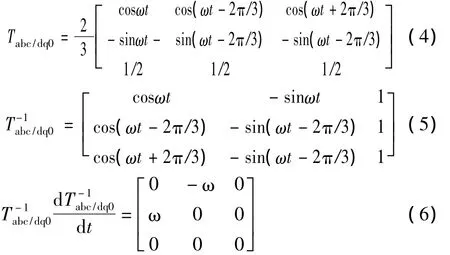
联立以上各式，可得

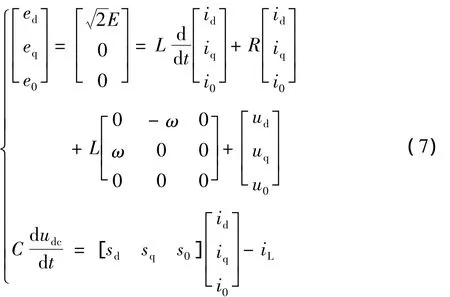
对于电网平衡下的三相PFC而言，有e0=0，i0=0。因此在dq旋转坐标系下三相PFC模型中0轴的方程可略去，最终得到dq旋转坐标系下三相PFC数学模型如下:

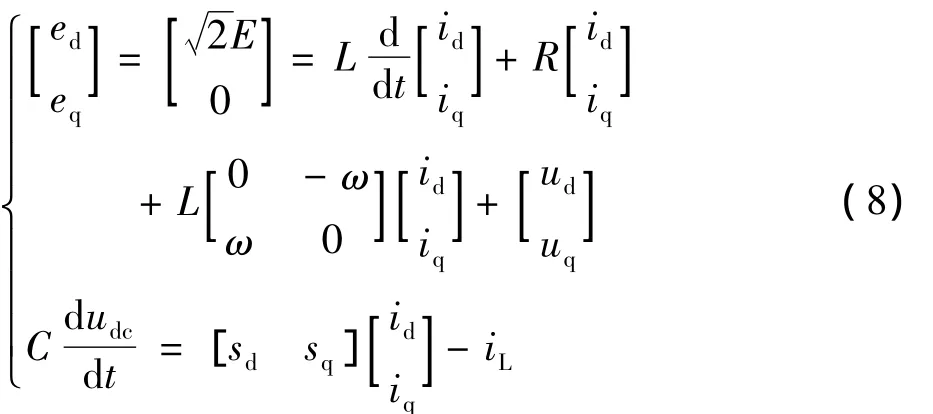
网侧输入有功功率和无功功率为:

网侧输入功率因数为:

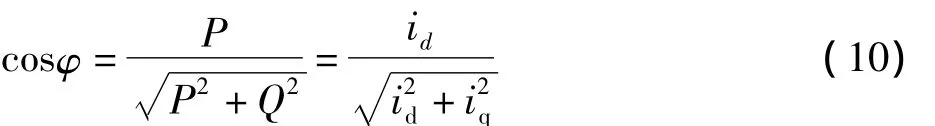
以上分析，把三相坐标系中的交流量变成了两相同步旋转坐标系中的直流量，实现了PFC输入的有功和无功的解耦，d轴电流id相当于有功功率的电流，q轴电流iq相当于无功功率的电流，为实现高性能的控制提供了条件。

4 控制与仿真研究

由前面的分析，采用前馈解耦方式设计控制器，可得到系统控制框图，如图3所示。

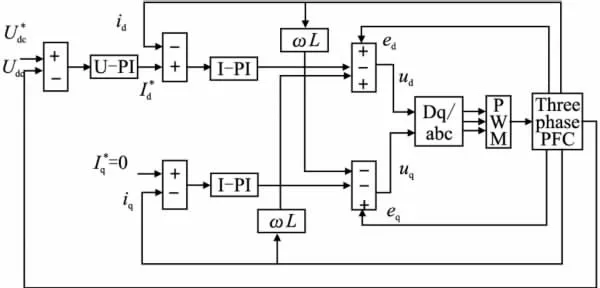
图3 系统控制框图

由图可以看出整个系统采用PI调节器［6］作为前馈控制器，是一个典型的双闭环调节系统，外环是电压环，内环是电流环，迫使输入电流跟随输入电压，提高系统动态性能。

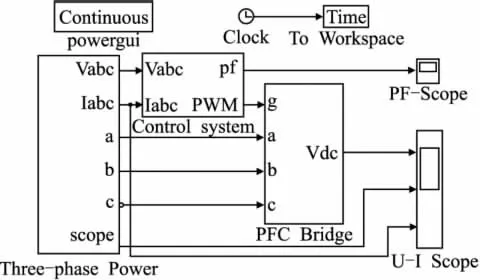
图4 Simulink仿真模型

根据图3的建立的系统控制器模型，系统仿真利用MATLAB R2009a中的Simulink仿真平台，搭建仿真模型如图4所示，进行仿真实验，设置仿真参数如表1。

表1 仿真参数

此仿真中，系统在a相正弦输入电压初始相位角为90°时开始运行，带9Ω负载起动直至稳定，系统直流侧输出电压在负载为16Ω时从400V下降到300V，以及系统负载从15Ω突变到10Ω进行了仿真，得到如下波形:

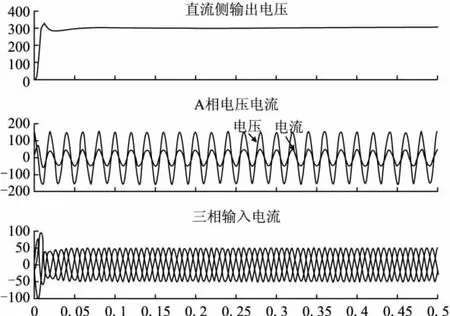
图5 负载9Ω时的波形

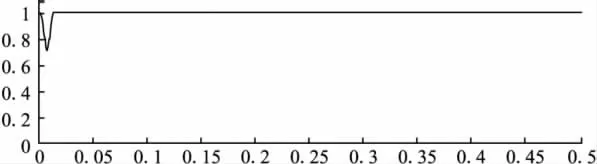
图6 系统的功率因数

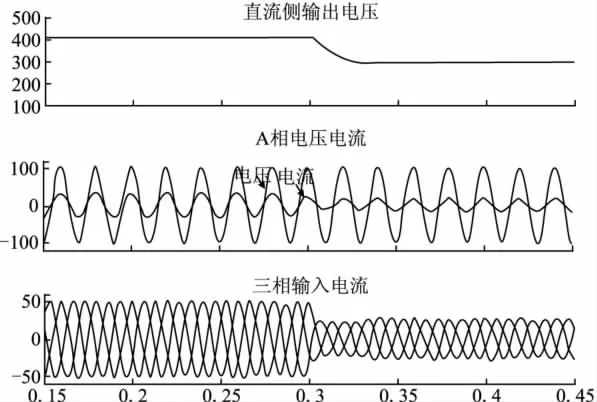
图7 直流侧电压突变时波形

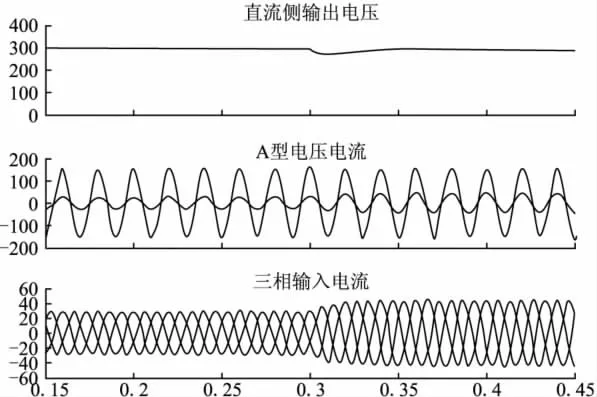
图8 负载突变时的波形

5 结论

综合以上仿真结果分析，网侧输入电流在宽输出范围内能很好地跟随网侧输入电压，实现了单位功率因数的整流效果;带载起动速度快，调整时间在0.05s以内，稳态精度高，网侧输入功率因数在0.98以上。负载突变和直流侧电压突变，响应速度快。输出功率10kW，达到大功率三相APFC的设计和仿真要求。

三相PFC整流器是一个时变非线性耦合系统，其控制是比较复杂的，硬件的工艺水平也是一个重要的影响因素。随着理论和技术的不断发展，三相PFC整流器的输出功率和控制性能将不断提高，应用也将越来越广泛，最终实现三相PFC的大功率化、数字化和实用化。

［1］周志敏，周纪海，纪爱华.开关电源功率因数校正电路设计与应用［M］.北京:人民邮电出版社，2004.

［2］李凯旋.60kwPWM整流器研究［M］.北京:北京交通大学，2009.

［3］刘小刚，彭卫东，张鹏飞.大功率三相APFC技术研究现状及发展趋势［J］.电子技术，2010，47(9):14-16.

［4］方宇.三相PFC及其数字控制.南京:南京航空航天大学，2004.

［5］Rui Li，Ke Ma，Dehong Xu.A Novel 40KW ZVS-SVM Controlled Three-Phase Boost PFC Converter.Applied Power Electronics Conference and Exposition，Feb，2009:376-382.

［6］王万宝.三相电压型 SVPWM整流器仿真研究［M］.重庆:重庆大学，2009.

［7］李荣华，王桂华.基于dq坐标的三相VSR建模与解耦分析［J］.电气开关，2009，03:23-25.

［8］刘新伟.馈能型三相PWM整流器的研究［M］.杭州:浙江大学，2008.

［9］刘念洲，刘成浩.基于MATLAB的三相电压型PWM整流系统仿真［J］.航电技术，2009，29(02):43-46.

［10］Nobuhito Takeuchi，Keiju Matsui，IsamuYamamoto，Masaru Hasegawa，Fukashi Veda，Hideki Mori.A Novel PFC Circuit for Three-Phase utilizing a Single Switching Device.Telecommunications Energy Conference，Sept，2008:1-5.

［11］白志范，沈跃，等.动态负载下无差拍SVPWM调制弧焊电源三相 PFC［J］.吉林大学学报(工学版)，2009，39(2):306-310.

［12］Jun-Ichi Itoh，Member，IEEE，and Itsuki Ashida.A Novel Three-Phase PFC Rectifier Using a Harmonic Current Injection Method.IEEE Trans.Power Electron，2008，23(2):715-722，