基于突变-可拓学的港口物流绩效双层评价模型

辛曼玉

(东莞职业技术学院物流工程系，广东东莞 5 23808)

0 引言

经济全球化的发展和国际贸易量的不断增加使得港口在国民经济和全球物流供应链中的地位不断提升，其发展潜力巨大.但在面临良好发展机遇的同时也面临着众多的困难和挑战，港口物流企业必须不断提高物流服务水平、提升综合竞争力.［1]港口物流绩效即是对港口物流经济能力、社会能力、环境和资源能力的衡量.在发展港口物流的同时，进行港口物流绩效评价，对港口自身物流系统的完善、经营能力和整体效益的增加，有着非常重要的意义.［2]

目前，国内常用的绩效评价方法有层次分析法、主成分分析法、模糊数学评判法以及数据包络分析法等.用层次分析法无论是建立层次结构还是构造判断矩阵，人的主观因素对评价结果的影响极大;模糊数学法强调极值作用，在权重赋值上具有较大的主观随意性，评价精度一般较低;数据包络分析法能克服一定的主观性，但其数学意义过于高深，实际操作难度很大.突变级数法虽然没有对指标采用权重，但它考虑到各评价指标的相对重要性，从而既减少主观性又不失科学性.［3]可拓学是研究事物拓展的可能性和开拓创新的规律与方法，并用以解决矛盾问题，其揭示事物内部的规律与因素，并能有效处理初始数据.［4]

针对国内港口物流系统发展的实际情况，在数据可得性基础上，本文从物流硬件水平、物流管理与服务水平以及港口物流对社会的贡献率等3个方面建立评价指标体系，并首次将突变级数法与可拓学相结合建立双层决策系统模型.该模型克服各自方法的局限性，提高计算结果的精确度，使评价结果更具有客观性和可靠性.

1 港口物流绩效评价体系的建立

焦新龙等［5]根据Delphi及AHP法构建基于硬件水平、经营管理水平和客户满意度等3个方面共21个二级指标的港口物流绩效综合评价体系;王玖河等［6]从财务、物流作业、客户服务和员工素质等4个角度设计共24个二级指标的港口物流绩效评价指标体系;刘秀国等［7]从可持续发展的角度对港口物流绩效的预警进行研究，并从港口物流经济水平等3个方面建立评价指标体系.在科学性、系统性、通用可比性以及实用性原则的基础上，借鉴前人研究成果并充分考虑数据可得性的前提下，构建新的评价指标体系，分别从港口的物流硬件水平、物流管理与服务水平、港口物流对社会的贡献率等3个方面作出评价，指标体系见表1.

表1 港口物流绩效评价体系

2 基于突变-可拓学的双层决策系统模型建立

突变级数法和可拓学理论已被广泛应用于综合评价研究中.突变级数法是对评价目标进行多层次矛盾分解，然后将突变理论与模糊数学相结合产生突变模糊隶属函数，从而对评价目标进行排序分析的一种综合评价方法.张勇［8]利用突变理论对绩效评价进行初步探索，并建立基于突变级数法的绿色供应链管理绩效评价模型;丁琳［9]认为突变级数法需要在同一层次的指标上区分指标的重要程度，增加指标设计的难度和评价的主观性，因此运用主成分分析法进行辅助评价.可拓学是研究事物拓展的可能性和开拓创新的规律与方法，用以解决矛盾问题.胡启洲等［10]利用可拓学中的物元分析理论和信息论中的熵理论对城市公交系统的发展进行定量研究，其提出的复合物元模型为多层次多目标测定问题提供一种合理可行的方法.将突变级数法与可拓学相结合并建立双层决策系统模型，既能克服各自方法的局限性，又能提高计算结果的精确度，增加评价的客观性和可靠性.因此，本文采用突变-可拓学双层决策模型对港口物流绩效进行评价研究.

2.1 基于可拓学的下层子决策系统分析模型

2.1.1 下层可拓学子系统决策矩阵标准化及方案指标距离矩阵的建立

A总体评价体系下有i个子系统，其中将第i个子系统记为Bi.对Bi子系统进行优化调整，设有n个待决策的可选择方案，记为，i=1，2，3}，而各个子系统有数量不等的目标函数，其中第i个子系统Bi具有m(i)个目标函数作为指标集，记作.方案 Bi对指标中第k个方案第j个目标函数的属性值为，则矩阵表示方案集对指标集的决策矩阵.因此，方案Bi的决策矩阵用可拓学分析矩阵表示为

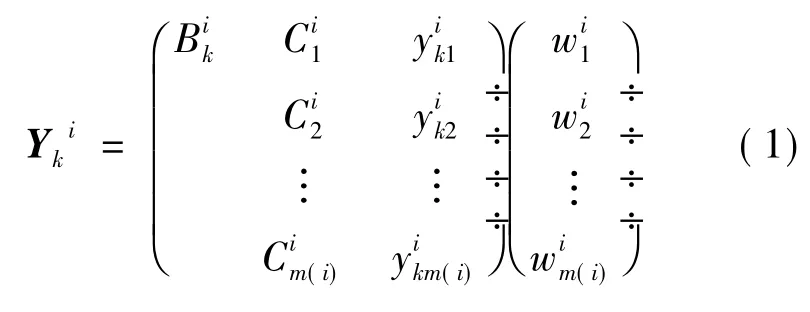
由于m个优化目标的含义和计算方法不同，以至于它们的量纲各异，对决策矩阵进行标准化处理.令J+={越大越好的指标}，J－={越小越好的指标}，则有

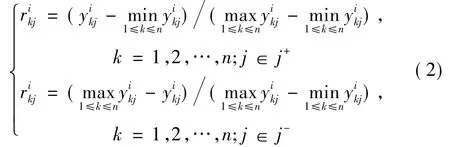
标准化处理后的方案Bik的标准决策矩阵为

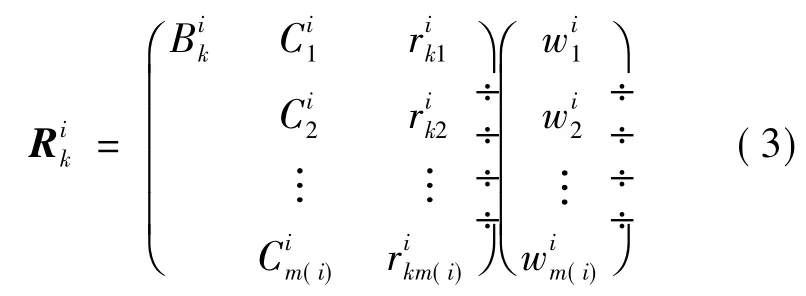
令

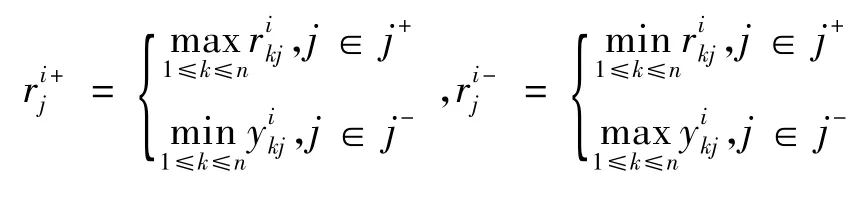
则Bi子评价系统的正负理想方案指标矩阵分别为

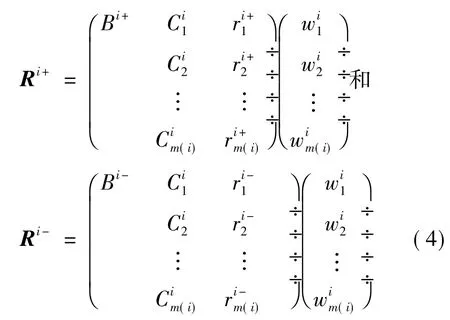
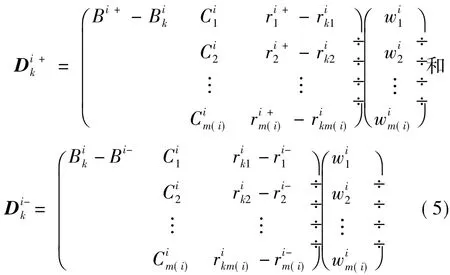
2.1.2 确定目标函数的熵权系数

在权重的确定方面，采用熵权系数法，其中第j个目标函数的熵为

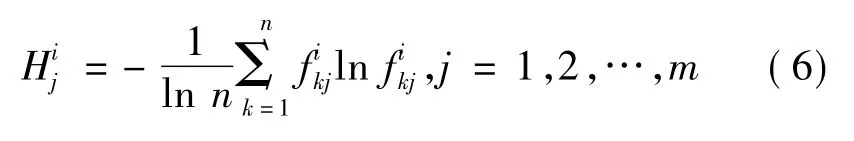
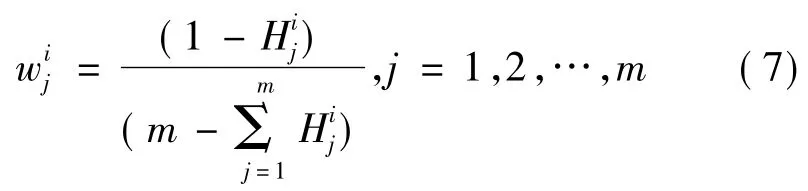
即m个目标函数的权重向量:

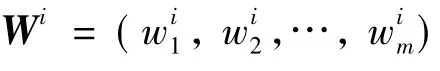
2.1.3 下层可拓学子系统决策模型

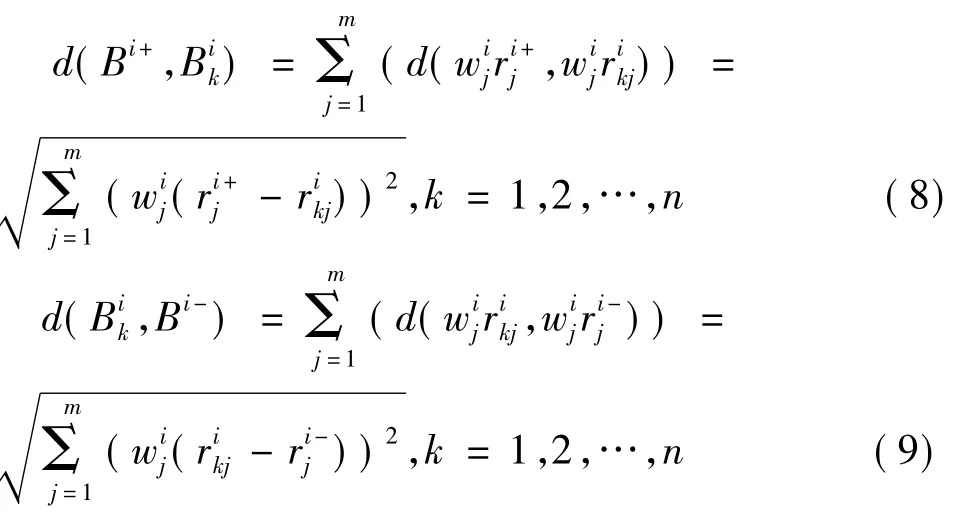
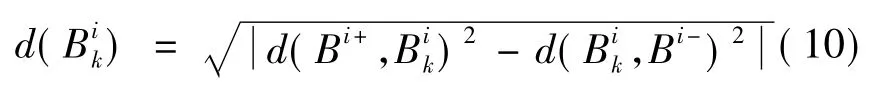
由此，可分别得到第k个方案的各子系统综合决策值所组成的子决策向量D(Bk)=(d()，d()，d())，即方案k的下层系统决策评价向量为D(Bk)=(d()，d()，d())

2.2 基于突变级数的上层决策系统评价

在上层模型中，将方案的总决策作为状态变量，将每个子系统的综合决策值作为控制变量，并采用燕尾突变模型对各方案的上层决策值进行测算.其中，燕尾突变模型归一公式为

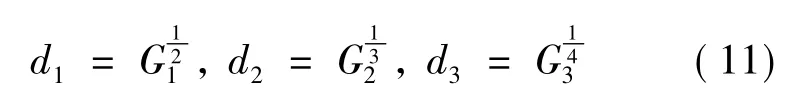
结合以上理论，上层决策系统评价的步骤:

(1)将2.1.2中的熵权系数法扩展到整个评价体系，求出下层模型中各指标占整个体系的权重，以求得下层各子系统占整个体系的权重，并按权重从大到小的顺序对子系统进行排序，依次对应排列综合决策值，得出新的决策向量:Gk=(Gk1，Gk2，Gk3).

(2)运用燕尾突变模型归一公式，对Gk进行计算，即

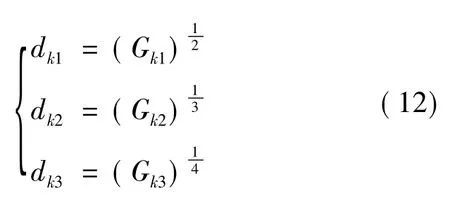
(3)对燕尾归一模型所得值按互补原则计算，可得k方案的整体综合决策值，即

从而得出方案决策集 D={dk1，dk2，dk3}.

(4)按照D对方案进行排序，以得到最佳方案.由于下层模型中应用可拓学分析模型求得子系统的决策值，其实质为欧几里德距离，则其决策值越小，方案越优.

3 模型的实例应用

下面应用港口物流绩效评价模型，对我国7个沿海港口2005年的港口物流绩效进行评价.根据2005年各港口统计年鉴的资料查询以及专家打分，2005年7个港口的物流绩效评价结果见表2.

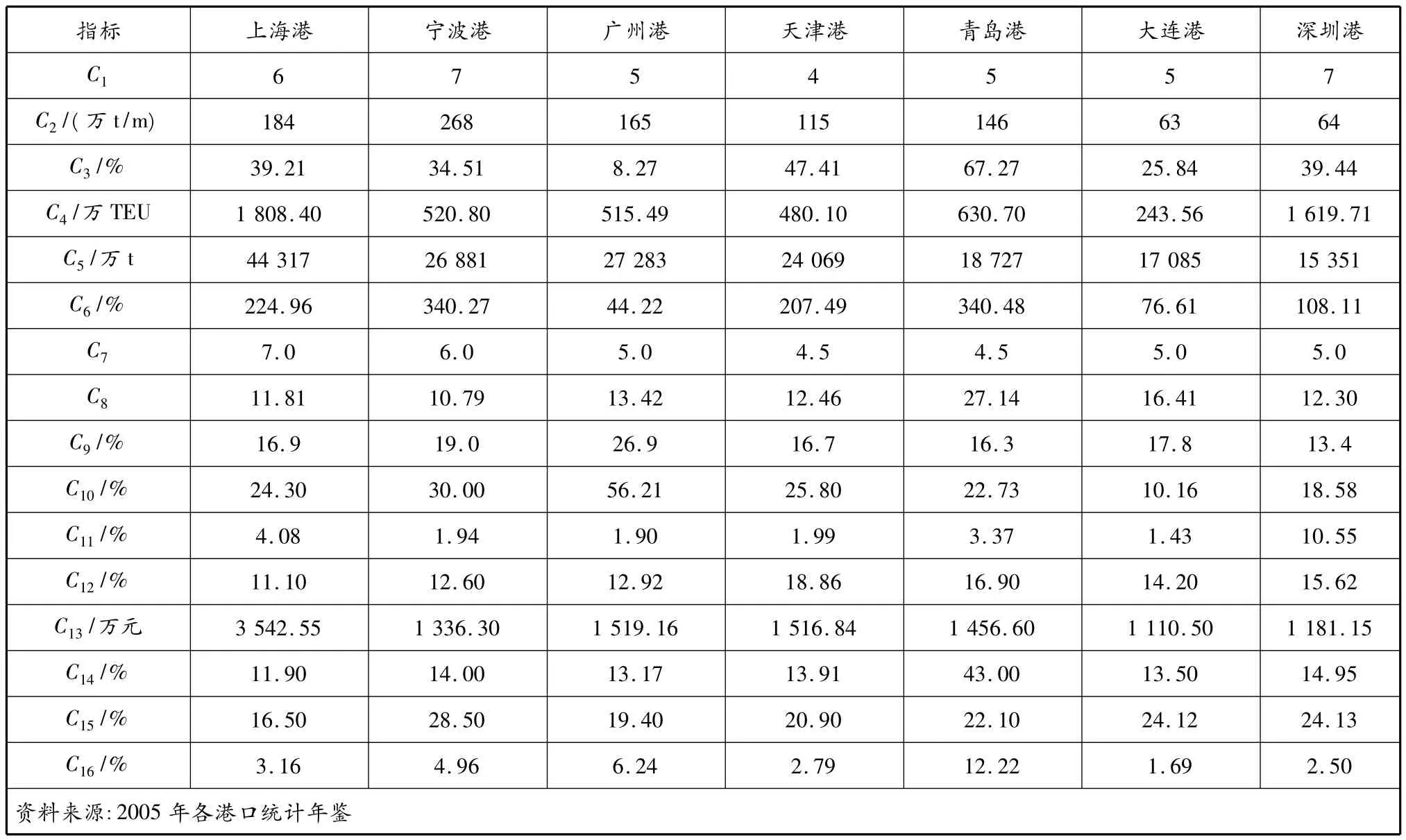
表2 7个沿海港口2005年物流绩效评价结果

(1)下层可拓学子系统决策.以上海港决策子系统B1为例，通过对上海港物流经济水平子系统进行评价计算来阐述下层模型的计算.

用式(1)～(3)求得上海港的方案决策矩阵

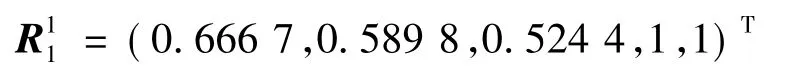
根据公式(4)和(5)可分别求得上海港的子系统B1的正负理想方案指标矩阵

因此，根据式(8)和(9)可求得上海港的子系统B1的正负理想方案指标矩阵

由式(6)和(7)可得子系统B1的各指标权重向量为

综合以上结果，根据式(10)，可以求得上海港的决策子系统B1的决策值为

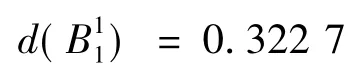
同理，可求得上海港其他决策子系统的决策值，以及其他港口的下层模型决策值，计算结果见表3.

表3 下层模型决策值计算结果

(2)上层突变级数模型.根据式(6)和(7)可求得各子系统在整个决策系统中的熵权值

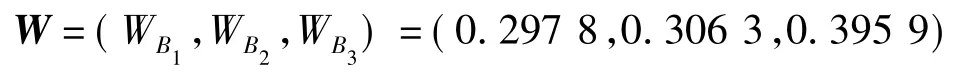
由此重新排列上层决策变量值

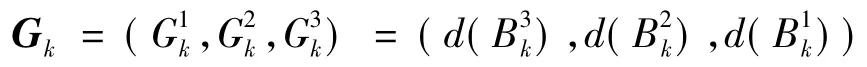
再根据式(12)和(13)，可求得各港口的上层决策值.各港口上层决策值及优劣排序见表4.

表4 上层决策值及优劣排序表

由表4可见，在港口物流绩效评价中上海港排名第一，青岛港第二，接下去依次是广州港、深圳港、宁波港、天津港和大连港.这与我国2005年港口的综合排名基本符合.上海港的物流硬件水平、物流管理与服务水平、港口物流对社会的贡献率等3个指标都处于领先地位，其次为青岛港和广州港.该评价结果与这几个港的实际发展情况比较符合，可说明该决策评价方法的适用性与可靠性.

4 结束语

高水平的港口物流绩效是港口竞争力的有效支撑，现代物流已成为港口经济新的增长点［11].本文从物流硬件水平、物流管理与服务水平以及港口物流对社会的贡献率等3个维度出发建立针对港口物流的评价体系，并对其下层指标尽量采用数据可取的指标;在评价权重确定上采用基于突变-可拓学的双层评价模型，既综合突变理论的运算简单与结果合理，又结合可拓学的揭露数据之间逻辑特性的特点，克服以往评价方法主观性太强的缺点.此外，通过实例论证，此方法具有较高的实用性.

［1]刘秀国.基于可持续发展的港口物流绩效评价及预警研究［D].天津:天津大学，2009.

［2]姜超雁，真虹，高洁.基于模糊综合评价法的中小型第三方物流企业绩效评价［J].上海海事大学学报，2011，32(1):86-90.

［3]李振福，杨忠振.模糊可拓层次分析法研究［J].上海海事大学学报，2006，27(3):71-75.

［4]蔡文，杨春燕，何斌.可拓学基础理论研究的新进展［J].中国工程科学，2003，5(2):81-85.

［5]焦新龙，刘雪莲，马天山.港口物流绩效定量评价理论及应用［J].经济地理，2009，29(12):2034-2038.

［6]王玖河，白满元.基于BSC和PCA的港口物流绩效评价［J].技术与创新管理，2010，31(4):416-418.

［7]刘秀国，何桢.基于可持续发展的港口物流绩效预警研究［J].西安电子科技大学学报，2009，19(4):54-58.

［8]张勇.基于突变理论的绿色供应链绩效评价研究［D].哈尔滨:哈尔滨工程大学，2008.

［9]丁琳.基于突变级数法的中小企业成长性评价研究［D].济南:山东大学，2010.

［10]胡启洲，陆化普.基于关联熵与复合物元的公交系统综合测度模型［J].系统工程理论与实践，2011，31(1):186-192.

［11]曹坤.物流企业的绩效评价体系和评价方法［J].上海海事大学学报，2006，27(4):106-111.