小波包变换和能量分析在声发射信号降噪中的应用

付元杰

(浙江省特种设备检验研究院,杭州 310020)

材料或结构在受外力或内力作用产生变形或断裂时,会以弹性波的形式快速释放出应变能,这一现象称为声发射。声发射信号具有瞬态性和随机性,属于非平稳的随机信号。声发射的产生是由于材料内部结构的相对运动导致的,通过传感器接收到的应力波正是这种相对运动的反映,它包含了关于材料内部运动的几乎全部的信息。在对材料受力过程中内部变换状态的研究中,因为无法直接得到这种内部的运动状态,因此可以通过分析传感器接收到的这一过程中产生的声发射信号来反推。反推的困难在于直接接收的信号成分的复杂性,不能得到纯正的结构运动的声发射信号,这些重要的信号往往在采集的过程中遭到强大噪声的污染。如何从传感器得到的信号中提取内部结构运动的信息,是材料结构研究需要解决的重要课题。声发射信号的能量和频率成分反映了内部结构运动的剧烈程度和能量释放的快慢。小波包变换是目前非平稳信号分析最有力的工具之一,其特点是对信号进行变时窗分析,即采用不同宽度的时窗分析信号的低频和高频部分。这个特点使得小波包在时域和频域同时具有良好的局部分析特性。笔者尝试运用小波包变换的频率分解功能,结合能量计算的方法,对采集到的声发射信号进行降噪,提取纯正有用的结构变化信号。试验证明该方法行之有效。

1 小波包变换原理[1-2]

设函数 Ψ(t)∈L1∩L2,如果满足：

则称 Ψ(t)为一个基本小波或小波母函数,式中˜Ψ(ω)为函数 Ψ(t)的傅里叶变换,因此上式被称为可容许性条件。令：

式中a,b∈R,a≠0,此式被称为基本小波或小波母函数。Ψ(t)是依赖a,b生成的小波,a被称为尺度因子,b被称为平移参数。尺度因子改变连续小波的形状,平移参数改变小波的位移。

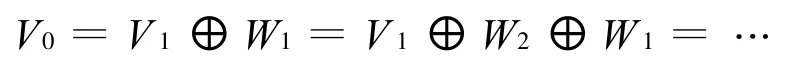
随着尺度因子a的减小,小波 Ψa,b(t)的时宽变宽,˜Ψa,b(ω)的带宽增大。从多分辨率分析的角度来看：只是对V空间迭代进行分解的结果,表明多分辨率分析是按照不同的尺度因子j把希尔伯特空间分析为所有子空间Wj的正交和,其中Wj为小波函数 Ψ(t)的子空间。从此对小波子空间Wj按照二进制方式进行频率的细分,可以达到提高频率分辨率的目的。首先将尺度子空间Vj和小波子空间Wj用一个新的子空间表示,令：

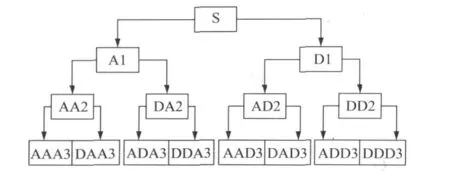
图1 三层小波包分解树示意图

则希尔伯特空间的正交分解Vj+1=Vj⊕Wj可用Unj的分解系统一起来,并把这种表示方法推广到n∈Z+。小波包分解的示意图见图1,他是将每一层所得子带均一分为二,并传至下一层。可以看出,每一层的子带都覆盖信号所占有的频率,只是各层的分辨率不同。因此,利用小波包分解多少层,以及各层选择哪些子带来进行分析,即对不同的信号,应该选择相应的“最佳”滤波器。

小波包的重构算法为：

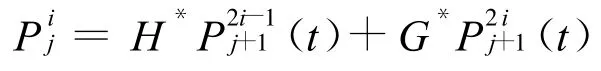
式中j=J-1,J-2,…,1,0;i=2j,2j-1,…,2,1;H*和G*分别为H和G的对偶算子。

2 声发射信号的小波包变换及能量分析降噪特性

小波包变换是从小波变换的基础上发展而来的。从工程技术上看,小波包变换可以看成是函数空间逐级正交剖分的扩展,能够为信号分析提供一种更加精细的分析方法。它将频带进行多层次划分,对多分辨率分析没有细分的高频部分进一步分解,并可以一直分解下去。图1中信号经过三层小波包分解后形成了若干个信号包,应用时根据需要的信号段,可以选择不同的信号包来部分重构原始信号。

声发射信号是能量突然释放的产物,虽然信号从产生到被接收的过程中要发生模式的转变,得不到真实的源信号,但是传感器接收到的信号同声发射源信号有着对应的频率和能量关系。能量和频率是声发射源的重要特征值,分别反映了结构变化的剧烈程度和能量释放的快慢。在声发射信号分析时,先对信号进行一定尺度上的小波包分解;将每个分解后的信号包进行单独重构,计算其频谱,分析每个分解包上信号的详细频谱情况;计算各尺度信号的能量和各尺度信号能量占信号总能量的比值(能量系数);根据声发射信号的先验知识、噪声的频率范围和各尺度的能量比值,舍弃能量比重小的信号包,对剩余信号包进行重构,可得到声发射信号的特征信号,从而提高信噪比。

3 小波包分解及能量分析在声发射信号降噪中的应用[3]

以金属材料Q235试件拉伸试验中采集到的一段裂纹声发射信号为例,金属材料声发射信号频率主要集中在100～300 k Hz。该信号的采样频率为625 k Hz,采样点数为2 048点,其时域波形如图2。从时域图上可以看出,声发射信号在1 000点以前幅值较高,1000点之后基本上已经衰减到0值。除此之外,难以得到频率和能量的明显关系。若将信号引入到小波包空间,则能使信号的细部特征清晰地呈现出来。

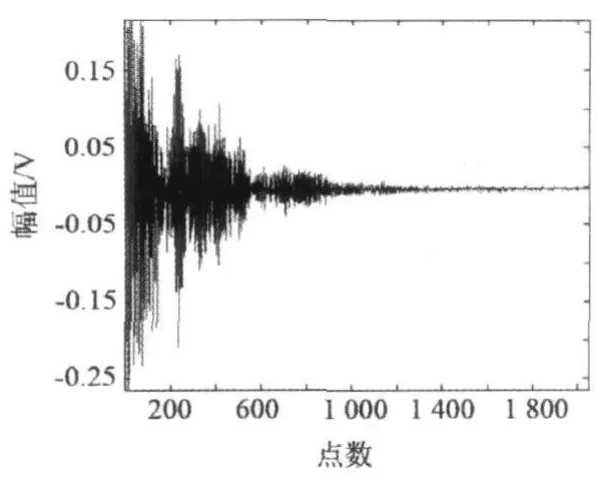
图2 裂纹声发射信号时域图

根据以往的研究经验[4],采用 sym8小波函数对图2中的声发射信号进行4个尺度的小波包分解,分解树结构见图3。各尺度分解的重构波形信号及其对应的频谱见图4。

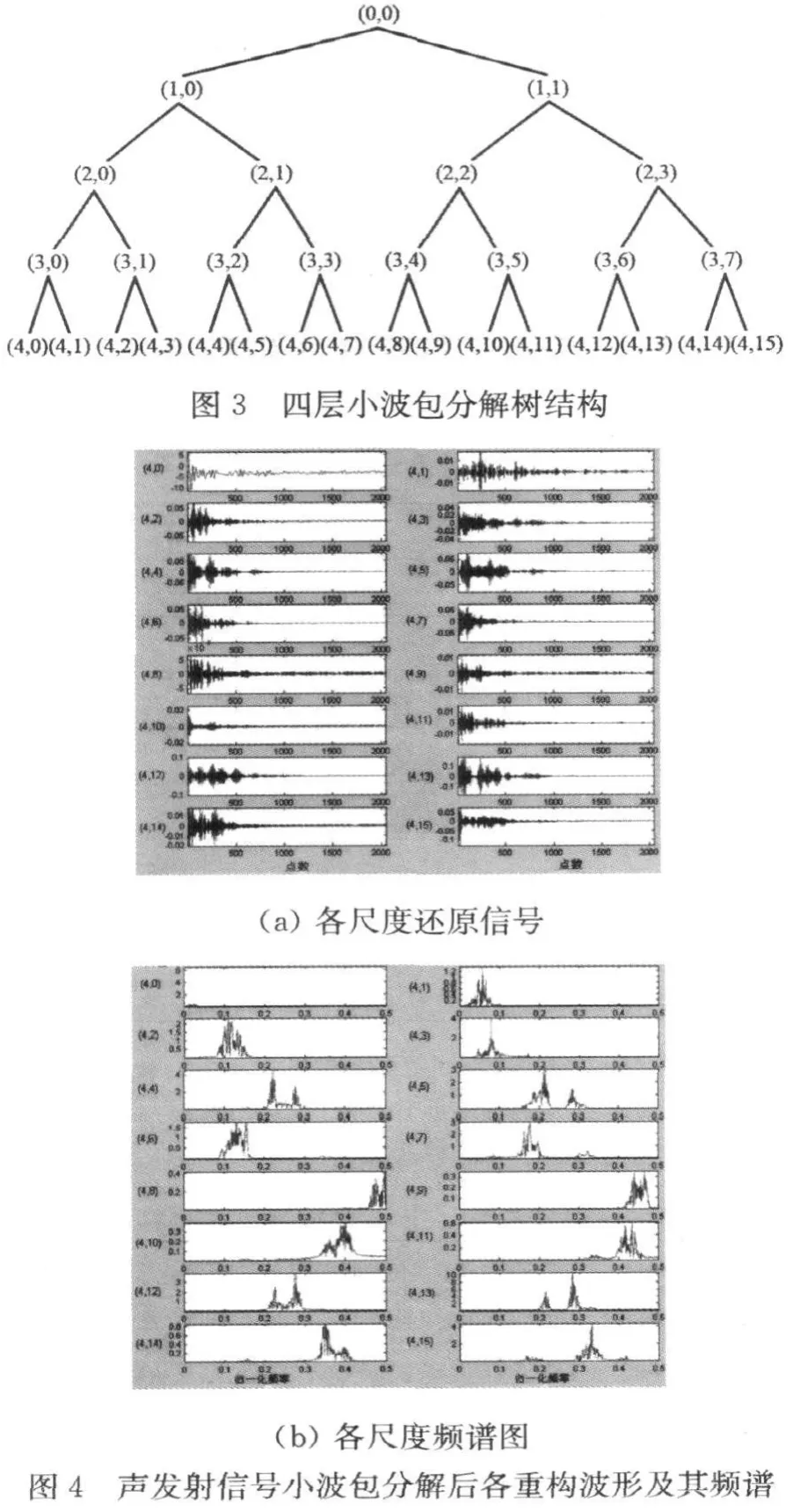
小波包分解各层的能量同总能量的比值见表1。将各层能量比值存入能量系数向量,E={Ei},i=1,2,3,…,16,其直方图如图5。

表1 节点能量比值

图5 能量系数直方图

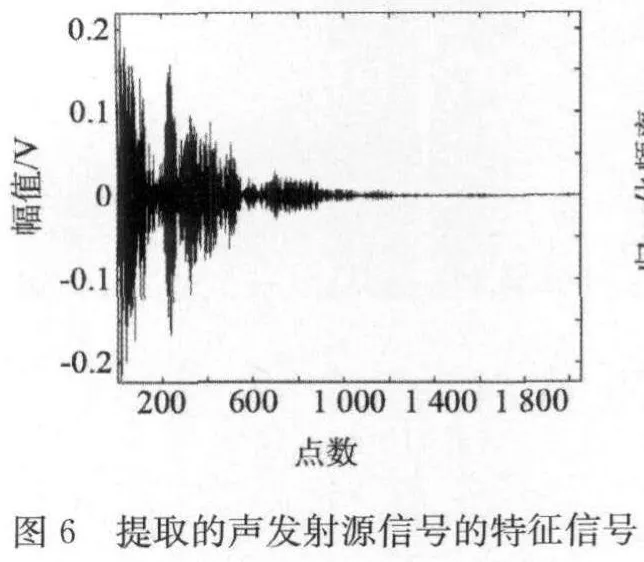
由频谱图4可以看出,节点(4,0),(4,1),(4,2),(4,3)和(4,6)的信号频率都在100 k Hz以下,不在金属材料声发射信号频率范围之内,可以当作噪声舍弃。另外,节点(4,8),(4,9),(4,10),(4,11)和(4,14)信号能量占总能量的比例都＜1%,同样可当作噪声舍弃。剩下几个节点的能量占到总能量的77.143%。将这几个节点信号进行组合得到该列信号中的特征信号,还原到时域后得图6。还原信号与原来信号的方差为6.3154×10-13。原始声发射信号时频图如图7,提取特征频率后还原信号的时频图如图8。

4 结论

小波包变换可以方便地将声发射信号分解到不同的频率段,计算不同频率段信号的能量。将小能量的频段信号舍弃后重构信号,得到的信号保留了原来信号的主要特征,同时复杂的信号也得到了简化和过滤,为声发射信号的后续处理提供了可靠的输入数据。

[1]程正兴.小波分析算法与应用[M].西安：西安交通大学出版社,1998.

[2]孙晓兵,保铮.基于时频域相关能量的时变信号分析[J].西安电子科技大学学报,1996,23(2)：137-144.

[3]付元杰,毛汉领,黄振峰,等.特征声发射信号的时频能量分析[J].装备制造技术,2006(2)：27-29.

[4]张平.声发射检测信号的信号处理方法[D].北京：清华大学,2000.